
Wittgenstein's rod is a problem in geometry discussed by 20th-century philosopher Ludwig Wittgenstein.

Wittgenstein's rod is a problem in geometry discussed by 20th-century philosopher Ludwig Wittgenstein.
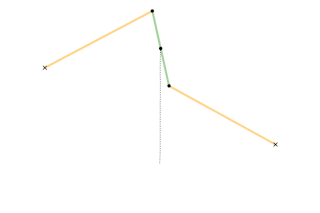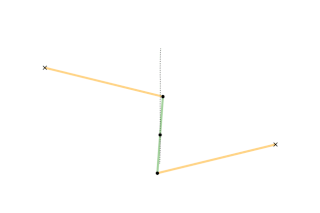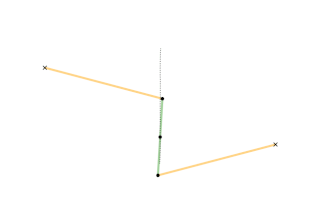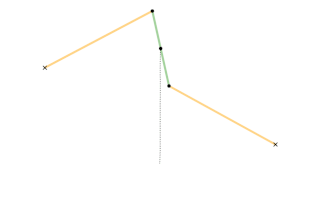
A ray is drawn with its origin A on a circle, through an external point S and a point B is chosen at some constant distance from the starting end of the ray; what figure does B describe when all the initial points on the circle are considered? The answer depends on three parameters: the radius of the circle, the distance from the center to S, and the length of the segment AB. The shape described by B can be seen as a 'figure-eight' which in some cases degenerates to a single lobe looking like an inverted cardioid.
If B remains on the same side of S with respect to the center of the circle, instead of a ray one can consider just a segment or the rod AB.
Wittgenstein sketched a mechanism and wrote:
While the point A describes a circle, B describes a figure eight. Now we write this down as a proposition of kinematics.
When I work the mechanism its movement proves the proposition to me; as would a construction on paper.
The proposition corresponds e.g. to a picture of the mechanism with the paths of the points A and B drawn in. Thus it is in a certain respect a picture of that movement. It holds fast what the proof shows me. Or – what it persuades me of.
This text has been included among the notes selected for publication in Remarks on the Foundations of Mathematics and the editors have dated in the as spring of 1944. [1]
Wittgenstein's rod is a generalization of Hoeckens linkage.

Archimedes of Syracuse was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Considered the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.

A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius.

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.

Ludwig Josef Johann Wittgenstein was an Austrian philosopher who worked primarily in logic, the philosophy of mathematics, the philosophy of mind, and the philosophy of language.

The Tractatus Logico-Philosophicus is the only book-length philosophical work by the Austrian philosopher Ludwig Wittgenstein that was published during his lifetime. The project had a broad goal: to identify the relationship between language and reality and to define the limits of science. Wittgenstein wrote the notes for the Tractatus while he was a soldier during World War I and completed it during a military leave in the summer of 1918. It was originally published in German in 1921 as Logisch-Philosophische Abhandlung. In 1922 it was published together with an English translation and a Latin title, which was suggested by G. E. Moore as homage to Baruch Spinoza's Tractatus Theologico-Politicus (1670).
Frank Plumpton Ramsey was a British philosopher, mathematician, and economist who made major contributions to all three fields before his death at the age of 26. He was a close friend of Ludwig Wittgenstein and, as an undergraduate, translated Wittgenstein's Tractatus Logico-Philosophicus into English. He was also influential in persuading Wittgenstein to return to philosophy and Cambridge. Like Wittgenstein, he was a member of the Cambridge Apostles, the secret intellectual society, from 1921.

Apollonius of Perga was an ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the earlier contributions of Euclid and Archimedes on the topic, he brought them to the state prior to the invention of analytic geometry. His definitions of the terms ellipse, parabola, and hyperbola are the ones in use today. With his predecessors Euclid and Archimedes, Apollonius is generally considered among the greatest mathematicians of antiquity.

In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ∠ ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

In geometry, a locus is a set of all points, whose location satisfies or is determined by one or more specified conditions.

Logical atomism is a philosophical view that originated in the early 20th century with the development of analytic philosophy. It holds that the world consists of ultimate logical "facts" that cannot be broken down any further, each of which can be understood independently of other facts.

In geometry, an arbelos is a plane region bounded by three semicircles with three apexes such that each corner of each semicircle is shared with one of the others (connected), all on the same side of a straight line that contains their diameters.

In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points.

In kinematics, the parallel motion linkage is a six-bar mechanical linkage invented by the Scottish engineer James Watt in 1784 for the double-acting Watt steam engine. It allows a rod moving practically straight up and down to transmit motion to a beam moving in an arc, without putting significant sideways strain on the rod.
In kinematics, Watt's linkage is a type of mechanical linkage invented by James Watt in which the central moving point of the linkage is constrained to travel on a nearly straight line. It was described in Watt's patent specification of 1784 for the Watt steam engine.

A pressure–volume diagram is used to describe corresponding changes in volume and pressure in a system. They are commonly used in thermodynamics, cardiovascular physiology, and respiratory physiology.
The axiom of reducibility was introduced by Bertrand Russell in the early 20th century as part of his ramified theory of types. Russell devised and introduced the axiom in an attempt to manage the contradictions he had discovered in his analysis of set theory.

The Book of Lemmas or Book of Assumptions is a book attributed to Archimedes by Thābit ibn Qurra, though the authorship of the book is questionable. It consists of fifteen propositions (lemmas) on circles.
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.

A trammel of Archimedes is a mechanism that generates the shape of an ellipse. It consists of two shuttles which are confined ("trammeled") to perpendicular channels or rails and a rod which is attached to the shuttles by pivots at fixed positions along the rod.

Remarks on the Foundations of Mathematics is a book of Ludwig Wittgenstein's notes on the philosophy of mathematics. It has been translated from German to English by G.E.M. Anscombe, edited by G.H. von Wright and Rush Rhees, and published first in 1956. The text has been produced from passages in various sources by selection and editing. The notes have been written during the years 1937–1944 and a few passages are incorporated in the Philosophical Investigations which were composed later. When the book appeared it received many negative reviews mostly from working logicians and mathematicians, among them Michael Dummett, Paul Bernays, and Georg Kreisel. Today Remarks on the Foundations of Mathematics is read mostly by philosophers sympathetic to Wittgenstein and they tend to adopt a more positive stance.