Related Research Articles

The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves. It is Turing complete and can simulate a universal constructor or any other Turing machine.

A cellular automaton is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling.

The Rule 110 cellular automaton is an elementary cellular automaton with interesting behavior on the boundary between stability and chaos. In this respect, it is similar to Conway's Game of Life. Like Life, Rule 110 with a particular repeating background pattern is known to be Turing complete. This implies that, in principle, any calculation or computer program can be simulated using this automaton.
A cellular automaton (CA) is Life-like if it meets the following criteria:

Seeds is a cellular automaton in the same family as the Game of Life, initially investigated by Brian Silverman and named by Mirek Wójtowicz. It consists of an infinite two-dimensional grid of cells, each of which may be in one of two states: on or off. Each cell is considered to have eight neighbors, as in Life. In each time step, a cell turns on or is "born" if it was off or "dead" but had exactly two neighbors that were on; all other cells turn off. Thus, in the notation describing the family of cellular automata containing Life, it is described by the rule B2/S.

In a cellular automaton, a Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configurations after the Garden of Eden in Abrahamic religions, which was created out of nowhere.

A second-order cellular automaton is a type of reversible cellular automaton (CA) invented by Edward Fredkin where the state of a cell at time t depends not only on its neighborhood at time t − 1, but also on its state at time t − 2.

A block cellular automaton or partitioning cellular automaton is a special kind of cellular automaton in which the lattice of cells is divided into non-overlapping blocks and the transition rule is applied to a whole block at a time rather than a single cell. Block cellular automata are useful for simulations of physical quantities, because it is straightforward to choose transition rules that obey physical constraints such as reversibility and conservation laws.

Rule 30 is an elementary cellular automaton introduced by Stephen Wolfram in 1983. Using Wolfram's classification scheme, Rule 30 is a Class III rule, displaying aperiodic, chaotic behaviour.

A cyclic cellular automaton is a kind of cellular automaton rule developed by David Griffeath and studied by several other cellular automaton researchers. In this system, each cell remains unchanged until some neighboring cell has a modular value exactly one unit larger than that of the cell itself, at which point it copies its neighbor's value. One-dimensional cyclic cellular automata can be interpreted as systems of interacting particles, while cyclic cellular automata in higher dimensions exhibit complex spiraling behavior.

In cellular automata, the von Neumann neighborhood is classically defined on a two-dimensional square lattice and is composed of a central cell and its four adjacent cells. The neighborhood is named after John von Neumann, who used it to define the von Neumann cellular automaton and the von Neumann universal constructor within it. It is one of the two most commonly used neighborhood types for two-dimensional cellular automata, the other one being the Moore neighborhood.
The majority problem, or density classification task, is the problem of finding one-dimensional cellular automaton rules that accurately perform majority voting.

Rule 184 is a one-dimensional binary cellular automaton rule, notable for solving the majority problem as well as for its ability to simultaneously describe several, seemingly quite different, particle systems:

Lattice gas automata (LGCA), or lattice gas cellular automata, are a type of cellular automaton used to simulate fluid flows, pioneered by Hardy–Pomeau–de Pazzis and Frisch–Hasslacher–Pomeau. They were the precursor to the lattice Boltzmann methods. From lattice gas automata, it is possible to derive the macroscopic Navier–Stokes equations. Interest in lattice gas automaton methods levelled off in the early 1990s, as the interest in the lattice Boltzmann started to rise. However, an LGCA variant, termed BIO-LGCA, is still widely used to model collective migration in biology.

In the mathematical study of cellular automata, Rule 90 is an elementary cellular automaton based on the exclusive or function. It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value. In each time step all values are simultaneously replaced by the exclusive or of their two neighboring values. Martin, Odlyzko & Wolfram (1984) call it "the simplest non-trivial cellular automaton", and it is described extensively in Stephen Wolfram's 2002 book A New Kind of Science.
The Curtis–Hedlund–Lyndon theorem is a mathematical characterization of cellular automata in terms of their symbolic dynamics. It is named after Morton L. Curtis, Gustav A. Hedlund, and Roger Lyndon; in his 1969 paper stating the theorem, Hedlund credited Curtis and Lyndon as co-discoverers. It has been called "one of the fundamental results in symbolic dynamics".
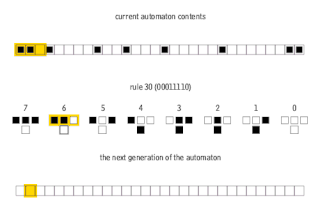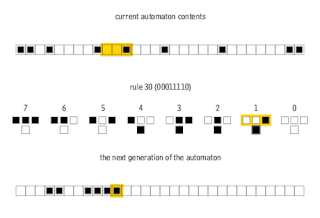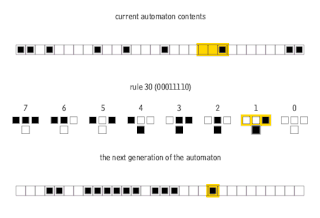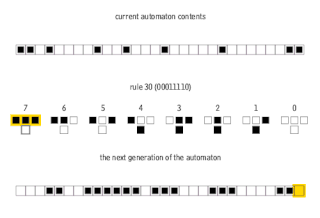
In mathematics and computability theory, an elementary cellular automaton is a one-dimensional cellular automaton where there are two possible states and the rule to determine the state of a cell in the next generation depends only on the current state of the cell and its two immediate neighbors. There is an elementary cellular automaton which is capable of universal computation, and as such it is one of the simplest possible models of computation.

Life without Death is a cellular automaton, similar to Conway's Game of Life and other Life-like cellular automaton rules. In this cellular automaton, an initial seed pattern grows according to the same rule as in Conway's Game of Life; however, unlike Life, patterns never shrink. The rule was originally considered by Toffoli & Margolus (1987), who called it "Inkspot"; it has also been called "Flakes". In contrast to the more complex patterns that exist within Conway's Game of Life, Life without Death commonly features still life patterns, in which no change occurs, and ladder patterns, that grow in a straight line.

A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.
In mathematics, a surjunctive group is a group such that every injective cellular automaton with the group elements as its cells is also surjective. Surjunctive groups were introduced by Gottschalk (1973). It is unknown whether every group is surjunctive.
References
- ↑ Ceccherini-Silberstein, Tullio; Coornaert, Michel (2010). Cellular Automata and Groups. Springer. p. 28. doi:10.1007/978-3-642-14034-1. ISBN 978-3-642-14034-1 . Retrieved 22 October 2022.
- ↑ Wolfram, Stephen (July 1983). "Statistical Mechanics of Cellular Automata". Reviews of Modern Physics. 55 (3): 601–644. Bibcode:1983RvMP...55..601W. doi:10.1103/RevModPhys.55.601.
- ↑ Wolfram, Stephen (May 14, 2002). A New Kind of Science. Wolfram Media, Inc. ISBN 1-57955-008-8.