
A circle is a simple closed shape. It is the set of all points in a plane that are at a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves so that its distance from a given point is constant. The distance between any of the points and the centre is called the radius. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.
In hyperbolic geometry, the ultraparallel theorem states that every pair of ultraparallel lines has a unique common perpendicular hyperbolic line.

In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle O of radius r is defined by.

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga posed and solved this famous problem in his work Ἐπαφαί ; this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets.

In hyperbolic geometry, a horocycle is a curve whose normal or perpendicular geodesics all converge asymptotically in the same direction. It is the two-dimensional example of a horosphere.
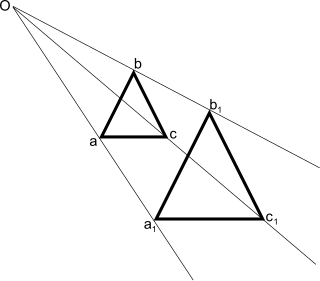
In geometry, a homothetic center is a point from which at least two geometrically similar figures can be seen as a dilation or contraction of one another. If the center is external, the two figures are directly similar to one another; their angles have the same rotational sense. If the center is internal, the two figures are scaled mirror images of one another; their angles have the opposite sense.
In Euclidean geometry, Apollonius' problem is to construct all the circles that are tangent to three given circles. Special cases of Apollonius' problem are those in which at least one of the given circles is a point or line, i.e., is a circle of zero or infinite radius. The nine types of such limiting cases of Apollonius' problem are to construct the circles tangent to:
- three points
- three lines
- one line and two points
- two lines and a point
- one circle and two points
- one circle, one line, and a point
- two circles and a point
- one circle and two lines
- two circles and a line
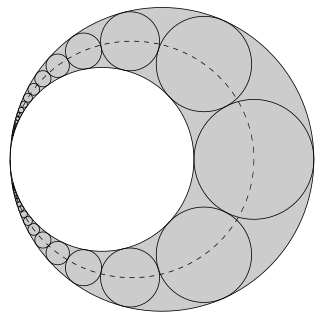
In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD.

In geometry, the Bankoff circle or Bankoff triplet circle is a certain Archimedean circle that can be constructed from an arbelos; an Archimedean circle is any circle with area equal to each of Archimedes' twin circles. The Bankoff circle was first constructed by Leon Bankoff.

In geometry, the twin circles are two special circles associated with an arbelos. An arbelos is determined by three collinear points A, B, and C, and is the curvilinear triangular region between the three semicircles that have AB, BC, and AC as their diameters. If the arbelos is partitioned into two smaller regions by a line segment through the middle point of A, B, and C, perpendicular to line ABC, then each of the two twin circles lies within one of these two regions, tangent to its two semicircular sides and to the splitting segment.

In geometry, the Schoch line is a line defined from an arbelos and named by Peter Woo after Thomas Schoch, who had studied it in conjunction with the Schoch circles.

In geometry, Archimedes' quadruplets are four congruent circles associated with an arbelos. Introduced by Frank Power in the summer of 1998, each have the same area as Archimedes' twin circles, making them Archimedean circles.

The Book of Lemmas is a book attributed to Archimedes by Thābit ibn Qurra, though the authorship of the book is questionable. It consists of fifteen propositions (lemmas) on circles.
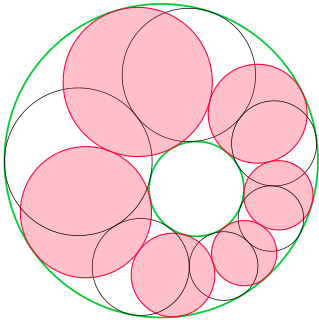
In geometry, a Steiner chain is a set of n circles, all of which are tangent to two given non-intersecting circles, where n is finite and each circle in the chain is tangent to the previous and next circles in the chain. In the usual closed Steiner chains, the first and last (nth) circles are also tangent to each other; by contrast, in open Steiner chains, they need not be. The given circles α and β do not intersect, but otherwise are unconstrained; the smaller circle may lie completely inside or outside of the larger circle. In these cases, the centers of Steiner-chain circles lie on an ellipse or a hyperbola, respectively.
In geometry, the Schoch circles are twelve Archimedean circles constructed by Thomas Schoch.
In geometry, tangent circles are circles in a common plane that intersect in a single point. There are two types of tangency: internal and external. Many problems and constructions in geometry are related to tangent circles; such problems often have real-life applications such as trilateration and maximizing the use of materials.
In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.

















