Related Research Articles

In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's Last Theorem, have shaped much of mathematical history as new areas of mathematics are developed in order to prove them.

The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as
The de Bruijn–Newman constant, denoted by Λ and named after Nicolaas Govert de Bruijn and Charles Michael Newman, is a mathematical constant defined via the zeros of a certain function H(λ,z), where λ is a real parameter and z is a complex variable. More precisely,

In number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, states that
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function. One can then ask the same question about the zeros of these L-functions, yielding various generalizations of the Riemann hypothesis. Many mathematicians believe these generalizations of the Riemann hypothesis to be true. The only cases of these conjectures which have been proven occur in the algebraic function field case.
In mathematics, the Weil conjectures were highly influential proposals by André Weil (1949). They led to a successful multi-decade program to prove them, in which many leading researchers developed the framework of modern algebraic geometry and number theory.
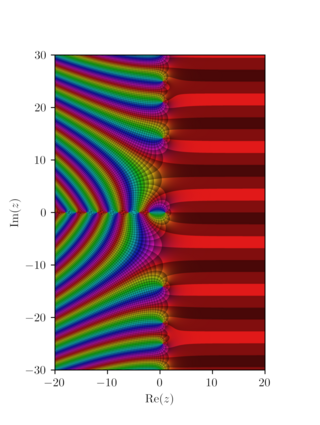
In mathematics, an L-function is a meromorphic function on the complex plane, associated to one out of several categories of mathematical objects. An L-series is a Dirichlet series, usually convergent on a half-plane, that may give rise to an L-function via analytic continuation. The Riemann zeta function is an example of an L-function, and one important conjecture involving L-functions is the Riemann hypothesis and its generalization.
In number theory, Skewes's number is any of several large numbers used by the South African mathematician Stanley Skewes as upper bounds for the smallest natural number for which

In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions. It is well known for its results on prime numbers and additive number theory.

In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by π(x) (unrelated to the number π).
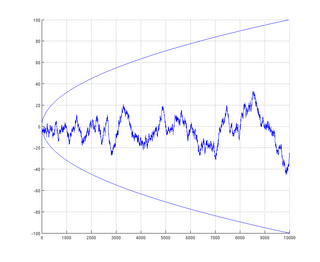
In mathematics, the Mertens conjecture is the statement that the Mertens function is bounded by . Although now disproven, it had been shown to imply the Riemann hypothesis. It was conjectured by Thomas Joannes Stieltjes, in an 1885 letter to Charles Hermite, and again in print by Franz Mertens (1897), and disproved by Andrew Odlyzko and Herman te Riele (1985). It is a striking example of a mathematical conjecture proven false despite a large amount of computational evidence in its favor.

In number theory, the Mertens function is defined for all positive integers n as
In mathematics, the Hilbert–Pólya conjecture states that the non-trivial zeros of the Riemann zeta function correspond to eigenvalues of a self-adjoint operator. It is a possible approach to the Riemann hypothesis, by means of spectral theory.
In mathematics, the Lindelöf hypothesis is a conjecture by Finnish mathematician Ernst Leonard Lindelöf about the rate of growth of the Riemann zeta function on the critical line. This hypothesis is implied by the Riemann hypothesis. It says that for any ε > 0,
Mathematical challenges generally refer to more basic mathematics such as that experienced in elementary or junior high school, but can extend to any realm of the study. It is commonly accepted that mathematics is a difficult area of study. Even so, it is generally agreed that the difficulty experienced when one attempts to master a topic leads to meaningful, long lasting, rewards. There is a long list of mathematics competitions throughout the world.
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French–English pun, Fun. The name "field with one element" and the notation F1 are only suggestive, as there is no field with one element in classical abstract algebra. Instead, F1 refers to the idea that there should be a way to replace sets and operations, the traditional building blocks for abstract algebra, with other, more flexible objects. Many theories of F1 have been proposed, but it is not clear which, if any, of them give F1 all the desired properties. While there is still no field with a single element in these theories, there is a field-like object whose characteristic is one.
In mathematics, the Odlyzko–Schönhage algorithm is a fast algorithm for evaluating the Riemann zeta function at many points, introduced by (Odlyzko & Schönhage 1988). The main point is the use of the fast Fourier transform to speed up the evaluation of a finite Dirichlet series of length N at O(N) equally spaced values from O(N2) to O(N1+ε) steps (at the cost of storing O(N1+ε) intermediate values). The Riemann–Siegel formula used for calculating the Riemann zeta function with imaginary part T uses a finite Dirichlet series with about N = T1/2 terms, so when finding about N values of the Riemann zeta function it is sped up by a factor of about T1/2. This reduces the time to find the zeros of the zeta function with imaginary part at most T from about T3/2+ε steps to about T1+ε steps.

In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann (1859), after whom it is named.

In mathematics, Montgomery's pair correlation conjecture is a conjecture made by Hugh Montgomery (1973) that the pair correlation between pairs of zeros of the Riemann zeta function is
In the study of the Riemann hypothesis, a Lehmer pair is a pair of zeros of the Riemann zeta function that are unusually close to each other. They are named after Derrick Henry Lehmer, who discovered the pair of zeros
References
- ↑ Zeta Finished – Free-DC Forum
- ↑ Ed Pegg Jr. «Ten Trillion Zeta Zeros»
- ↑ "ZetaGrid - News". 2010-11-18. Archived from the original on 2010-11-18. Retrieved 2023-06-04.
- ↑ Yannick Saouter, Xavier Gourdon and Patrick Demichel. An improved lower bound for the de Bruijn-Newman constant. Math. Comp. 80 (2011) 2283. MR 2813360.
- ↑ Yannick Saouter and Patrick Demichel. A sharp region where π(x)−li(x) is positive. Math. Comp. 79 (2010) 2398. MR 2684372.