Related Research Articles
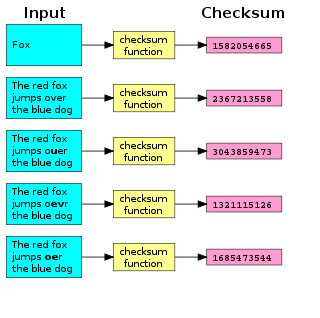
A checksum is a small-sized block of data derived from another block of digital data for the purpose of detecting errors that may have been introduced during its transmission or storage. By themselves, checksums are often used to verify data integrity but are not relied upon to verify data authenticity.

In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
Information theory is the mathematical study of the quantification, storage, and communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. The field, in applied mathematics, is at the intersection of probability theory, statistics, computer science, statistical mechanics, information engineering, and electrical engineering.
UTF-8 is a variable-length character encoding standard used for electronic communication. Defined by the Unicode Standard, the name is derived from Unicode Transformation Format – 8-bit.
A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to digital data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents. On retrieval, the calculation is repeated and, in the event the check values do not match, corrective action can be taken against data corruption. CRCs can be used for error correction.
In digital transmission, the number of bit errors is the numbers of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.
In telecommunication, a convolutional code is a type of error-correcting code that generates parity symbols via the sliding application of a boolean polynomial function to a data stream. The sliding application represents the 'convolution' of the encoder over the data, which gives rise to the term 'convolutional coding'. The sliding nature of the convolutional codes facilitates trellis decoding using a time-invariant trellis. Time invariant trellis decoding allows convolutional codes to be maximum-likelihood soft-decision decoded with reasonable complexity.
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three. Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.
Reed–Solomon codes are a group of error-correcting codes that were introduced by Irving S. Reed and Gustave Solomon in 1960. They have many applications, the most prominent of which include consumer technologies such as MiniDiscs, CDs, DVDs, Blu-ray discs, QR codes, data transmission technologies such as DSL and WiMAX, broadcast systems such as satellite communications, DVB and ATSC, and storage systems such as RAID 6.
A prefix code is a type of code system distinguished by its possession of the "prefix property", which requires that there is no whole code word in the system that is a prefix of any other code word in the system. It is trivially true for fixed-length code, so only a point of consideration in variable-length code.

Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data.
In information theory, turbo codes are a class of high-performance forward error correction (FEC) codes developed around 1990–91, but first published in 1993. They were the first practical codes to closely approach the maximum channel capacity or Shannon limit, a theoretical maximum for the code rate at which reliable communication is still possible given a specific noise level. Turbo codes are used in 3G/4G mobile communications and in satellite communications as well as other applications where designers seek to achieve reliable information transfer over bandwidth- or latency-constrained communication links in the presence of data-corrupting noise. Turbo codes compete with low-density parity-check (LDPC) codes, which provide similar performance.
In information theory, a low-density parity-check (LDPC) code is a linear error correcting code, a method of transmitting a message over a noisy transmission channel. An LDPC code is constructed using a sparse Tanner graph. LDPC codes are capacity-approaching codes, which means that practical constructions exist that allow the noise threshold to be set very close to the theoretical maximum for a symmetric memoryless channel. The noise threshold defines an upper bound for the channel noise, up to which the probability of lost information can be made as small as desired. Using iterative belief propagation techniques, LDPC codes can be decoded in time linear in their block length.
A Viterbi decoder uses the Viterbi algorithm for decoding a bitstream that has been encoded using a convolutional code or trellis code.
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.

The Hadamard code is an error-correcting code named after Jacques Hadamard that is used for error detection and correction when transmitting messages over very noisy or unreliable channels. In 1971, the code was used to transmit photos of Mars back to Earth from the NASA space probe Mariner 9. Because of its unique mathematical properties, the Hadamard code is not only used by engineers, but also intensely studied in coding theory, mathematics, and theoretical computer science. The Hadamard code is also known under the names Walsh code, Walsh family, and Walsh–Hadamard code in recognition of the American mathematician Joseph Leonard Walsh.
In coding theory, concatenated codes form a class of error-correcting codes that are derived by combining an inner code and an outer code. They were conceived in 1966 by Dave Forney as a solution to the problem of finding a code that has both exponentially decreasing error probability with increasing block length and polynomial-time decoding complexity. Concatenated codes became widely used in space communications in the 1970s.
A locally decodable code (LDC) is an error-correcting code that allows a single bit of the original message to be decoded with high probability by only examining a small number of bits of a possibly corrupted codeword. This property could be useful, say, in a context where information is being transmitted over a noisy channel, and only a small subset of the data is required at a particular time and there is no need to decode the entire message at once. Note that locally decodable codes are not a subset of locally testable codes, though there is some overlap between the two.
In information theory, the computationally bounded adversary problem is a different way of looking at the problem of sending data over a noisy channel. In previous models the best that could be done was ensuring correct decoding for up to d/2 errors, where d was the Hamming distance of the code. The problem with doing it this way is that it does not take into consideration the actual amount of computing power available to the adversary. Rather, it only concerns itself with how many bits of a given code word can change and still have the message decode properly. In the computationally bounded adversary model the channel – the adversary – is restricted to only being able to perform a reasonable amount of computation to decide which bits of the code word need to change. In other words, this model does not need to consider how many errors can possibly be handled, but only how many errors could possibly be introduced given a reasonable amount of computing power on the part of the adversary. Once the channel has been given this restriction it becomes possible to construct codes that are both faster to encode and decode compared to previous methods that can also handle a large number of errors.
Sudoku codes are non-linear forward error correcting codes following rules of sudoku puzzles designed for an erasure channel. Based on this model, the transmitter sends a sequence of all symbols of a solved sudoku. The receiver either receives a symbol correctly or an erasure symbol to indicate that the symbol was not received. The decoder gets a matrix with missing entries and uses the constraints of sudoku puzzles to reconstruct a limited amount of erased symbols.
References
- ↑ Ping, Li; Huang, Xiaoling; Phamdo, Nam (2001), "Zigzag codes and concatenated zigzag codes", IEEE Transactions on Information Theory , 47 (2): 800–807, CiteSeerX 10.1.1.107.2616 , doi:10.1109/18.910590, MR 1820492 .