
In mathematics, an associative algebraA is an algebraic structure with compatible operations of addition, multiplication, and a scalar multiplication by elements in some field K. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over the field K. A standard first example of a K-algebra is a ring of square matrices over a field K, with the usual matrix multiplication.
In mathematics, the tensor product of two vector spaces V and W is a vector space to which is associated a bilinear map that maps a pair to an element of denoted
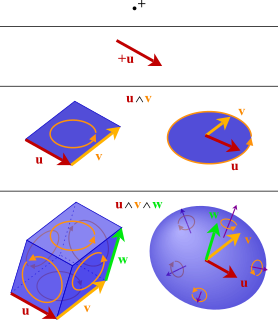
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogues. The exterior product of two vectors and , denoted by , is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of can be interpreted as the area of the parallelogram with sides and , which in three dimensions can also be computed using the cross product of the two vectors. More generally, all parallel plane surfaces with the same orientation and area have the same bivector as a measure of their oriented area. Like the cross product, the exterior product is anticommutative, meaning that for all vectors and , but, unlike the cross product, the exterior product is associative.
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2‑grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry. In most of these theories, the even elements of the superalgebra correspond to bosons and odd elements to fermions.

In mathematics and theoretical physics, the term quantum group denotes one of a few different kinds of noncommutative algebras with additional structure. These include Drinfeld–Jimbo type quantum groups, compact matrix quantum groups, and bicrossproduct quantum groups. Despite their name, they do not themselves have a natural group structure, though they are in some sense 'close' to a group.
In mathematics, the tensor algebra of a vector space V, denoted T(V) or T•(V), is the algebra of tensors on V with multiplication being the tensor product. It is the free algebra on V, in the sense of being left adjoint to the forgetful functor from algebras to vector spaces: it is the "most general" algebra containing V, in the sense of the corresponding universal property.
In mathematics, the Koszul complex was first introduced to define a cohomology theory for Lie algebras, by Jean-Louis Koszul. It turned out to be a useful general construction in homological algebra. As a tool, its homology can be used to tell when a set of elements of a (local) ring is an M-regular sequence, and hence it can be used to prove basic facts about the depth of a module or ideal which is an algebraic notion of dimension that is related to but different from the geometric notion of Krull dimension. Moreover, in certain circumstances, the complex is the complex of syzygies, that is, it tells you the relations between generators of a module, the relations between these relations, and so forth.
In mathematics, the Kronecker product, sometimes denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It is a generalization of the outer product from vectors to matrices, and gives the matrix of the tensor product linear map with respect to a standard choice of basis. The Kronecker product is to be distinguished from the usual matrix multiplication, which is an entirely different operation. The Kronecker product is also sometimes called matrix direct product.
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite-dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in the 1930s by Richard Brauer and Cecil Nesbitt and were named after Georg Frobenius. Tadashi Nakayama discovered the beginnings of a rich duality theory, . Jean Dieudonné used this to characterize Frobenius algebras. Frobenius algebras were generalized to quasi-Frobenius rings, those Noetherian rings whose right regular representation is injective. In recent times, interest has been renewed in Frobenius algebras due to connections to topological quantum field theory.
In mathematics, in particular abstract algebra and topology, a differential graded algebra is a graded associative algebra with an added chain complex structure that respects the algebra structure.
In mathematics, an operad is a structure that consists of abstract operations, each one having a fixed finite number of inputs (arguments) and one output, as well as a specification of how to compose these operations. Given an operad , one defines an algebra over to be a set together with concrete operations on this set which behave just like the abstract operations of . For instance, there is a Lie operad such that the algebras over are precisely the Lie algebras; in a sense abstractly encodes the operations that are common to all Lie algebras. An operad is to its algebras as a group is to its group representations.
In mathematics, a (right) Leibniz algebra, named after Gottfried Wilhelm Leibniz, sometimes called a Loday algebra, after Jean-Louis Loday, is a module L over a commutative ring R with a bilinear product [ _, _ ] satisfying the Leibniz identity
In abstract algebra, a Koszul algebra is a graded -algebra over which the ground field has a linear minimal graded free resolution, i.e., there exists an exact sequence:
In mathematics, Hochschild homology is a homology theory for associative algebras over rings. There is also a theory for Hochschild homology of certain functors. Hochschild cohomology was introduced by Gerhard Hochschild (1945) for algebras over a field, and extended to algebras over more general rings by Henri Cartan and Samuel Eilenberg (1956).
In mathematics, the Butcher group, named after the New Zealand mathematician John C. Butcher by Hairer & Wanner (1974), is an infinite-dimensional Lie group first introduced in numerical analysis to study solutions of non-linear ordinary differential equations by the Runge–Kutta method. It arose from an algebraic formalism involving rooted trees that provides formal power series solutions of the differential equation modeling the flow of a vector field. It was Cayley (1857), prompted by the work of Sylvester on change of variables in differential calculus, who first noted that the derivatives of a composition of functions can be conveniently expressed in terms of rooted trees and their combinatorics.
Geometry of quantum systems is mainly phrased in algebraic terms of modules and algebras. Connections on modules are generalization of a linear connection on a smooth vector bundle written as a Koszul connection on the -module of sections of .
In mathematics, the standard complex, also called standard resolution, bar resolution, bar complex, bar construction, is a way of constructing resolutions in homological algebra. It was first introduced for the special case of algebras over a commutative ring by Samuel Eilenberg and Saunders Mac Lane (1953) and Henri Cartan and Eilenberg (1956, IX.6) and has since been generalized in many ways.
Jean-Louis Loday was a French mathematician who worked on cyclic homology and who introduced Leibniz algebras and Zinbiel algebras. He occasionally used the pseudonym Guillaume William Zinbiel, formed by reversing the last name of Gottfried Wilhelm Leibniz.
In mathematics, Koszul duality, named after the French mathematician Jean-Louis Koszul, is any of various kinds of dualities found in representation theory of Lie algebras, abstract algebras and topology. The prototype example, due to Joseph Bernstein, Israel Gelfand, and Sergei Gelfand, is the rough duality between the derived category of a symmetric algebra and that of an exterior algebra. The importance of the notion rests on the suspicion that Koszul duality seems quite ubiquitous in nature.
In mathematics, an algebra such as has multiplication whose associativity is well-defined on the nose. This means for any real numbers we have






