Astronomical coordinate systems

Last updated May 14, 2024

In astronomy, coordinate systems are used for specifying positions of celestial objects (satellites, planets, stars, galaxies, etc.) relative to a given reference frame, based on physical reference points available to a situated observer (e.g. the true horizon and north to an observer on Earth's surface).^[1] Coordinate systems in astronomy can specify an object's position in three-dimensional space or plot merely its direction on a celestial sphere, if the object's distance is unknown or trivial.

Spherical coordinates, projected on the celestial sphere, are analogous to the geographic coordinate system used on the surface of Earth. These differ in their choice of fundamental plane, which divides the celestial sphere into two equal hemispheres along a great circle. Rectangular coordinates, in appropriate units, have the same fundamental ( $x, y$ ) plane and primary ( $x$ -axis) direction, such as an axis of rotation. Each coordinate system is named after its choice of fundamental plane.

Coordinate systems

The following table lists the common coordinate systems in use by the astronomical community. The fundamental plane divides the celestial sphere into two equal hemispheres and defines the baseline for the latitudinal coordinates, similar to the equator in the geographic coordinate system. The poles are located at ±90° from the fundamental plane. The primary direction is the starting point of the longitudinal coordinates. The origin is the zero distance point, the "center of the celestial sphere", although the definition of celestial sphere is ambiguous about the definition of its center point.

Coordinate system^[2]	Center point (origin)	Fundamental plane (0° latitude)	Poles	Coordinates		Primary direction (0° longitude)
Coordinate system^[2]	Center point (origin)	Fundamental plane (0° latitude)	Poles	Latitude	Longitude	Primary direction (0° longitude)
Horizontal (also called alt-az or el-az)	Observer	Horizon	Zenith, nadir	Altitude ( $a$ ) or elevation	Azimuth ( $A$ )	North or south point of horizon
Equatorial	Center of the Earth (geocentric), or Sun (heliocentric)	Celestial equator	Celestial poles	Declination ( $δ$ )	Right ascension ( $α$ ) or hour angle ( $h$ )	March equinox
Ecliptic	Center of the Earth (geocentric), or Sun (heliocentric)	Ecliptic	Ecliptic poles	Ecliptic latitude ( $β$ )	Ecliptic longitude ( $λ$ )	March equinox
Galactic	Center of the Sun	Galactic plane	Galactic poles	Galactic latitude ( $b$ )	Galactic longitude ( $l$ )	Galactic Center
Supergalactic		Supergalactic plane	Supergalactic poles	Supergalactic latitude ( $SGB$ )	Supergalactic longitude ( $SGL$ )	Intersection of supergalactic plane and galactic plane

Horizontal system

The horizontal, or altitude-azimuth, system is based on the position of the observer on Earth, which revolves around its own axis once per sidereal day (23 hours, 56 minutes and 4.091 seconds) in relation to the star background. The positioning of a celestial object by the horizontal system varies with time, but is a useful coordinate system for locating and tracking objects for observers on Earth. It is based on the position of stars relative to an observer's ideal horizon.

Equatorial system

The equatorial coordinate system is centered at Earth's center, but fixed relative to the celestial poles and the March equinox. The coordinates are based on the location of stars relative to Earth's equator if it were projected out to an infinite distance. The equatorial describes the sky as seen from the Solar System, and modern star maps almost exclusively use equatorial coordinates.

The equatorial system is the normal coordinate system for most professional and many amateur astronomers having an equatorial mount that follows the movement of the sky during the night. Celestial objects are found by adjusting the telescope's or other instrument's scales so that they match the equatorial coordinates of the selected object to observe.

Popular choices of pole and equator are the older B1950 and the modern J2000 systems, but a pole and equator "of date" can also be used, meaning one appropriate to the date under consideration, such as when a measurement of the position of a planet or spacecraft is made. There are also subdivisions into "mean of date" coordinates, which average out or ignore nutation, and "true of date," which include nutation.

Ecliptic system

The fundamental plane is the plane of the Earth's orbit, called the ecliptic plane. There are two principal variants of the ecliptic coordinate system: geocentric ecliptic coordinates centered on the Earth and heliocentric ecliptic coordinates centered on the center of mass of the Solar System.

The geocentric ecliptic system was the principal coordinate system for ancient astronomy and is still useful for computing the apparent motions of the Sun, Moon, and planets.^[3] It was used to define the twelve astrological signs of the zodiac, for instance.

The heliocentric ecliptic system describes the planets' orbital movement around the Sun, and centers on the barycenter of the Solar System (i.e. very close to the center of the Sun). The system is primarily used for computing the positions of planets and other Solar System bodies, as well as defining their orbital elements.

Galactic system

The galactic coordinate system uses the approximate plane of the Milky Way Galaxy as its fundamental plane. The Solar System is still the center of the coordinate system, and the zero point is defined as the direction towards the Galactic Center. Galactic latitude resembles the elevation above the galactic plane and galactic longitude determines direction relative to the center of the galaxy.

Supergalactic system

The supergalactic coordinate system corresponds to a fundamental plane that contains a higher than average number of local galaxies in the sky as seen from Earth.

Converting coordinates

Conversions between the various coordinate systems are given.^[4] See the notes before using these equations.

Notation

Horizontal coordinates
- $A$ , azimuth
- $a$ , altitude
Equatorial coordinates
- $α$ , right ascension
- $δ$ , declination
- $h$ , hour angle
Ecliptic coordinates
- $λ$ , ecliptic longitude
- $β$ , ecliptic latitude
Galactic coordinates
- $l$ , galactic longitude
- $b$ , galactic latitude
Miscellaneous
- $λ o$ , observer's longitude
- $ϕ o$ , observer's latitude
- $ε$ , obliquity of the ecliptic (about 23.4°)
- $θ L$ , local sidereal time
- $θ G$ , Greenwich sidereal time

Hour angle ↔ right ascension

{\begin{aligned}h&=\theta _{\text{L}}-\alpha &&{\mbox{or}}&h&=\theta _{\text{G}}+\lambda _{\text{o}}-\alpha \\\alpha &=\theta _{\text{L}}-h&&{\mbox{or}}&\alpha &=\theta _{\text{G}}+\lambda _{\text{o}}-h\end{aligned}}

Equatorial ↔ ecliptic

The classical equations, derived from spherical trigonometry, for the longitudinal coordinate are presented to the right of a bracket; dividing the first equation by the second gives the convenient tangent equation seen on the left.^[5] The rotation matrix equivalent is given beneath each case.^[6] This division is ambiguous because tan has a period of 180° ( $π$ ) whereas cos and sin have periods of 360° (2 $π$ ).

{\begin{aligned}\tan \left(\lambda \right)&={\sin \left(\alpha \right)\cos \left(\varepsilon \right)+\tan \left(\delta \right)\sin \left(\varepsilon \right) \over \cos \left(\alpha \right)};\qquad {\begin{cases}\cos \left(\beta \right)\sin \left(\lambda \right)=\cos \left(\delta \right)\sin \left(\alpha \right)\cos \left(\varepsilon \right)+\sin \left(\delta \right)\sin \left(\varepsilon \right);\\\cos \left(\beta \right)\cos \left(\lambda \right)=\cos \left(\delta \right)\cos \left(\alpha \right).\end{cases}}\\\sin \left(\beta \right)&=\sin \left(\delta \right)\cos \left(\varepsilon \right)-\cos \left(\delta \right)\sin \left(\varepsilon \right)\sin \left(\alpha \right)\\[3pt]{\begin{bmatrix}\cos \left(\beta \right)\cos \left(\lambda \right)\\\cos \left(\beta \right)\sin \left(\lambda \right)\\\sin \left(\beta \right)\end{bmatrix}}&={\begin{bmatrix}1&0&0\\0&\cos \left(\varepsilon \right)&\sin \left(\varepsilon \right)\\0&-\sin \left(\varepsilon \right)&\cos \left(\varepsilon \right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}}\\[6pt]\tan \left(\alpha \right)&={\sin \left(\lambda \right)\cos \left(\varepsilon \right)-\tan \left(\beta \right)\sin \left(\varepsilon \right) \over \cos \left(\lambda \right)};\qquad {\begin{cases}\cos \left(\delta \right)\sin \left(\alpha \right)=\cos \left(\beta \right)\sin \left(\lambda \right)\cos \left(\varepsilon \right)-\sin \left(\beta \right)\sin \left(\varepsilon \right);\\\cos \left(\delta \right)\cos \left(\alpha \right)=\cos \left(\beta \right)\cos \left(\lambda \right).\end{cases}}\\[3pt]\sin \left(\delta \right)&=\sin \left(\beta \right)\cos \left(\varepsilon \right)+\cos \left(\beta \right)\sin \left(\varepsilon \right)\sin \left(\lambda \right).\\[6pt]{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}}&={\begin{bmatrix}1&0&0\\0&\cos \left(\varepsilon \right)&-\sin \left(\varepsilon \right)\\0&\sin \left(\varepsilon \right)&\cos \left(\varepsilon \right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\beta \right)\cos \left(\lambda \right)\\\cos \left(\beta \right)\sin \left(\lambda \right)\\\sin \left(\beta \right)\end{bmatrix}}.\end{aligned}}

Equatorial ↔ horizontal

Azimuth ( $A$ ) is measured from the south point, turning positive to the west.^[7] Zenith distance, the angular distance along the great circle from the zenith to a celestial object, is simply the complementary angle of the altitude: $90° - a$ .^[8]

{\begin{aligned}\tan \left(A\right)&={\sin \left(h\right) \over \cos \left(h\right)\sin \left(\phi _{\text{o}}\right)-\tan \left(\delta \right)\cos \left(\phi _{\text{o}}\right)};\qquad {\begin{cases}\cos \left(a\right)\sin \left(A\right)=\cos \left(\delta \right)\sin \left(h\right);\\\cos \left(a\right)\cos \left(A\right)=\cos \left(\delta \right)\cos \left(h\right)\sin \left(\phi _{\text{o}}\right)-\sin \left(\delta \right)\cos \left(\phi _{\text{o}}\right)\end{cases}}\\[3pt]\sin \left(a\right)&=\sin \left(\phi _{\text{o}}\right)\sin \left(\delta \right)+\cos \left(\phi _{\text{o}}\right)\cos \left(\delta \right)\cos \left(h\right);\end{aligned}}

In solving the $tan(A)$ equation for $A$ , in order to avoid the ambiguity of the arctangent, use of the two-argument arctangent, denoted $arctan(x, y)$ , is recommended. The two-argument arctangent computes the arctangent of $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}y/x$ , and accounts for the quadrant in which it is being computed. Thus, consistent with the convention of azimuth being measured from the south and opening positive to the west,

A=-\arctan(x,y)

,

where

{\begin{aligned}x&=-\sin \left(\phi _{\text{o}}\right)\cos \left(\delta \right)\cos \left(h\right)+\cos \left(\phi _{\text{o}}\right)\sin \left(\delta \right)\\y&=\cos \left(\delta \right)\sin \left(h\right)\end{aligned}}

.

If the above formula produces a negative value for $A$ , it can be rendered positive by simply adding 360°.

{\begin{aligned}{\begin{bmatrix}\cos \left(a\right)\cos \left(A\right)\\\cos \left(a\right)\sin \left(A\right)\\\sin \left(a\right)\end{bmatrix}}&={\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&-\cos \left(\phi _{\text{o}}\right)\\0&1&0\\\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\delta \right)\cos \left(h\right)\\\cos \left(\delta \right)\sin \left(h\right)\\\sin \left(\delta \right)\end{bmatrix}}\\&={\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&-\cos \left(\phi _{\text{o}}\right)\\0&1&0\\\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\theta _{L}\right)&\sin \left(\theta _{L}\right)&0\\\sin \left(\theta _{L}\right)&-\cos \left(\theta _{L}\right)&0\\0&0&1\end{bmatrix}}{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}};\\[6pt]\tan \left(h\right)&={\sin \left(A\right) \over \cos \left(A\right)\sin \left(\phi _{\text{o}}\right)+\tan \left(a\right)\cos \left(\phi _{\text{o}}\right)};\qquad {\begin{cases}\cos \left(\delta \right)\sin \left(h\right)=\cos \left(a\right)\sin \left(A\right);\\\cos \left(\delta \right)\cos \left(h\right)=\sin \left(a\right)\cos \left(\phi _{\text{o}}\right)+\cos \left(a\right)\cos \left(A\right)\sin \left(\phi _{\text{o}}\right)\end{cases}}\\[3pt]\sin \left(\delta \right)&=\sin \left(\phi _{\text{o}}\right)\sin \left(a\right)-\cos \left(\phi _{\text{o}}\right)\cos \left(a\right)\cos \left(A\right);\end{aligned}}

^{[lower-alpha 1]}

Again, in solving the $tan(h)$ equation for $h$ , use of the two-argument arctangent that accounts for the quadrant is recommended. Thus, again consistent with the convention of azimuth being measured from the south and opening positive to the west,

h=\arctan(x,y)

,

where

{\begin{aligned}x&=\sin \left(\phi _{\text{o}}\right)\cos \left(a\right)\cos \left(A\right)+\cos \left(\phi _{\text{o}}\right)\sin \left(a\right)\\y&=\cos \left(a\right)\sin \left(A\right)\\[3pt]{\begin{bmatrix}\cos \left(\delta \right)\cos \left(h\right)\\\cos \left(\delta \right)\sin \left(h\right)\\\sin \left(\delta \right)\end{bmatrix}}&={\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&\cos \left(\phi _{\text{o}}\right)\\0&1&0\\-\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(a\right)\cos \left(A\right)\\\cos \left(a\right)\sin \left(A\right)\\\sin \left(a\right)\end{bmatrix}}\\{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}}&={\begin{bmatrix}\cos \left(\theta _{L}\right)&\sin \left(\theta _{L}\right)&0\\\sin \left(\theta _{L}\right)&-\cos \left(\theta _{L}\right)&0\\0&0&1\end{bmatrix}}{\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&\cos \left(\phi _{\text{o}}\right)\\0&1&0\\-\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(a\right)\cos \left(A\right)\\\cos \left(a\right)\sin \left(A\right)\\\sin \left(a\right)\end{bmatrix}}.\end{aligned}}

Equatorial ↔ galactic

These equations^[14] are for converting equatorial coordinates to Galactic coordinates.

{\begin{aligned}\cos \left(l_{\text{NCP}}-l\right)\cos(b)&=\sin \left(\delta \right)\cos \left(\delta _{\text{G}}\right)-\cos \left(\delta \right)\sin \left(\delta _{\text{G}}\right)\cos \left(\alpha -\alpha _{\text{G}}\right)\\\sin \left(l_{\text{NCP}}-l\right)\cos(b)&=\cos(\delta )\sin \left(\alpha -\alpha _{\text{G}}\right)\\\sin \left(b\right)&=\sin \left(\delta \right)\sin \left(\delta _{\text{G}}\right)+\cos \left(\delta \right)\cos \left(\delta _{\text{G}}\right)\cos \left(\alpha -\alpha _{\text{G}}\right)\end{aligned}}

run_going

$\alpha _{\text{G}},\delta _{\text{G}}$ are the equatorial coordinates of the North Galactic Pole and $l_{\text{NCP}}$ is the Galactic longitude of the North Celestial Pole. Referred to J2000.0 the values of these quantities are:

\alpha _{G}=192.85948^{\circ }\qquad \delta _{G}=27.12825^{\circ }\qquad l_{\text{NCP}}=122.93192^{\circ }

If the equatorial coordinates are referred to another equinox, they must be precessed to their place at J2000.0 before applying these formulae.

These equations convert to equatorial coordinates referred to B2000.0.

{\begin{aligned}\sin \left(\alpha -\alpha _{\text{G}}\right)\cos \left(\delta \right)&=\cos \left(b\right)\sin \left(l_{\text{NCP}}-l\right)\\\cos \left(\alpha -\alpha _{\text{G}}\right)\cos \left(\delta \right)&=\sin \left(b\right)\cos \left(\delta _{\text{G}}\right)-\cos \left(b\right)\sin \left(\delta _{\text{G}}\right)\cos \left(l_{\text{NCP}}-l\right)\\\sin \left(\delta \right)&=\sin \left(b\right)\sin \left(\delta _{\text{G}}\right)+\cos \left(b\right)\cos \left(\delta _{\text{G}}\right)\cos \left(l_{\text{NCP}}-l\right)\end{aligned}}

>laft_spasse>11.3

Notes on conversion

Angles in the degrees ( ° ), minutes ( ′ ), and seconds ( ″ ) of sexagesimal measure must be converted to decimal before calculations are performed. Whether they are converted to decimal degrees or radians depends upon the particular calculating machine or program. Negative angles must be carefully handled; –10° 20′ 30″ must be converted as −10° −20′ −30″.
Angles in the hours ( ^h ), minutes ( ^m ), and seconds ( ^s ) of time measure must be converted to decimal degrees or radians before calculations are performed. 1^h = 15°; 1^m = 15′; 1^s = 15″
Angles greater than 360° (2 $π$ ) or less than 0° may need to be reduced to the range 0°−360° (0–2 $π$ ) depending upon the particular calculating machine or program.
The cosine of a latitude (declination, ecliptic and Galactic latitude, and altitude) are never negative by definition, since the latitude varies between −90° and +90°.
Inverse trigonometric functions arcsine, arccosine and arctangent are quadrant-ambiguous, and results should be carefully evaluated. Use of the second arctangent function (denoted in computing as atn2(y,x) or atan2(y,x), which calculates the arctangent of $y / x$ using the sign of both arguments to determine the right quadrant) is recommended when calculating longitude/right ascension/azimuth. An equation which finds the sine, followed by the arcsin function, is recommended when calculating latitude/declination/altitude.
Azimuth ( $A$ ) is referred here to the south point of the horizon, the common astronomical reckoning. An object on the meridian to the south of the observer has $A$ = $h$ = 0° with this usage. However, n Astropy's AltAz, in the Large Binocular Telescope FITS file convention, in XEphem, in the IAU library Standards of Fundamental Astronomy and Section B of the Astronomical Almanac for example, the azimuth is East of North. In navigation and some other disciplines, azimuth is figured from the north.
The equations for altitude ( $a$ ) do not account for atmospheric refraction.
The equations for horizontal coordinates do not account for diurnal parallax, that is, the small offset in the position of a celestial object caused by the position of the observer on the Earth's surface. This effect is significant for the Moon, less so for the planets, minute for stars or more distant objects.
Observer's longitude ( $λ o$ ) here is measured positively westward from the prime meridian; this is contrary to current IAU standards.

Notes

↑ Depending on the azimuth convention in use, the signs of $cos A$ and $sin A$ appear in all four different combinations. Karttunen et al.,^[9] Taff,^[10] and Roth^[11] define $A$ clockwise from the south. Lang^[12] defines it north through east, Smart^[13] north through west. Meeus (1991),^[4] p. 89: $sin δ = sin φ sin a - cos φ cos a cos A$ ; Explanatory Supplement (1961),^[5] p. 26: $sin δ = sin a sin φ + cos a cos A cos φ$ .

Related Research Articles

In physics, the cross section is a measure of the probability that a specific process will take place in a collision of two particles. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted $σ$ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

In mathematical physics and mathematics, the Pauli matrices are a set of three $2 \times 2$ complex matrices that are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space $under the operation of composition.$

In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols $, (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δ f (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p) .$

Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.

In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.

In geodesy, conversion among different geographic coordinate systems is made necessary by the different geographic coordinate systems in use across the world and over time. Coordinate conversion is composed of a number of different types of conversion: format change of geographic coordinates, conversion of coordinate systems, or transformation to different geodetic datums. Geographic coordinate conversion has applications in cartography, surveying, navigation and geographic information systems.

In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates $(q, p) \to$ that preserves the form of Hamilton's equations. This is sometimes known as form invariance. Although Hamilton's equations are preserved, it need not preserve the explicit form of the Hamiltonian itself. Canonical transformations are useful in their own right, and also form the basis for the Hamilton–Jacobi equations and Liouville's theorem.

In physics, the S-matrix or scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).

In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. Propagators may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called (causal) Green's functions.

In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.

The solar zenith angle is the zenith angle of the sun, i.e., the angle between the sun’s rays and the vertical direction. It is the complement to the solar altitude or solar elevation, which is the altitude angle or elevation angle between the sun’s rays and a horizontal plane. At solar noon, the zenith angle is at a minimum and is equal to latitude minus solar declination angle. This is the basis by which ancient mariners navigated the oceans.

In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.

In calculus, the Leibniz integral rule for differentiation under the integral sign states that for an integral of the form

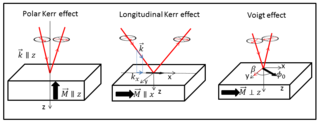
<span class="mw-page-title-main">Voigt effect</span>

The Voigt effect is a magneto-optical phenomenon which rotates and elliptizes linearly polarised light sent into an optically active medium. The effect is named after the German scientist Woldemar Voigt who discovered it in vapors. Unlike many other magneto-optical effects such as the Kerr or Faraday effect which are linearly proportional to the magnetization, the Voigt effect is proportional to the square of the magnetization and can be seen experimentally at normal incidence. There are also other denominations for this effect, used interchangeably in the modern scientific literature: the Cotton–Mouton effect and magnetic-linear birefringence, with the latter reflecting the physical meaning of the effect.

The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members often asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— $in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.$

<span class="mw-page-title-main">Dual quaternion</span> Eight-dimensional algebra over the real numbers

In mathematics, the dual quaternions are an 8-dimensional real algebra isomorphic to the tensor product of the quaternions and the dual numbers. Thus, they may be constructed in the same way as the quaternions, except using dual numbers instead of real numbers as coefficients. A dual quaternion can be represented in the form A + εB, where A and B are ordinary quaternions and ε is the dual unit, which satisfies ε² = 0 and commutes with every element of the algebra. Unlike quaternions, the dual quaternions do not form a division algebra.

The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Since the 8th and 9th centuries, the sine and other trigonometric functions have been used in Islamic mathematics and astronomy, reforming the production of sine tables. Khwarizmi and Habash al-Hasib later produced a set of trigonometric tables.

The Uflyand-Mindlin theory of vibrating plates is an extension of Kirchhoff–Love plate theory that takes into account shear deformations through-the-thickness of a plate. The theory was proposed in 1948 by Yakov Solomonovich Uflyand (1916-1991) and in 1951 by Raymond Mindlin with Mindlin making reference to Uflyand's work. Hence, this theory has to be referred to as Uflyand-Mindlin plate theory, as is done in the handbook by Elishakoff, and in papers by Andronov, Elishakoff, Hache and Challamel, Loktev, Rossikhin and Shitikova and Wojnar. In 1994, Elishakoff suggested to neglect the fourth-order time derivative in Uflyand-Mindlin equations. A similar, but not identical, theory in static setting, had been proposed earlier by Eric Reissner in 1945. Both theories are intended for thick plates in which the normal to the mid-surface remains straight but not necessarily perpendicular to the mid-surface. The Uflyand-Mindlin theory is used to calculate the deformations and stresses in a plate whose thickness is of the order of one tenth the planar dimensions while the Kirchhoff–Love theory is applicable to thinner plates.

In the Newman–Penrose (NP) formalism of general relativity, independent components of the Ricci tensors of a four-dimensional spacetime are encoded into seven Ricci scalars which consist of three real scalars $, three complex scalars and the NP curvature scalar . Physically, Ricci-NP scalars are related with the energy-momentum distribution of the spacetime due to Einstein's field equation.$

References

↑ Kanas, Nick (2021). "Star and Solar System Maps: A History of Celestial Cartography". Research Notes of the AAS. 5 (4). American Astronomical Society: 69. Bibcode:2021RNAAS...5...69K. doi: 10.3847/2515-5172/abf35c . S2CID 233522547.
↑ Majewski, Steve. "Coordinate Systems". UVa Department of Astronomy. Archived from the original on 12 March 2016. Retrieved 19 March 2011.
↑ Aaboe, Asger. 2001 Episodes from the Early History of Astronomy. New York: Springer-Verlag., pp. 17–19.
1 2 Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. ISBN 0-943396-35-2., chap. 12
1 2 U.S. Naval Observatory, Nautical Almanac Office; H.M. Nautical Almanac Office (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London., sec. 2A
↑ U.S. Naval Observatory, Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. ISBN 0-935702-68-7., section 11.43
↑ Montenbruck, Oliver; Pfleger, Thomas (2000). Astronomy on the Personal Computer. Springer-Verlag Berlin Heidelberg. ISBN 978-3-540-67221-0., pp 35-37
↑ U.S. Naval Observatory, Nautical Almanac Office; U.K. Hydrographic Office, H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. M18. ISBN 978-0160820083.
↑ Karttunen, H.; Kröger, P.; Oja, H.; Poutanen, M.; Donner, H. J. (2006). Fundamental Astronomy (5 ed.). Springer. Bibcode:2003fuas.book.....K. ISBN 978-3-540-34143-7.
↑ Taff, L. G. (1981). Computational spherical astronomy. Wiley. Bibcode:1981csa..book.....T. ISBN 0-471-06257-X.
↑ Roth, G. D. (23 October 1989). Handbuch für Sternenfreunde. Springer. ISBN 3-540-19436-3.
↑ Lang, Kenneth R. (1978). Astrophysical Formulae. Springer. Bibcode:1978afcp.book.....L. ISBN 3-540-09064-9.
↑ Smart, William Marshall (1949). Text-book on spherical astronomy. Cambridge University Press. Bibcode:1965tbsa.book.....S.
↑ Poleski, Radosław (2013). "Transformation of the equatorial proper motion to the Galactic system". arXiv: 1306.2945 [astro-ph.IM].

External links

NOVAS, the United States Naval Observatory's Vector Astrometry Software, an integrated package of subroutines and functions for computing various commonly needed quantities in positional astronomy.
SuperNOVAS a maintained fork of NOVAS C 3.1 with bug fixes, improvements, new features, and online documentation.
SOFA, the IAU's Standards of Fundamental Astronomy, an accessible and authoritative set of algorithms and procedures that implement standard models used in fundamental astronomy.
This article was originally based on Jason Harris' Astroinfo, which is accompanied by KStars, a KDE Desktop Planetarium for Linux/KDE.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[14] Depending on the azimuth convention in use, the signs of $cos A$ and $sin A$ appear in all four different combinations. Karttunen et al.,^[9] Taff,^[10] and Roth^[11] define $A$ clockwise from the south. Lang^[12] defines it north through east, Smart^[13] north through west. Meeus (1991),^[4] p. 89: $sin δ = sin φ sin a - cos φ cos a cos A$ ; Explanatory Supplement (1961),^[5] p. 26: $sin δ = sin a sin φ + cos a cos A cos φ$ .

[1] Kanas, Nick (2021). "Star and Solar System Maps: A History of Celestial Cartography". Research Notes of the AAS. 5 (4). American Astronomical Society: 69. Bibcode:2021RNAAS...5...69K. doi: 10.3847/2515-5172/abf35c . S2CID 233522547.

[2] Majewski, Steve. "Coordinate Systems". UVa Department of Astronomy. Archived from the original on 12 March 2016. Retrieved 19 March 2011.

[3] Aaboe, Asger. 2001 Episodes from the Early History of Astronomy. New York: Springer-Verlag., pp. 17–19.

[Meeus-4] 1 2 Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. ISBN 0-943396-35-2., chap. 12

[ExplSupp-5] 1 2 U.S. Naval Observatory, Nautical Almanac Office; H.M. Nautical Almanac Office (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London., sec. 2A

[6] U.S. Naval Observatory, Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. ISBN 0-935702-68-7., section 11.43

[7] Montenbruck, Oliver; Pfleger, Thomas (2000). Astronomy on the Personal Computer. Springer-Verlag Berlin Heidelberg. ISBN 978-3-540-67221-0., pp 35-37

[8] U.S. Naval Observatory, Nautical Almanac Office; U.K. Hydrographic Office, H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. M18. ISBN 978-0160820083.

[Karttunen-9] Karttunen, H.; Kröger, P.; Oja, H.; Poutanen, M.; Donner, H. J. (2006). Fundamental Astronomy (5 ed.). Springer. Bibcode:2003fuas.book.....K. ISBN 978-3-540-34143-7.

[Taff-10] Taff, L. G. (1981). Computational spherical astronomy. Wiley. Bibcode:1981csa..book.....T. ISBN 0-471-06257-X.

[Roth-11] Roth, G. D. (23 October 1989). Handbuch für Sternenfreunde. Springer. ISBN 3-540-19436-3.

[Lang-12] Lang, Kenneth R. (1978). Astrophysical Formulae. Springer. Bibcode:1978afcp.book.....L. ISBN 3-540-09064-9.

[Smart-13] Smart, William Marshall (1949). Text-book on spherical astronomy. Cambridge University Press. Bibcode:1965tbsa.book.....S.

[15] Poleski, Radosław (2013). "Transformation of the equatorial proper motion to the Galactic system". arXiv: 1306.2945 [astro-ph.IM].

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[lower-alpha 1]

[14]

[9]

[10]

[11]

[12]

[13]