Block graph

Last updated
A block graph Block graph.svg
A block graph

In graph theory, a branch of combinatorial mathematics, a block graph or clique tree [1] is a type of undirected graph in which every biconnected component (block) is a clique.

Contents

Block graphs are sometimes erroneously called Husimi trees (after Kôdi Husimi), [2] but that name more properly refers to cactus graphs, graphs in which every nontrivial biconnected component is a cycle. [3]

Block graphs may be characterized as the intersection graphs of the blocks of arbitrary undirected graphs. [4]

Characterization

Block graphs are exactly the graphs for which, for every four vertices u, v, x, and y, the largest two of the three distances d(u,v) + d(x,y), d(u,x) + d(v,y), and d(u,y) + d(v,x) are always equal. [2] [5]

They also have a forbidden graph characterization as the graphs that do not have the diamond graph or a cycle of four or more vertices as an induced subgraph; that is, they are the diamond-free chordal graphs. [5] They are also the Ptolemaic graphs (chordal distance-hereditary graphs) in which every two nodes at distance two from each other are connected by a unique shortest path, [2] and the chordal graphs in which every two maximal cliques have at most one vertex in common. [2]

A graph G is a block graph if and only if the intersection of every two connected subsets of vertices of G is empty or connected. Therefore, the connected subsets of vertices in a connected block graph form a convex geometry, a property that is not true of any graphs that are not block graphs. [6] Because of this property, in a connected block graph, every set of vertices has a unique minimal connected superset, its closure in the convex geometry. The connected block graphs are exactly the graphs in which there is a unique induced path connecting every pair of vertices. [1]

Block graphs are chordal, distance-hereditary, and geodetic. The distance-hereditary graphs are the graphs in which every two induced paths between the same two vertices have the same length, a weakening of the characterization of block graphs as having at most one induced path between every two vertices. Because both the chordal graphs and the distance-hereditary graphs are subclasses of the perfect graphs, block graphs are perfect.

Every tree, cluster graph, or windmill graph is a block graph.

Every block graph has boxicity at most two. [7]

Block graphs are examples of pseudo-median graphs: for every three vertices, either there exists a unique vertex that belongs to shortest paths between all three vertices, or there exists a unique triangle whose edges lie on these three shortest paths. [7]

The line graphs of trees are exactly the block graphs in which every cut vertex is incident to at most two blocks, or equivalently the claw-free block graphs. Line graphs of trees have been used to find graphs with a given number of edges and vertices in which the largest induced subgraph that is a tree is as small as possible. [8]

The block graphs in which every block has size at most three are a special type of cactus graph, a triangular cactus. The largest triangular cactus in any graph may be found in polynomial time using an algorithm for the matroid parity problem. Since triangular cactus graphs are planar graphs, the largest triangular cactus can be used as an approximation to the largest planar subgraph, an important subproblem in planarization. As an approximation algorithm, this method has approximation ratio 4/9, the best known for the maximum planar subgraph problem. [9]

Block graphs of undirected graphs

If G is any undirected graph, the block graph of G, denoted B(G), is the intersection graph of the blocks of G: B(G) has a vertex for every biconnected component of G, and two vertices of B(G) are adjacent if the corresponding two blocks meet at an articulation vertex. If K1 denotes the graph with one vertex, then B(K1) is defined to be the empty graph. B(G) is necessarily a block graph: it has one biconnected component for each articulation vertex of G, and each biconnected component formed in this way must be a clique. Conversely, every block graph is the graph B(G) for some graph G. [4] If G is a tree, then B(G) coincides with the line graph of G.

The graph B(B(G)) has one vertex for each articulation vertex of G; two vertices are adjacent in B(B(G)) if they belong to the same block in G. [4]

Related Research Articles

Hamiltonian path Path in a graph that visits each vertex exactly once

In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. Determining whether such paths and cycles exist in graphs are NP-complete.

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

Outerplanar graph Non-crossing graph with vertices on outer face

In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

In graph theory, an undirected graph H is called a minor of the graph G if H can be formed from G by deleting edges and vertices and by contracting edges.

Perfect graph Graph with tight clique-coloring relation

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the order of the largest clique of that subgraph. Equivalently stated in symbolic terms an arbitrary graph is perfect if and only if for all we have .

Chordal graph Graph where all long cycles have a chord

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

Cograph Graph formed by complementation and disjoint union

In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.

In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly k are called k-trees, and the graphs with treewidth at most k are called partial k-trees. Many other well-studied graph families also have bounded treewidth.

In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

Intersection graph Graph representing intersections between given sets

In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them.

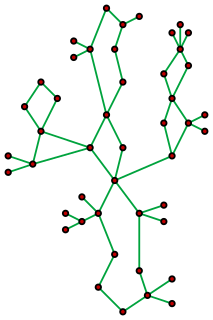
Cactus graph Mathematical tree of cycles

In graph theory, a cactus is a connected graph in which any two simple cycles have at most one vertex in common. Equivalently, it is a connected graph in which every edge belongs to at most one simple cycle, or in which every block is an edge or a cycle.

Peripheral cycle Graph cycle which does not separate remaining elements

In graph theory, a peripheral cycle in an undirected graph is, intuitively, a cycle that does not separate any part of the graph from any other part. Peripheral cycles were first studied by Tutte (1963), and play important roles in the characterization of planar graphs and in generating the cycle spaces of nonplanar graphs.

In graph theory, a clique cover or partition into cliques of a given undirected graph is a partition of the vertices into cliques, subsets of vertices within which every two vertices are adjacent. A minimum clique cover is a clique cover that uses as few cliques as possible. The minimum k for which a clique cover exists is called the clique cover number of the given graph.

Distance-hereditary graph Graph whose induced subgraphs preserve distance

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

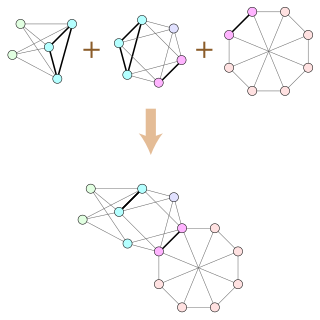
Clique-sum Gluing graphs at complete subgraphs

In graph theory, a branch of mathematics, a clique-sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology. If two graphs G and H each contain cliques of equal size, the clique-sum of G and H is formed from their disjoint union by identifying pairs of vertices in these two cliques to form a single shared clique, and then possibly deleting some of the clique edges. A k-clique-sum is a clique-sum in which both cliques have at most k vertices. One may also form clique-sums and k-clique-sums of more than two graphs, by repeated application of the two-graph clique-sum operation.

In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and Paul Seymour. Its proof is very long and involved. Kawarabayashi & Mohar (2007) and Lovász (2006) are surveys accessible to nonspecialists, describing the theorem and its consequences.

Pancyclic graph

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.

Ptolemaic graph

In graph theory, a Ptolemaic graph is an undirected graph whose shortest path distances obey Ptolemy's inequality, which in turn was named after the Greek astronomer and mathematician Ptolemy. The Ptolemaic graphs are exactly the graphs that are both chordal and distance-hereditary; they include the block graphs and are a subclass of the perfect graphs.

Matroid parity problem Largest independent set of paired elements

In combinatorial optimization, the matroid parity problem is a problem of finding the largest independent set of paired elements in a matroid. The problem was formulated by Lawler (1976) as a common generalization of graph matching and matroid intersection. It is also known as polymatroid matching, or the matchoid problem.

In graph theory, a geodetic graph is an undirected graph such that there exists a unique (unweighted) shortest path between each two vertices.

References

  1. 1 2 Vušković, Kristina (2010), "Even-hole-free graphs: A survey" (PDF), Applicable Analysis and Discrete Mathematics, 4 (2): 219–240, doi:10.2298/AADM100812027V .
  2. 1 2 3 4 Howorka, Edward (1979), "On metric properties of certain clique graphs", Journal of Combinatorial Theory, Series B, 27 (1): 67–74, doi: 10.1016/0095-8956(79)90069-8 .
  3. ↑ See, e.g., MR 0659742, a 1983 review by Robert E. Jamison of another paper referring to block graphs as Husimi trees; Jamison attributes the mistake to an error in a book by Mehdi Behzad and Gary Chartrand.
  4. 1 2 3 Harary, Frank (1963), "A characterization of block-graphs", Canadian Mathematical Bulletin , 6 (1): 1–6, doi: 10.4153/cmb-1963-001-x , hdl: 10338.dmlcz/101399 .
  5. 1 2 Bandelt, Hans-Jürgen; Mulder, Henry Martyn (1986), "Distance-hereditary graphs", Journal of Combinatorial Theory, Series B, 41 (2): 182–208, doi: 10.1016/0095-8956(86)90043-2 .
  6. ↑ Edelman, Paul H.; Jamison, Robert E. (1985), "The theory of convex geometries", Geometriae Dedicata , 19 (3): 247–270, doi: 10.1007/BF00149365 , S2CID   123491343 .
  7. 1 2 Block graphs, Information System on Graph Class Inclusions.
  8. ↑ Erdős, Paul; Saks, Michael; Sós, Vera T. (1986), "Maximum induced trees in graphs" (PDF), Journal of Combinatorial Theory, Series B, 41 (1): 61–79, doi: 10.1016/0095-8956(86)90028-6 .
  9. ↑ Călinescu, Gruia; Fernandes, Cristina G.; Finkler, Ulrich; Karloff, Howard (2002), "A Better Approximation Algorithm for Finding Planar Subgraphs", Journal of Algorithms, 2, 27 (2): 269–302, doi:10.1006/jagm.1997.0920, S2CID   8329680
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.