Branch-decomposition

Last updated November 08, 2023

In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.

Branchwidth is closely related to tree-width: for all graphs, both of these numbers are within a constant factor of each other, and both quantities may be characterized by forbidden minors. And as with treewidth, many graph optimization problems may be solved efficiently for graphs of small branchwidth. However, unlike treewidth, the branchwidth of planar graphs may be computed exactly, in polynomial time. Branch-decompositions and branchwidth may also be generalized from graphs to matroids.

Definitions

An unrooted binary tree is a connected undirected graph with no cycles in which each non-leaf node has exactly three neighbors. A branch-decomposition may be represented by an unrooted binary tree T, together with a bijection between the leaves of T and the edges of the given graph G = (V,E). If e is any edge of the tree T, then removing e from T partitions it into two subtrees T₁ and T₂. This partition of T into subtrees induces a partition of the edges associated with the leaves of T into two subgraphs G₁ and G₂ of G. This partition of G into two subgraphs is called an e-separation.

The width of an e-separation is the number of vertices of G that are incident both to an edge of E₁ and to an edge of E₂; that is, it is the number of vertices that are shared by the two subgraphs G₁ and G₂. The width of the branch-decomposition is the maximum width of any of its e-separations. The branchwidth of G is the minimum width of a branch-decomposition of G.

Relation to treewidth

Branch-decompositions of graphs are closely related to tree decompositions, and branch-width is closely related to tree-width: the two quantities are always within a constant factor of each other. In particular, in the paper in which they introduced branch-width, Neil Robertson and Paul Seymour ^[1] showed that for a graph G with tree-width k and branchwidth b > 1,

b-1\leq k\leq \left\lfloor {\frac {3}{2}}b\right\rfloor -1.

Carving width

Carving width is a concept defined similarly to branch width, except with edges replaced by vertices and vice versa. A carving decomposition is an unrooted binary tree with each leaf representing a vertex in the original graph, and the width of a cut is the number (or total weight in a weighted graph) of edges that are incident to a vertex in both subtrees.

Branch width algorithms typically work by reducing to an equivalent carving width problem. In particular, the carving width of the medial graph of a planar graph is exactly twice the branch width of the original graph.^[2]

Algorithms and complexity

It is NP-complete to determine whether a graph G has a branch-decomposition of width at most k, when G and k are both considered as inputs to the problem.^[2] However, the graphs with branchwidth at most k form a minor-closed family of graphs,^[3] from which it follows that computing the branchwidth is fixed-parameter tractable: there is an algorithm for computing optimal branch-decompositions whose running time, on graphs of branchwidth k for any fixed constant k, is linear in the size of the input graph.^[4]

For planar graphs, the branchwidth can be computed exactly in polynomial time. This in contrast to treewidth for which the complexity on planar graphs is a well known open problem.^[5] The original algorithm for planar branchwidth, by Paul Seymour and Robin Thomas, took time O(n²) on graphs with n vertices, and their algorithm for constructing a branch decomposition of this width took time O(n⁴).^[2] This was later sped up to O(n³).^[6]

As with treewidth, branchwidth can be used as the basis of dynamic programming algorithms for many NP-hard optimization problems, using an amount of time that is exponential in the width of the input graph or matroid.^[7] For instance, Cook & Seymour (2003) apply branchwidth-based dynamic programming to a problem of merging multiple partial solutions to the travelling salesman problem into a single global solution, by forming a sparse graph from the union of the partial solutions, using a spectral clustering heuristic to find a good branch-decomposition of this graph, and applying dynamic programming to the decomposition. Fomin & Thilikos (2006) argue that branchwidth works better than treewidth in the development of fixed-parameter-tractable algorithms on planar graphs, for multiple reasons: branchwidth may be more tightly bounded by a function of the parameter of interest than the bounds on treewidth, it can be computed exactly in polynomial time rather than merely approximated, and the algorithm for computing it has no large hidden constants.

Generalization to matroids

It is also possible to define a notion of branch-decomposition for matroids that generalizes branch-decompositions of graphs.^[8] A branch-decomposition of a matroid is a hierarchical clustering of the matroid elements, represented as an unrooted binary tree with the elements of the matroid at its leaves. An e-separation may be defined in the same way as for graphs, and results in a partition of the set M of matroid elements into two subsets A and B. If ρ denotes the rank function of the matroid, then the width of an e-separation is defined as ρ(A) + ρ(B) − ρ(M) + 1, and the width of the decomposition and the branchwidth of the matroid are defined analogously. The branchwidth of a graph and the branchwidth of the corresponding graphic matroid may differ: for instance, the three-edge path graph and the three-edge star have different branchwidths, 2 and 1 respectively, but they both induce the same graphic matroid with branchwidth 1.^[9] However, for graphs that are not trees, the branchwidth of the graph is equal to the branchwidth of its associated graphic matroid.^[10] The branchwidth of a matroid is equal to the branchwidth of its dual matroid, and in particular this implies that the branchwidth of any planar graph that is not a tree is equal to that of its dual.^[9]

Branchwidth is an important component of attempts to extend the theory of graph minors to matroid minors: although treewidth can also be generalized to matroids,^[11] and plays a bigger role than branchwidth in the theory of graph minors, branchwidth has more convenient properties in the matroid setting.^[12] Robertson and Seymour conjectured that the matroids representable over any particular finite field are well-quasi-ordered, analogously to the Robertson–Seymour theorem for graphs, but so far this has been proven only for the matroids of bounded branchwidth.^[13] Additionally, if a minor-closed family of matroids representable over a finite field does not include the graphic matroids of all planar graphs, then there is a constant bound on the branchwidth of the matroids in the family, generalizing similar results for minor-closed graph families.^[14]

For any fixed constant k, the matroids with branchwidth at most k can be recognized in polynomial time by an algorithm that has access to the matroid via an independence oracle.^[15]

Forbidden minors

By the Robertson–Seymour theorem, the graphs of branchwidth k can be characterized by a finite set of forbidden minors. The graphs of branchwidth 0 are the matchings; the minimal forbidden minors are a two-edge path graph and a triangle graph (or the two-edge cycle, if multigraphs rather than simple graphs are considered).^[16] The graphs of branchwidth 1 are the graphs in which each connected component is a star; the minimal forbidden minors for branchwidth 1 are the triangle graph (or the two-edge cycle, if multigraphs rather than simple graphs are considered) and the three-edge path graph.^[16] The graphs of branchwidth 2 are the graphs in which each biconnected component is a series–parallel graph; the only minimal forbidden minor is the complete graph K₄ on four vertices.^[16] A graph has branchwidth three if and only if it has treewidth three and does not have the cube graph as a minor; therefore, the four minimal forbidden minors are three of the four forbidden minors for treewidth three (the graph of the octahedron, the complete graph K₅, and the Wagner graph) together with the cube graph.^[17]

Forbidden minors have also been studied for matroid branchwidth, despite the lack of a full analogue to the Robertson–Seymour theorem in this case. A matroid has branchwidth one if and only if every element is either a loop or a coloop, so the unique minimal forbidden minor is the uniform matroid U(2,3), the graphic matroid of the triangle graph. A matroid has branchwidth two if and only if it is the graphic matroid of a graph of branchwidth two, so its minimal forbidden minors are the graphic matroid of K₄ and the non-graphic matroid U(2,4). The matroids of branchwidth three are not well-quasi-ordered without the additional assumption of representability over a finite field, but nevertheless the matroids with any finite bound on their branchwidth have finitely many minimal forbidden minors, all of which have a number of elements that is at most exponential in the branchwidth.^[18]

Notes

↑ Robertson & Seymour 1991, Theorem 5.1, p. 168.
1 2 3 Seymour & Thomas (1994).
↑ Robertson & Seymour (1991), Theorem 4.1, p. 164.
↑ Bodlaender & Thilikos (1997). Fomin, Mazoit & Todinca (2009) describe an algorithm with improved dependence on k, (2√3)^k, at the expense of an increase in the dependence on the number of vertices from linear to quadratic.
↑ Kao, Ming-Yang, ed. (2008), "Treewidth of graphs", Encyclopedia of Algorithms, Springer, p. 969, ISBN 9780387307701, Another long-standing open problem is whether there is a polynomial-time algorithm to compute the treewidth of planar graphs.
↑ Gu & Tamaki (2008).
↑ Hicks (2000); Hliněný (2003).
↑ Robertson & Seymour 1991. Section 12, "Tangles and Matroids", pp. 188–190.
1 2 Mazoit & Thomassé (2007).
↑ Mazoit & Thomassé (2007); Hicks & McMurray (2007).
↑ Hliněný & Whittle (2006).
↑ Geelen, Gerards & Whittle (2006).
↑ Geelen, Gerards & Whittle (2002); Geelen, Gerards & Whittle (2006).
↑ Geelen, Gerards & Whittle (2006); Geelen, Gerards & Whittle (2007).
↑ Oum & Seymour (2007).
1 2 3 Robertson & Seymour (1991), Theorem 4.2, p. 165.
↑ Bodlaender & Thilikos (1999). The fourth forbidden minor for treewidth three, the pentagonal prism, has the cube graph as a minor, so it is not minimal for branchwidth three.
↑ Hall et al. (2002); Geelen et al. (2003).

Related Research Articles

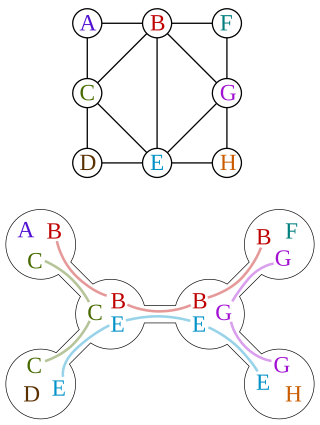
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to define the treewidth of the graph and speed up solving certain computational problems on the graph.

In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering. Equivalently, every family of graphs that is closed under minors can be defined by a finite set of forbidden minors, in the same way that Wagner's theorem characterizes the planar graphs as being the graphs that do not have the complete graph K₅ or the complete bipartite graph K_3,3 as minors.

In graph theory, an undirected graph $H$ is called a minor of the graph $G$ if $H$ can be formed from $G$ by deleting edges, vertices and by contracting edges.

In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into three-dimensional Euclidean space in such a way that no two cycles of the graph are linked. A flat embedding is an embedding with the property that every cycle is the boundary of a topological disk whose interior is disjoint from the graph. A linklessly embeddable graph is a graph that has a linkless or flat embedding; these graphs form a three-dimensional analogue of the planar graphs. Complementarily, an intrinsically linked graph is a graph that does not have a linkless embedding.

The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.

In graph theory, the Hadwiger number of an undirected graph $G$ is the size of the largest complete graph that can be obtained by contracting edges of $G$ . Equivalently, the Hadwiger number $h (G)$ is the largest number $n$ for which the complete graph $K n$ is a minor of $G$ , a smaller graph obtained from $G$ by edge contractions and vertex and edge deletions. The Hadwiger number is also known as the contraction clique number of $G$ or the homomorphism degree of $G$ . It is named after Hugo Hadwiger, who introduced it in 1943 in conjunction with the Hadwiger conjecture, which states that the Hadwiger number is always at least as large as the chromatic number of $G$ .

In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly $k$ are called $k$ -trees, and the graphs with treewidth at most $k$ are called partial $k$ -trees. Many other well-studied graph families also have bounded treewidth.

In graph theory, a path decomposition of a graph $G$ is, informally, a representation of $G$ as a "thickened" path graph, and the pathwidth of $G$ is a number that measures how much the path was thickened to form $G$ . More formally, a path-decomposition is a sequence of subsets of vertices of $G$ such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

In graph theory, series–parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.

In graph theory, a branch of mathematics, many important families of graphs can be described by a finite set of individual graphs that do not belong to the family and further exclude all graphs from the family which contain any of these forbidden graphs as (induced) subgraph or minor.

In graph theory, the clique-width of a graph $G$ is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct $G$ by means of the following 4 operations :

Creation of a new vertex $v$ with label $i$ (denoted by $i (v)$ )
Disjoint union of two labeled graphs $G$ and $H$ (denoted by $)$
Joining by an edge every vertex labeled $i$ to every vertex labeled $j$ (denoted by $η (i, j)$ ), where $i \neq j$
Renaming label $i$ to label $j$ (denoted by $ρ (i, j)$ )

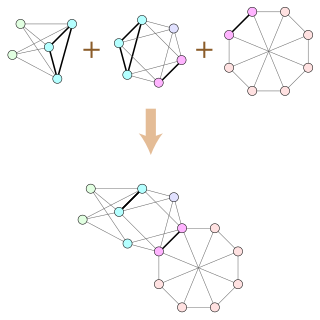
<span class="mw-page-title-main">Clique-sum</span> Gluing graphs at complete subgraphs

In graph theory, a branch of mathematics, a clique sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology. If two graphs G and H each contain cliques of equal size, the clique-sum of G and H is formed from their disjoint union by identifying pairs of vertices in these two cliques to form a single shared clique, and then deleting all the clique edges or possibly deleting some of the clique edges. A k-clique-sum is a clique-sum in which both cliques have exactly k vertices. One may also form clique-sums and k-clique-sums of more than two graphs, by repeated application of the clique-sum operation.

In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of $vertices from an n -vertex graph can partition the graph into disjoint subgraphs each of which has at most vertices.$

In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and Paul Seymour. Its proof is very long and involved. Kawarabayashi & Mohar (2007) and Lovász (2006) are surveys accessible to nonspecialists, describing the theorem and its consequences.

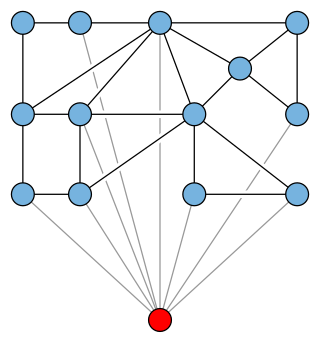
In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. It is an apex, not the apex because an apex graph may have more than one apex; for example, in the minimal nonplanar graphs $K 5$ or $K 3,3$ , every vertex is an apex. The apex graphs include graphs that are themselves planar, in which case again every vertex is an apex. The null graph is also counted as an apex graph even though it has no vertex to remove.

In the study of graph algorithms, Courcelle's theorem is the statement that every graph property definable in the monadic second-order logic of graphs can be decided in linear time on graphs of bounded treewidth. The result was first proved by Bruno Courcelle in 1990 and independently rediscovered by Borie, Parker & Tovey (1992). It is considered the archetype of algorithmic meta-theorems.

In graph theory, a bramble for an undirected graph $G$ is a family of connected subgraphs of $G$ that all touch each other: for every pair of disjoint subgraphs, there must exist an edge in $G$ that has one endpoint in each subgraph. The order of a bramble is the smallest size of a hitting set, a set of vertices of $G$ that has a nonempty intersection with each of the subgraphs. Brambles may be used to characterize the treewidth of $G$ .

In the mathematical theory of matroids, a minor of a matroid M is another matroid N that is obtained from M by a sequence of restriction and contraction operations. Matroid minors are closely related to graph minors, and the restriction and contraction operations by which they are formed correspond to edge deletion and edge contraction operations in graphs. The theory of matroid minors leads to structural decompositions of matroids, and characterizations of matroid families by forbidden minors, analogous to the corresponding theory in graphs.

<span class="mw-page-title-main">Planar cover</span>

In graph theory, a planar cover of a finite graph G is a finite covering graph of G that is itself a planar graph. Every graph that can be embedded into the projective plane has a planar cover; an unsolved conjecture of Seiya Negami states that these are the only graphs with planar covers.

In graph theory, the carving width of a graph is a number, defined from the graph, that describes the number of edges separating the clusters in a hierarchical clustering of the graph vertices.

References

Bodlaender, Hans L.; Thilikos, Dimitrios M. (1997), "Constructive linear time algorithms for branchwidth", Proc. 24th International Colloquium on Automata, Languages and Programming (ICALP '97), Lecture Notes in Computer Science, vol. 1256, Springer-Verlag, pp. 627–637, doi:10.1007/3-540-63165-8_217, hdl:2117/96447 .
Bodlaender, Hans L.; Thilikos, Dimitrios M. (1999), "Graphs with branchwidth at most three", Journal of Algorithms, 32 (2): 167–194, doi:10.1006/jagm.1999.1011 .
Cook, William; Seymour, Paul D. (2003), "Tour merging via branch-decomposition" (PDF), INFORMS Journal on Computing, 15 (3): 233–248, doi:10.1287/ijoc.15.3.233.16078 .
Fomin, Fedor V.; Thilikos, Dimitrios M. (2006), "Dominating sets in planar graphs: branch-width and exponential speed-up", SIAM Journal on Computing, 36 (2): 281, doi:10.1137/S0097539702419649 .
Fomin, Fedor V.; Mazoit, Frédéric; Todinca, Ioan (2009), "Computing branchwidth via efficient triangulations and blocks", Discrete Applied Mathematics, 157 (12): 2726–2736, doi:10.1016/j.dam.2008.08.009 .
Geelen, Jim; Gerards, Bert; Robertson, Neil; Whittle, Geoff (2003), "On the excluded minors for the matroids of branch-width k", Journal of Combinatorial Theory, Series B, 88 (2): 261–265, doi: 10.1016/S0095-8956(02)00046-1 .
Geelen, Jim; Gerards, Bert; Whittle, Geoff (2002), "Branch-width and well-quasi-ordering in matroids and graphs", Journal of Combinatorial Theory, Series B, 84 (2): 270–290, doi:10.1006/jctb.2001.2082 .
Geelen, Jim; Gerards, Bert; Whittle, Geoff (2006), "Towards a structure theory for matrices and matroids" (PDF), Proc. International Congress of Mathematicians , vol. III, pp. 827–842.
Geelen, Jim; Gerards, Bert; Whittle, Geoff (2007), "Excluding a planar graph from GF(q)-representable matroids" (PDF), Journal of Combinatorial Theory, Series B, 97 (6): 971–998, doi:10.1016/j.jctb.2007.02.005, archived from the original (PDF) on 2010-09-24.
Gu, Qian-Ping; Tamaki, Hisao (July 2008), "Optimal branch-decomposition of planar graphs in O(n³) time", ACM Transactions on Algorithms, 4 (3): 30:1–30:13, doi:10.1145/1367064.1367070 .
Hall, Rhiannon; Oxley, James; Semple, Charles; Whittle, Geoff (2002), "On matroids of branch-width three", Journal of Combinatorial Theory, Series B, 86 (1): 148–171, doi:10.1006/jctb.2002.2120 .
Hicks, Illya V. (2000), Branch Decompositions and their Applications, Ph.D. thesis, Rice University, archived from the original on 2011-07-16, retrieved 2010-07-06.
Hicks, Illya V.; McMurray, Nolan B. Jr. (2007), "The branchwidth of graphs and their cycle matroids", Journal of Combinatorial Theory, Series B, 97 (5): 681–692, doi:10.1016/j.jctb.2006.12.007 .
Hliněný, Petr (2003), "On matroid properties definable in the MSO logic", Proc. 28th International Symposium on Mathematical Foundations of Computer Science (MFCS '03), Lecture Notes in Computer Science, vol. 2747, Springer-Verlag, pp. 470–479, doi:10.1007/978-3-540-45138-9\_41
Hliněný, Petr; Whittle, Geoff (2006), "Matroid tree-width" (PDF), European Journal of Combinatorics, 27 (7): 1117–1128, doi:10.1016/j.ejc.2006.06.005, archived from the original (PDF) on 2012-03-06, retrieved 2010-07-06
.
- Addendum and corrigendum: Hliněný, Petr; Whittle, Geoff (2009), "Addendum to matroid tree-width", European Journal of Combinatorics, 30 (4): 1036–1044, doi: 10.1016/j.ejc.2008.09.028 .
Mazoit, Frédéric; Thomassé, Stéphan (2007), "Branchwidth of graphic matroids", in Hilton, Anthony; Talbot, John (eds.), Surveys in Combinatorics 2007 (PDF), London Mathematical Society Lecture Note Series, vol. 346, Cambridge University Press, p. 275.
Oum, Sang-il; Seymour, Paul (2007), "Testing branch-width", Journal of Combinatorial Theory , Series B, 97 (3): 385–393, doi:10.1016/j.jctb.2006.06.006, MR 2305892 .
Robertson, Neil; Seymour, Paul D. (1991), "Graph minors. X. Obstructions to tree-decomposition", Journal of Combinatorial Theory, 52 (2): 153–190, doi:10.1016/0095-8956(91)90061-N .
Seymour, Paul D.; Thomas, Robin (1994), "Call routing and the ratcatcher", Combinatorica, 14 (2): 217–241, doi:10.1007/BF01215352 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Robertson & Seymour 1991, Theorem 5.1, p. 168.

[st94-2] 1 2 3 Seymour & Thomas (1994).

[3] Robertson & Seymour (1991), Theorem 4.1, p. 164.

[4] Bodlaender & Thilikos (1997). Fomin, Mazoit & Todinca (2009) describe an algorithm with improved dependence on k, (2√3)^k, at the expense of an increase in the dependence on the number of vertices from linear to quadratic.

[5] Kao, Ming-Yang, ed. (2008), "Treewidth of graphs", Encyclopedia of Algorithms, Springer, p. 969, ISBN 9780387307701, Another long-standing open problem is whether there is a polynomial-time algorithm to compute the treewidth of planar graphs.

[FOOTNOTEGuTamaki2008-6] Gu & Tamaki (2008).

[7] Hicks (2000); Hliněný (2003).

[8] Robertson & Seymour 1991. Section 12, "Tangles and Matroids", pp. 188–190.

[mt07-9] 1 2 Mazoit & Thomassé (2007).

[10] Mazoit & Thomassé (2007); Hicks & McMurray (2007).

[11] Hliněný & Whittle (2006).

[12] Geelen, Gerards & Whittle (2006).

[13] Geelen, Gerards & Whittle (2002); Geelen, Gerards & Whittle (2006).

[14] Geelen, Gerards & Whittle (2006); Geelen, Gerards & Whittle (2007).

[15] Oum & Seymour (2007).

[rs91-4.2-16] 1 2 3 Robertson & Seymour (1991), Theorem 4.2, p. 165.

[17] Bodlaender & Thilikos (1999). The fourth forbidden minor for treewidth three, the pentagonal prism, has the cube graph as a minor, so it is not minimal for branchwidth three.

[18] Hall et al. (2002); Geelen et al. (2003).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]