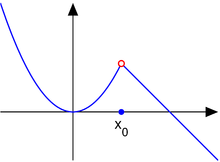
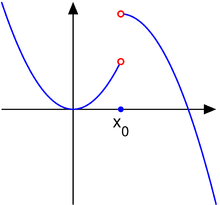
In mathematics, specifically in measure theory, a Borel measure on a topological space is a measure that is defined on all open sets. Some authors require additional restrictions on the measure, as described below.
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as discontinuities. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is not continuous. Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity.
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a function whose domain is a directed set. The codomain of this function is usually some topological space. Nets directly generalize the concept of a sequence in a metric space. Nets are primarily used in the fields of Analysis and Topology, where they are used to characterize many important topological properties that, sequences are unable to characterize. Nets are in one-to-one correspondence with filters.

In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. It was presented to the faculty at the University of Göttingen in 1854, but not published in a journal until 1868. For many functions and practical applications, the Riemann integral can be evaluated by the fundamental theorem of calculus or approximated by numerical integration, or simulated using Monte Carlo integration.
In mathematics, the branch of real analysis studies the behavior of real numbers, sequences and series of real numbers, and real functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.
In mathematics, and in particular measure theory, a measurable function is a function between the underlying sets of two measurable spaces that preserves the structure of the spaces: the preimage of any measurable set is measurable. This is in direct analogy to the definition that a continuous function between topological spaces preserves the topological structure: the preimage of any open set is open. In real analysis, measurable functions are used in the definition of the Lebesgue integral. In probability theory, a measurable function on a probability space is known as a random variable.
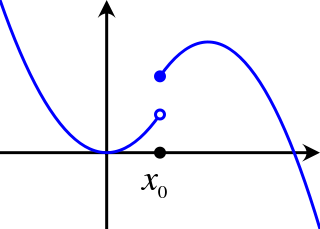
In mathematical analysis, semicontinuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function is uppersemicontinuous at a point if, roughly speaking, the function values for arguments near are not much higher than
In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input which may or may not be in the domain of the function.
In mathematics, Fatou's lemma establishes an inequality relating the Lebesgue integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions. The lemma is named after Pierre Fatou.

In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A differentiable function is smooth and does not contain any break, angle, or cusp.
In mathematical analysis, a function of bounded variation, also known as BV function, is a real-valued function whose total variation is bounded (finite): the graph of a function having this property is well behaved in a precise sense. For a continuous function of a single variable, being of bounded variation means that the distance along the direction of the y-axis, neglecting the contribution of motion along x-axis, traveled by a point moving along the graph has a finite value. For a continuous function of several variables, the meaning of the definition is the same, except for the fact that the continuous path to be considered cannot be the whole graph of the given function, but can be every intersection of the graph itself with a hyperplane parallel to a fixed x-axis and to the y-axis.
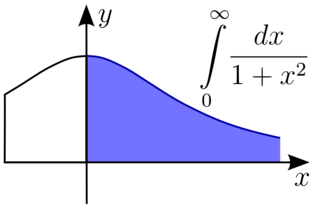
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals, this typically involves unboundedness, either of the set over which the integral is taken or of the integrand, or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral is worked out as if it is improper, the same answer will result.
In functional analysis, it is often convenient to define a linear transformation on a complete, normed vector space by first defining a linear transformation on a dense subset of and then continuously extending to the whole space via the theorem below. The resulting extension remains linear and bounded, and is thus continuous, which makes it a continuous linear extension.

In mathematics, the oscillation of a function or a sequence is a number that quantifies how much that sequence or function varies between its extreme values as it approaches infinity or a point. As is the case with limits, there are several definitions that put the intuitive concept into a form suitable for a mathematical treatment: oscillation of a sequence of real numbers, oscillation of a real-valued function at a point, and oscillation of a function on an interval.
In mathematics, the Dirichlet function is the indicator function of the set of rational numbers , i.e. if x is a rational number and if x is not a rational number.
In the branch of mathematics known as real analysis, the Darboux integral is constructed using Darboux sums and is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of the two integrals, if they exist, are equal. The definition of the Darboux integral has the advantage of being easier to apply in computations or proofs than that of the Riemann integral. Consequently, introductory textbooks on calculus and real analysis often develop Riemann integration using the Darboux integral, rather than the true Riemann integral. Moreover, the definition is readily extended to defining Riemann–Stieltjes integration. Darboux integrals are named after their inventor, Gaston Darboux (1842–1917).

Thomae's function is a real-valued function of a real variable that can be defined as:

In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the X axis. The Lebesgue integral, named after French mathematician Henri Lebesgue, extends the integral to a larger class of functions. It also extends the domains on which these functions can be defined.
In mathematics, a limit is the value that a function approaches as the input approaches some value. Limits are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals.