In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.
In mathematics, the branch of real analysis studies the behavior of real numbers, sequences and series of real numbers, and real functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.
In mathematics, the tangent space of a manifold is a generalization of tangent lines to curves in two-dimensional space and tangent planes to surfaces in three-dimensional space in higher dimensions. In the context of physics the tangent space to a manifold at a point can be viewed as the space of possible velocities for a particle moving on the manifold.

In calculus, Taylor's theorem gives an approximation of a -times differentiable function around a given point by a polynomial of degree , called the -th-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation at the order of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation. There are several versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial.

In mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: there exists a real number such that, for every pair of points on the graph of this function, the absolute value of the slope of the line connecting them is not greater than this real number; the smallest such bound is called the Lipschitz constant of the function. For instance, every function that is defined on an interval and has a bounded first derivative is Lipschitz continuous.
Distributions, also known as Schwartz distributions or generalized functions, are objects that generalize the classical notion of functions in mathematical analysis. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative.

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions.

In mathematics, a curve is an object similar to a line, but that does not have to be straight.
In differential geometry, a Riemannian manifold or Riemannian space(M, g), so called after the German mathematician Bernhard Riemann, is a real, smooth manifold M equipped with a positive-definite inner product gp on the tangent space TpM at each point p.
In mathematics, a diffeology on a set generalizes the concept of smooth charts in a differentiable manifold, declaring what the "smooth parametrizations" in the set are.

In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A differentiable function is smooth and does not contain any break, angle, or cusp.
In mathematics, the notion of a germ of an object in/on a topological space is an equivalence class of that object and others of the same kind that captures their shared local properties. In particular, the objects in question are mostly functions and subsets. In specific implementations of this idea, the functions or subsets in question will have some property, such as being analytic or smooth, but in general this is not needed ; it is however necessary that the space on/in which the object is defined is a topological space, in order that the word local has some meaning.
In mathematics, smooth functions and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument is smooth. The converse is not true, as demonstrated with the counterexample below.
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function together with its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, i.e. a Banach space. Intuitively, a Sobolev space is a space of functions possessing sufficiently many derivatives for some application domain, such as partial differential equations, and equipped with a norm that measures both the size and regularity of a function.
Multivariable calculus is the extension of calculus in one variable to calculus with functions of several variables: the differentiation and integration of functions involving multiple variables (multivariate), rather than just one.

In mathematics, a bump function is a function on a Euclidean space which is both smooth and compactly supported. The set of all bump functions with domain forms a vector space, denoted or The dual space of this space endowed with a suitable topology is the space of distributions.

In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible, then computations done in one chart are valid in any other differentiable chart.
In mathematics, convenient vector spaces are locally convex vector spaces satisfying a very mild completeness condition.
In the mathematical discipline of functional analysis, a differentiable vector-valued function from Euclidean space is a differentiable function valued in a topological vector space (TVS) whose domains is a subset of some finite-dimensional Euclidean space. It is possible to generalize the notion of derivative to functions whose domain and codomain are subsets of arbitrary topological vector spaces (TVSs) in multiple ways. But when the domain of a TVS-valued function is a subset of a finite-dimensional Euclidean space then many of these notions become logically equivalent resulting in a much more limited number of generalizations of the derivative and additionally, differentiability is also more well-behaved compared to the general case. This article presents the theory of -times continuously differentiable functions on an open subset of Euclidean space , which is an important special case of differentiation between arbitrary TVSs. This importance stems partially from the fact that every finite-dimensional vector subspace of a Hausdorff topological vector space is TVS isomorphic to Euclidean space so that, for example, this special case can be applied to any function whose domain is an arbitrary Hausdorff TVS by restricting it to finite-dimensional vector subspaces.
In mathematics, calculus on Euclidean space is a generalization of calculus of functions in one or several variables to calculus of functions on Euclidean space as well as a finite-dimensional real vector space. This calculus is also known as advanced calculus, especially in the United States. It is similar to multivariable calculus but is somewhat more sophisticated in that it uses linear algebra more extensively and covers some concepts from differential geometry such as differential forms and Stokes' formula in terms of differential forms. This extensive use of linear algebra also allows a natural generalization of multivariable calculus to calculus on Banach spaces or topological vector spaces.























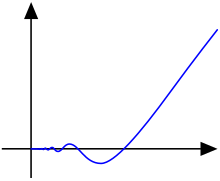
![The function
f
:
R
-
R
{\displaystyle f:\mathbb {R} \to \mathbb {R} }
with
f
(
x
)
=
x
2
sin
[?]
(
1
x
)
{\displaystyle f(x)=x^{2}\sin \left({\tfrac {1}{x}}\right)}
for
x
[?]
0
{\displaystyle x\neq 0}
and
f
(
0
)
=
0
{\displaystyle f(0)=0}
is differentiable. However, this function is not continuously differentiable. The function x^2*sin(1 over x).svg](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6b/The_function_x%5E2%2Asin%281_over_x%29.svg/290px-The_function_x%5E2%2Asin%281_over_x%29.svg.png)