
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology, algebraic geometry and differential geometry behave as they "run round" a singularity. As the name implies, the fundamental meaning of monodromy comes from "running round singly". It is closely associated with covering maps and their degeneration into ramification; the aspect giving rise to monodromy phenomena is that certain functions we may wish to define fail to be single-valued as we "run round" a path encircling a singularity. The failure of monodromy can be measured by defining a monodromy group: a group of transformations acting on the data that encodes what happens as we "run round" in one dimension. Lack of monodromy is sometimes called polydromy.

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space : to every point of the space we associate a vector space in such a way that these vector spaces fit together to form another space of the same kind as , which is then called a vector bundle over .

In mathematics, and particularly topology, a fiber bundle is a space that is locally a product space, but globally may have a different topological structure. Specifically, the similarity between a space and a product space is defined using a continuous surjective map, that in small regions of behaves just like a projection from corresponding regions of to The map called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space is known as the total space of the fiber bundle, as the base space, and the fiber.
In mathematics, a Lie algebroid is a vector bundle together with a Lie bracket on its space of sections and a vector bundle morphism , satisfying a Leibniz rule. A Lie algebroid can thus be thought of as a "many-object generalisation" of a Lie algebra.
In mathematics, a principal bundle is a mathematical object that formalizes some of the essential features of the Cartesian product of a space with a group . In the same way as with the Cartesian product, a principal bundle is equipped with
- An action of on , analogous to for a product space.
- A projection onto . For a product space, this is just the projection onto the first factor, .
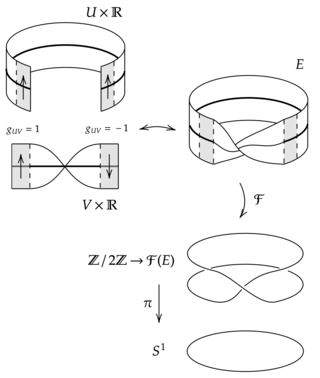
In mathematics, a frame bundle is a principal fiber bundle F(E) associated to any vector bundle E. The fiber of F(E) over a point x is the set of all ordered bases, or frames, for Ex. The general linear group acts naturally on F(E) via a change of basis, giving the frame bundle the structure of a principal GL(k, R)-bundle (where k is the rank of E).

In the mathematical field of topology, a section of a fiber bundle is a continuous right inverse of the projection function . In other words, if is a fiber bundle over a base space, :

In mathematics, a foliation is an equivalence relation on an n-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension p, modeled on the decomposition of the real coordinate space Rn into the cosets x + Rp of the standardly embedded subspace Rp. The equivalence classes are called the leaves of the foliation. If the manifold and/or the submanifolds are required to have a piecewise-linear, differentiable, or analytic structure then one defines piecewise-linear, differentiable, or analytic foliations, respectively. In the most important case of differentiable foliation of class Cr it is usually understood that r ≥ 1. The number p is called the dimension of the foliation and q = n − p is called its codimension.
In mathematics, and especially differential geometry and gauge theory, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. The most common case is that of a linear connection on a vector bundle, for which the notion of parallel transport must be linear. A linear connection is equivalently specified by a covariant derivative, an operator that differentiates sections of the bundle along tangent directions in the base manifold, in such a way that parallel sections have derivative zero. Linear connections generalize, to arbitrary vector bundles, the Levi-Civita connection on the tangent bundle of a pseudo-Riemannian manifold, which gives a standard way to differentiate vector fields. Nonlinear connections generalize this concept to bundles whose fibers are not necessarily linear.
In mathematics, and especially differential geometry and gauge theory, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. A principal G-connection on a principal G-bundle over a smooth manifold is a particular type of connection which is compatible with the action of the group .
This is a glossary of terms specific to differential geometry and differential topology. The following three glossaries are closely related:
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms.
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a principal G-subbundle of the tangent frame bundle FM (or GL(M)) of M.
In mathematics, a pullback bundle or induced bundle is the fiber bundle that is induced by a map of its base-space. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′. The fiber of f*E over a point b′ in B′ is just the fiber of E over f(b′). Thus f*E is the disjoint union of all these fibers equipped with a suitable topology.
In differential geometry, in the category of differentiable manifolds, a fibered manifold is a surjective submersion
In mathematical physics, covariant classical field theory represents classical fields by sections of fiber bundles, and their dynamics is phrased in the context of a finite-dimensional space of fields. Nowadays, it is well known that jet bundles and the variational bicomplex are the correct domain for such a description. The Hamiltonian variant of covariant classical field theory is the covariant Hamiltonian field theory where momenta correspond to derivatives of field variables with respect to all world coordinates. Non-autonomous mechanics is formulated as covariant classical field theory on fiber bundles over the time axis ℝ.
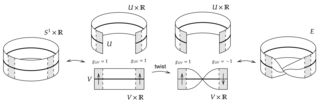
In mathematics, the fiber bundle construction theorem is a theorem which constructs a fiber bundle from a given base space, fiber and a suitable set of transition functions. The theorem also gives conditions under which two such bundles are isomorphic. The theorem is important in the associated bundle construction where one starts with a given bundle and surgically replaces the fiber with a new space while keeping all other data the same.
In topology, a branch of mathematics, the clutching construction is a way of constructing fiber bundles, particularly vector bundles on spheres.
In mathematics, an adjoint bundle is a vector bundle naturally associated to any principal bundle. The fibers of the adjoint bundle carry a Lie algebra structure making the adjoint bundle into a (nonassociative) algebra bundle. Adjoint bundles have important applications in the theory of connections as well as in gauge theory.
In mathematics, and especially differential geometry and mathematical physics, gauge theory is the general study of connections on vector bundles, principal bundles, and fibre bundles. Gauge theory in mathematics should not be confused with the closely related concept of a gauge theory in physics, which is a field theory which admits gauge symmetry. In mathematics theory means a mathematical theory, encapsulating the general study of a collection of concepts or phenomena, whereas in the physical sense a gauge theory is a mathematical model of some natural phenomenon.




























