
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success or failure. A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.
In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter. For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. So, two combinations are identical if and only if each combination has the same members. If the set has n elements, the number of k-combinations, denoted by or , is equal to the binomial coefficient
A poker player is drawing if they have a hand that is incomplete and needs further cards to become valuable. The hand itself is called a draw or drawing hand. For example, in seven-card stud, if four of a player's first five cards are all spades, but the hand is otherwise weak, they are drawing to a flush. In contrast, a made hand already has value and does not necessarily need to draw to win. A made starting hand with no help can lose to an inferior starting hand with a favorable draw. If an opponent has a made hand that will beat the player's draw, then the player is drawing dead; even if they make their desired hand, they will lose. Not only draws benefit from additional cards; many made hands can be improved by catching an out – and may have to in order to win.
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference.
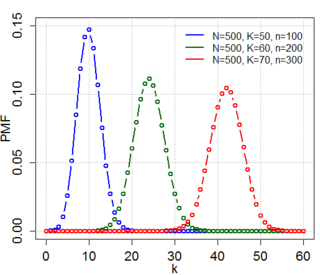
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of successes in draws, without replacement, from a finite population of size that contains exactly objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of successes in draws with replacement.
In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

In combinatorics, a branch of mathematics, the inclusion–exclusion principle is a counting technique which generalizes the familiar method of obtaining the number of elements in the union of two finite sets; symbolically expressed as
A prior probability distribution of an uncertain quantity, often simply called the prior, is its assumed probability distribution before some evidence is taken into account. For example, the prior could be the probability distribution representing the relative proportions of voters who will vote for a particular politician in a future election. The unknown quantity may be a parameter of the model or a latent variable rather than an observable variable.
Fisher's exact test is a statistical significance test used in the analysis of contingency tables. Although in practice it is employed when sample sizes are small, it is valid for all sample sizes. It is named after its inventor, Ronald Fisher, and is one of a class of exact tests, so called because the significance of the deviation from a null hypothesis can be calculated exactly, rather than relying on an approximation that becomes exact in the limit as the sample size grows to infinity, as with many statistical tests.
Charles Anderson Worsley Anderson-Pelham, 2nd Earl of Yarborough was a British nobleman who succeeded to the Earldom of Yarborough in 1846.
In statistics, the method of moments is a method of estimation of population parameters. The same principle is used to derive higher moments like skewness and kurtosis.
In contract bridge, the principle of restricted choice states that "The play of a card which may have been selected as a choice of equal plays increases the chance that the player started with a holding in which his choice was restricted." Crucially, it helps play "in situations which used to be thought of as guesswork."
These terms are used in contract bridge, using duplicate or rubber scoring. Some of them are also used in whist, bid whist, the obsolete game auction bridge, and other trick-taking games. This glossary supplements the Glossary of card game terms.
In the card game contract bridge, a suit combination is a specific subset of the cards of one suit held respectively in declarer's and dummy's hands at the onset of play. While the ranks of the remaining cards held by the defenders can be deduced precisely, their location is unknown. Optimum suit combination play allows for all possible lies of the cards held by the defenders.
A balanced hand or balanced distribution in card games is a hand with an even distribution of suits. In the game of contract bridge, it denotes a hand of thirteen cards which contains no singleton or void and at most one doubleton. Three hand patterns are classified as truly balanced: 4-3-3-3, 4-4-3-2 and 5-3-3-2. The hand patterns 5-4-2-2 and 6-3-2-2 are generally referred to as semi-balanced.

In the statistical theory of estimation, the German tank problem consists of estimating the maximum of a discrete uniform distribution from sampling without replacement. In simple terms, suppose there exists an unknown number of items which are sequentially numbered from 1 to N. A random sample of these items is taken and their sequence numbers observed; the problem is to estimate N from these observed numbers.
Bridge base basic, also known as BBO basic, is a bidding system for the game of bridge based on the Standard American Yellow Card (SAYC). It is simplified, suitable for beginners, and widely used in internet bridge, particularly on Bridge Base Online. It is taught in Fred Gitelman's educational software called Learn to Play Bridge that is available as a free download from the American Contract Bridge League's website.
In the card game bridge, the law or principle of vacant places is a simple method for estimating the probable location of any particular card in the two unseen hands. It can be used both to aid in a decision at the table and to derive the entire suit division probability table.
In contract bridge, the honor point count is a system for hand evaluation.
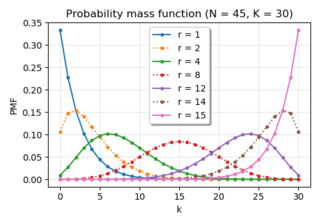
In probability theory and statistics, the negative hypergeometric distribution describes probabilities for when sampling from a finite population without replacement in which each sample can be classified into two mutually exclusive categories like Pass/Fail or Employed/Unemployed. As random selections are made from the population, each subsequent draw decreases the population causing the probability of success to change with each draw. Unlike the standard hypergeometric distribution, which describes the number of successes in a fixed sample size, in the negative hypergeometric distribution, samples are drawn until failures have been found, and the distribution describes the probability of finding successes in such a sample. In other words, the negative hypergeometric distribution describes the likelihood of successes in a sample with exactly failures.





















