
In mathematics, an n-sphere or hypersphere is an n-dimensional generalization of the 1-dimensional circle and 2-dimensional sphere to any non-negative integer n. The n-sphere is the setting for n-dimensional spherical geometry.

In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.

In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined intrinsically without reference to a larger space.
In mechanics and geometry, the 3D rotation group, often denoted O(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric tensor on M consists of a metric tensor at each point p of M that varies smoothly with p.

In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane, denoted below as H, together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry.

In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.
In mathematics, a Killing vector field, named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold. More simply, the flow generates a symmetry, in the sense that moving each point of an object the same distance in the direction of the Killing vector will not distort distances on the object.
The Kerr–Newman metric is the most general asymptotically flat and stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged and rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions; that is, it is a solution to the Einstein–Maxwell equations that account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions.
In probability and statistics, a circular distribution or polar distribution is a probability distribution of a random variable whose values are angles, usually taken to be in the range [0, 2π). A circular distribution is often a continuous probability distribution, and hence has a probability density, but such distributions can also be discrete, in which case they are called circular lattice distributions. Circular distributions can be used even when the variables concerned are not explicitly angles: the main consideration is that there is not usually any real distinction between events occurring at the opposite ends of the range, and the division of the range could notionally be made at any point.
In differential geometry, the Laplace–Beltrami operator is a generalization of the Laplace operator to functions defined on submanifolds in Euclidean space and, even more generally, on Riemannian and pseudo-Riemannian manifolds. It is named after Pierre-Simon Laplace and Eugenio Beltrami.
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates. Thus a volume element is an expression of the form
A frame field in general relativity is a set of four pointwise-orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime. The timelike unit vector field is often denoted by and the three spacelike unit vector fields by . All tensorial quantities defined on the manifold can be expressed using the frame field and its dual coframe field.
A parametric surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters :\mathbb {R} ^{2}\to \mathbb {R} ^{3}} . Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.
In the differential geometry of surfaces, a Darboux frame is a natural moving frame constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non-umbilic point of a surface embedded in Euclidean space. It is named after French mathematician Jean Gaston Darboux.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to
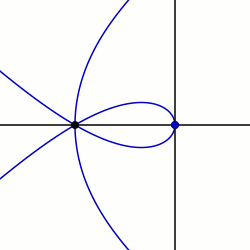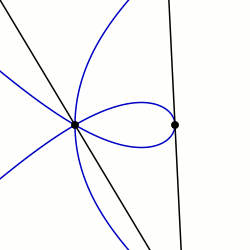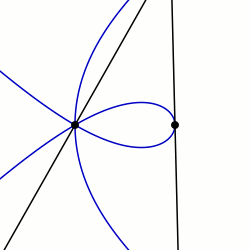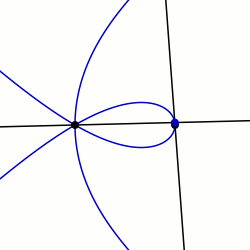
In geometry, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is linear. The name is derived from the trisectrix of Maclaurin, which is a prominent member of the family, and their sectrix property, which means they can be used to divide an angle into a given number of equal parts. There are special cases known as arachnida or araneidans because of their spider-like shape, and Plateau curves after Joseph Plateau who studied them.

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric spacetime, which is adapted to these nested round spheres. The defining characteristic of Schwarzschild chart is that the radial coordinate possesses a natural geometric interpretation in terms of the surface area and Gaussian curvature of each sphere. However, radial distances and angles are not accurately represented.
In Einstein's theory of general relativity, the interior Schwarzschild metric is an exact solution for the gravitational field in the interior of a non-rotating spherical body which consists of an incompressible fluid and has zero pressure at the surface. This is a static solution, meaning that it does not change over time. It was discovered by Karl Schwarzschild in 1916, who earlier had found the exterior Schwarzschild metric.










































