Shape of the universe

Last updated

In physical cosmology, the shape of the universe refers to both its local and global geometry. Local geometry is defined primarily by its curvature, while the global geometry is characterised by its topology (which itself is constrained by curvature). General relativity explains how spatial curvature (local geometry) is constrained by gravity. The global topology of the universe cannot be deduced from measurements of curvature inferred from observations within the family of homogeneous general relativistic models alone, due to the existence of locally indistinguishable spaces with varying global topological characteristics. For example; a multiply connected space like a 3 torus has everywhere zero curvature but is finite in extent, whereas a flat simply connected space is infinite in extent (Euclidean space).

Contents

Current observational evidence (WMAP, BOOMERanG, and Planck for example) imply that the observable universe is flat to within a 0.4% margin of error of the curvature density parameter with an unknown global topology. [1] [2] It is currently unknown if the universe is simply connected like euclidean space or multiply connected like a torus. To date, no compelling evidence has been found suggesting the universe has a non-trivial (i.e.; not simply connected) topology, though it has not been ruled out by astronomical observations.

Shape of the observable universe

The universe's structure can be examined from two angles:

  1. Local geometry: This relates to the curvature of the universe, primarily concerning what we can observe.
  2. Global geometry: This pertains to the universe's overall shape and structure.

The observable universe is a roughly spherical region extending 46.5 billion light-years in all directions from any observer. It appears older and more redshifted the deeper we look into space. In theory, we could look all the way back to the Big Bang, but in practice, we can only see up to the cosmic microwave background (CMB) (roughly 370,000 years after the big bang) as anything beyond that is opaque. Studies show that the observable universe is isotropic and homogeneous on the largest scales.

If the observable universe encompasses the entire universe, we might determine its structure through observation. However, if the observable universe is smaller, we can only grasp a portion of it, making it impossible to deduce the global geometry through observation. Different mathematical models of the universe's global geometry can be constructed, all consistent with current observations and general relativity. Hence, it is unclear whether the observable universe matches the entire universe or is significantly smaller, though it is generally accepted that the universe is larger than the observable universe.

The universe may be compact in some dimensions and not in others, similar to how a cuboid is longer in one dimension than the others. Scientists test these models by looking for novel implications – phenomena not yet observed but necessary if the model is accurate. For instance, a small closed universe would produce multiple images of the same object in the sky, though not necessarily of the same age. As of 2023 current observational evidence suggests that the observable universe is spatially flat with an unknown global structure.

Curvature of the universe

The curvature is a quantity describing how the geometry of a space differs locally from the one of the flat space. The curvature of any locally isotropic space (and hence of a locally isotropic universe) falls into one of the three following cases:

  1. Zero curvature (flat) — a drawn triangle's angles add up to 180° and the Pythagorean theorem holds; such 3-dimensional space is locally modeled by Euclidean space E3.
  2. Positive curvature — a drawn triangle's angles add up to more than 180°; such 3-dimensional space is locally modeled by a region of a 3-sphere S3.
  3. Negative curvature — a drawn triangle's angles add up to less than 180°; such 3-dimensional space is locally modeled by a region of a hyperbolic space H3.

Curved geometries are in the domain of Non-Euclidean geometry. An example of a positively curved space would be the surface of a sphere such as the Earth. A triangle drawn from the equator to a pole will have at least two angles equal 90°, which makes the sum of the 3 angles greater than 180°. An example of a negatively curved surface would be the shape of a saddle or mountain pass. A triangle drawn on a saddle surface will have the sum of the angles adding up to less than 180°.

The local geometry of the universe is determined by whether the density parameter O is greater than, less than, or equal to 1. From top to bottom: a spherical universe with O > 1, a hyperbolic universe with O < 1, and a flat universe with O = 1. These depictions of two-dimensional surfaces are merely easily visualizable analogs to the 3-dimensional structure of (local) space. End of universe.jpg
The local geometry of the universe is determined by whether the density parameter Ω is greater than, less than, or equal to 1. From top to bottom: a spherical universe with Ω > 1, a hyperbolic universe with Ω < 1, and a flat universe with Ω = 1. These depictions of two-dimensional surfaces are merely easily visualizable analogs to the 3-dimensional structure of (local) space.

General relativity explains that mass and energy bend the curvature of spacetime and is used to determine what curvature the universe has by using a value called the density parameter, represented with Omega (Ω). The density parameter is the average density of the universe divided by the critical energy density, that is, the mass energy needed for a universe to be flat. Put another way,

One can experimentally calculate this Ω to determine the curvature two ways. One is to count up all the mass–energy in the universe and take its average density then divide that average by the critical energy density. Data from Wilkinson Microwave Anisotropy Probe (WMAP) as well as the Planck spacecraft give values for the three constituents of all the mass–energy in the universe – normal mass (baryonic matter and dark matter), relativistic particles (predominantly photons and neutrinos), and dark energy or the cosmological constant: [3] [4]

Ωmass ≈ 0.315±0.018

Ωrelativistic ≈ 9.24×10−5

ΩΛ ≈ 0.6817±0.0018

Ωtotal = Ωmass + Ωrelativistic + ΩΛ = 1.00±0.02

The actual value for critical density value is measured as ρcritical = 9.47×10−27 kg m−3. From these values, within experimental error, the universe seems to be spatially flat.

Another way to measure Ω is to do so geometrically by measuring an angle across the observable universe. We can do this by using the CMB and measuring the power spectrum and temperature anisotropy. For instance, one can imagine finding a gas cloud that is not in thermal equilibrium due to being so large that light speed cannot propagate the thermal information. Knowing this propagation speed, we then know the size of the gas cloud as well as the distance to the gas cloud, we then have two sides of a triangle and can then determine the angles. Using a method similar to this, the BOOMERanG experiment has determined that the sum of the angles to 180° within experimental error, corresponding to an Ωtotal ≈ 1.00±0.12. [5]

These and other astronomical measurements constrain the spatial curvature to be very close to zero, although they do not constrain its sign. This means that although the local geometries of spacetime are generated by the theory of relativity based on spacetime intervals, we can approximate 3-space by the familiar Euclidean geometry.

The Friedmann–Lemaître–Robertson–Walker (FLRW) model using Friedmann equations is commonly used to model the universe. The FLRW model provides a curvature of the universe based on the mathematics of fluid dynamics, that is, modeling the matter within the universe as a perfect fluid. Although stars and structures of mass can be introduced into an "almost FLRW" model, a strictly FLRW model is used to approximate the local geometry of the observable universe. Another way of saying this is that if all forms of dark energy are ignored, then the curvature of the universe can be determined by measuring the average density of matter within it, assuming that all matter is evenly distributed (rather than the distortions caused by 'dense' objects such as galaxies). This assumption is justified by the observations that, while the universe is "weakly" inhomogeneous and anisotropic (see the large-scale structure of the cosmos), it is on average homogeneous and isotropic when analyzed at a sufficiently large spatial scale.

Global universe structure

Global structure covers the geometry and the topology of the whole universe—both the observable universe and beyond. While the local geometry does not determine the global geometry completely, it does limit the possibilities, particularly a geometry of a constant curvature. The universe is often taken to be a geodesic manifold, free of topological defects; relaxing either of these complicates the analysis considerably. A global geometry is a local geometry plus a topology. It follows that a topology alone does not give a global geometry: for instance, Euclidean 3-space and hyperbolic 3-space have the same topology but different global geometries.

As stated in the introduction, investigations within the study of the global structure of the universe include:

Infinite or finite

One of the unanswered questions about the universe is whether it is infinite or finite in extent. For intuition, it can be understood that a finite universe has a finite volume that, for example, could be in theory filled up with a finite amount of material, while an infinite universe is unbounded and no numerical volume could possibly fill it. Mathematically, the question of whether the universe is infinite or finite is referred to as boundedness. An infinite universe (unbounded metric space) means that there are points arbitrarily far apart: for any distance d, there are points that are of a distance at least d apart. A finite universe is a bounded metric space, where there is some distance d such that all points are within distance d of each other. The smallest such d is called the diameter of the universe, in which case the universe has a well-defined "volume" or "scale".

With or without boundary

Assuming a finite universe, the universe can either have an edge or no edge. Many finite mathematical spaces, e.g., a disc, have an edge or boundary. Spaces that have an edge are difficult to treat, both conceptually and mathematically. Namely, it is very difficult to state what would happen at the edge of such a universe. For this reason, spaces that have an edge are typically excluded from consideration.

However, there exist many finite spaces, such as the 3-sphere and 3-torus, which have no edges. Mathematically, these spaces are referred to as being compact without boundary. The term compact means that it is finite in extent ("bounded") and complete. The term "without boundary" means that the space has no edges. Moreover, so that calculus can be applied, the universe is typically assumed to be a differentiable manifold. A mathematical object that possesses all these properties, compact without boundary and differentiable, is termed a closed manifold. The 3-sphere and 3-torus are both closed manifolds.

Observational methods

In the 1990s and early 2000s, empirical methods for determining the global topology using measurements on scales that would show multiple imaging were proposed [7] and applied to cosmological observations. [8] [9]

In the 2000s and 2010s, it was shown that, since the universe is inhomogeneous as shown in the cosmic web of large-scale structure, acceleration effects measured on local scales in the patterns of the movements of galaxies should, in principle, reveal the global topology of the universe. [10] [11] [12]

Curvature

The curvature of the universe places constraints on the topology. If the spatial geometry is spherical, i.e., possess positive curvature, the topology is compact. For a flat (zero curvature) or a hyperbolic (negative curvature) spatial geometry, the topology can be either compact or infinite. [7] Many textbooks erroneously state that a flat or hyperbolic universe implies an infinite universe; however, the correct statement is that a flat universe that is also simply connected implies an infinite universe. [7] For example, Euclidean space is flat, simply connected, and infinite, but there are tori which are flat, multiply connected, finite, and compact (see flat torus).

In general, local to global theorems in Riemannian geometry relate the local geometry to the global geometry. If the local geometry has constant curvature, the global geometry is very constrained, as described in Thurston geometries.

The latest research shows that even the most powerful future experiments (like the SKA) will not be able to distinguish between flat, open and closed universe if the true value of cosmological curvature parameter is smaller than 10−4. If the true value of the cosmological curvature parameter is larger than 10−3 we will be able to distinguish between these three models even now. [13]

Final results of the Planck mission, released in 2018 show the cosmological curvature parameter, 1 − Ω = ΩK = −Kc2/a2H2, to be 0.0007±0.0019, consistent with a flat universe. [14] (i.e. positive curvature: K = +1, ΩK < 0, Ω > 1, negative curvature: K = −1, ΩK > 0, Ω < 1, zero curvature: K = 0, ΩK = 0, Ω = 1).

Universe with zero curvature

In a universe with zero curvature, the local geometry is flat. The most obvious global structure is that of Euclidean space, which is infinite in extent. Flat universes that are finite in extent include the torus and Klein bottle. Moreover, in three dimensions, there are 10 finite closed flat 3-manifolds, of which 6 are orientable and 4 are non-orientable. These are the Bieberbach manifolds. The most familiar is the aforementioned 3-torus universe.

In the absence of dark energy, a flat universe expands forever but at a continually decelerating rate, with expansion asymptotically approaching zero. With dark energy, the expansion rate of the universe initially slows down, due to the effect of gravity, but eventually increases. The ultimate fate of the universe is the same as that of an open universe in the sense that space will continue expanding forever.

A flat universe can have zero total energy. [15]

Universe with positive curvature

A positively curved universe is described by elliptic geometry, and can be thought of as a three-dimensional hypersphere, or some other spherical 3-manifold (such as the Poincaré dodecahedral space), all of which are quotients of the 3-sphere.

Poincaré dodecahedral space is a positively curved space, colloquially described as "soccerball-shaped", as it is the quotient of the 3-sphere by the binary icosahedral group, which is very close to icosahedral symmetry, the symmetry of a soccer ball. This was proposed by Jean-Pierre Luminet and colleagues in 2003 [8] [16] and an optimal orientation on the sky for the model was estimated in 2008. [9]

Universe with negative curvature

A hyperbolic universe, one of a negative spatial curvature, is described by hyperbolic geometry, and can be thought of locally as a three-dimensional analog of an infinitely extended saddle shape. There are a great variety of hyperbolic 3-manifolds, and their classification is not completely understood. Those of finite volume can be understood via the Mostow rigidity theorem. For hyperbolic local geometry, many of the possible three-dimensional spaces are informally called "horn topologies", so called because of the shape of the pseudosphere, a canonical model of hyperbolic geometry. An example is the Picard horn, a negatively curved space, colloquially described as "funnel-shaped". [17]

Curvature: open or closed

When cosmologists speak of the universe as being "open" or "closed", they most commonly are referring to whether the curvature is negative or positive, respectively. These meanings of open and closed are different from the mathematical meaning of open and closed used for sets in topological spaces and for the mathematical meaning of open and closed manifolds, which gives rise to ambiguity and confusion. In mathematics, there are definitions for a closed manifold (i.e., compact without boundary) and open manifold (i.e., one that is not compact and without boundary). A "closed universe" is necessarily a closed manifold. An "open universe" can be either a closed or open manifold. For example, in the Friedmann–Lemaître–Robertson–Walker (FLRW) model, the universe is considered to be without boundaries, in which case "compact universe" could describe a universe that is a closed manifold.

See also

Related Research Articles

<span class="mw-page-title-main">Surface (topology)</span> Two-dimensional manifold

In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

<span class="mw-page-title-main">Topology</span> Branch of mathematics

Topology is the part of mathematics concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself.

<span class="mw-page-title-main">Universe</span> Everything in space and time

The universe is all of space and time and their contents. It comprises all of existence, any fundamental interaction, physical process and physical constant, and therefore all forms of energy and matter, and the structures they form, from sub-atomic particles to entire galaxies. Space and time, according to the prevailing cosmological theory of the Big Bang, emerged together 13.787±0.020 billion years ago, and the universe has been expanding ever since. Today the universe has expanded into an age and size that is physically only in parts observable as the observable universe, which is approximately 93 billion light-years in diameter at the present day, while the spatial size, if any, of the entire universe is unknown.

<span class="mw-page-title-main">Calabi–Yau manifold</span> Riemannian manifold with SU(n) holonomy

In algebraic and differential geometry, a Calabi–Yau manifold, also known as a Calabi–Yau space, is a particular type of manifold which has properties, such as Ricci flatness, yielding applications in theoretical physics. Particularly in superstring theory, the extra dimensions of spacetime are sometimes conjectured to take the form of a 6-dimensional Calabi–Yau manifold, which led to the idea of mirror symmetry. Their name was coined by Candelas et al. (1985), after Eugenio Calabi who first conjectured that such surfaces might exist, and Shing-Tung Yau who proved the Calabi conjecture.

The ultimate fate of the universe is a topic in physical cosmology, whose theoretical restrictions allow possible scenarios for the evolution and ultimate fate of the universe to be described and evaluated. Based on available observational evidence, deciding the fate and evolution of the universe has become a valid cosmological question, being beyond the mostly untestable constraints of mythological or theological beliefs. Several possible futures have been predicted by different scientific hypotheses, including that the universe might have existed for a finite and infinite duration, or towards explaining the manner and circumstances of its beginning.

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.

In mathematics, Thurston's geometrization conjecture states that each of certain three-dimensional topological spaces has a unique geometric structure that can be associated with it. It is an analogue of the uniformization theorem for two-dimensional surfaces, which states that every simply connected Riemann surface can be given one of three geometries . In three dimensions, it is not always possible to assign a single geometry to a whole topological space. Instead, the geometrization conjecture states that every closed 3-manifold can be decomposed in a canonical way into pieces that each have one of eight types of geometric structure. The conjecture was proposed by William Thurston, and implies several other conjectures, such as the Poincaré conjecture and Thurston's elliptization conjecture.

<span class="mw-page-title-main">Ricci flow</span> Partial differential equation

In the mathematical fields of differential geometry and geometric analysis, the Ricci flow, sometimes also referred to as Hamilton's Ricci flow, is a certain partial differential equation for a Riemannian metric. It is often said to be analogous to the diffusion of heat and the heat equation, due to formal similarities in the mathematical structure of the equation. However, it is nonlinear and exhibits many phenomena not present in the study of the heat equation.

The Penrose–Hawking singularity theorems are a set of results in general relativity that attempt to answer the question of when gravitation produces singularities. The Penrose singularity theorem is a theorem in semi-Riemannian geometry and its general relativistic interpretation predicts a gravitational singularity in black hole formation. The Hawking singularity theorem is based on the Penrose theorem and it is interpreted as a gravitational singularity in the Big Bang situation. Penrose was awarded the Nobel Prize in Physics in 2020 "for the discovery that black hole formation is a robust prediction of the general theory of relativity", which he shared with Reinhard Genzel and Andrea Ghez.

<span class="mw-page-title-main">Homogeneous space</span> Topological space in group theory

In mathematics, a homogeneous space is, very informally, a space that looks the same everywhere, as you move through it, with movement given by the action of a group. Homogeneous spaces occur in the theories of Lie groups, algebraic groups and topological groups. More precisely, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts transitively. The elements of G are called the symmetries of X. A special case of this is when the group G in question is the automorphism group of the space X – here "automorphism group" can mean isometry group, diffeomorphism group, or homeomorphism group. In this case, X is homogeneous if intuitively X looks locally the same at each point, either in the sense of isometry, diffeomorphism, or homeomorphism (topology). Some authors insist that the action of G be faithful, although the present article does not. Thus there is a group action of G on X that can be thought of as preserving some "geometric structure" on X, and making X into a single G-orbit.

In mathematics and especially differential geometry, a Kähler manifold is a manifold with three mutually compatible structures: a complex structure, a Riemannian structure, and a symplectic structure. The concept was first studied by Jan Arnoldus Schouten and David van Dantzig in 1930, and then introduced by Erich Kähler in 1933. The terminology has been fixed by André Weil. Kähler geometry refers to the study of Kähler manifolds, their geometry and topology, as well as the study of structures and constructions that can be performed on Kähler manifolds, such as the existence of special connections like Hermitian Yang–Mills connections, or special metrics such as Kähler–Einstein metrics.

In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer . That is,

<span class="mw-page-title-main">Low-dimensional topology</span> Branch of topology

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.

<span class="mw-page-title-main">3-manifold</span> Mathematical space

In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.

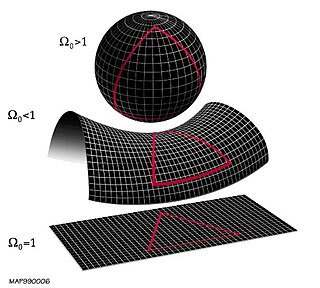
<span class="mw-page-title-main">Flatness problem</span> Cosmological fine-tuning problem

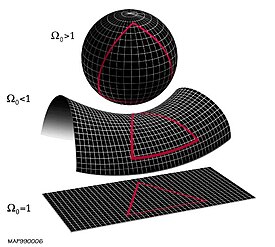
The flatness problem is a cosmological fine-tuning problem within the Big Bang model of the universe. Such problems arise from the observation that some of the initial conditions of the universe appear to be fine-tuned to very 'special' values, and that small deviations from these values would have extreme effects on the appearance of the universe at the current time.

In mathematics, more precisely in topology and differential geometry, a hyperbolic 3-manifold is a manifold of dimension 3 equipped with a hyperbolic metric, that is a Riemannian metric which has all its sectional curvatures equal to −1. It is generally required that this metric be also complete: in this case the manifold can be realised as a quotient of the 3-dimensional hyperbolic space by a discrete group of isometries.

The expansion of the universe is the increase in distance between gravitationally unbound parts of the observable universe with time. It is an intrinsic expansion, so it does not mean that the universe expands "into" anything or that space exists "outside" it. To any observer in the universe, it appears that all but the nearest galaxies recede at speeds that are proportional to their distance from the observer, on average. While objects cannot move faster than light, this limitation applies only with respect to local reference frames and does not limit the recession rates of cosmologically distant objects.

<span class="mw-page-title-main">Causal sets</span> Approach to quantum gravity using discrete spacetime

The causal sets program is an approach to quantum gravity. Its founding principles are that spacetime is fundamentally discrete and that spacetime events are related by a partial order. This partial order has the physical meaning of the causality relations between spacetime events.

In mathematics, spaces of non-positive curvature occur in many contexts and form a generalization of hyperbolic geometry. In the category of Riemannian manifolds, one can consider the sectional curvature of the manifold and require that this curvature be everywhere less than or equal to zero. The notion of curvature extends to the category of geodesic metric spaces, where one can use comparison triangles to quantify the curvature of a space; in this context, non-positively curved spaces are known as (locally) CAT(0) spaces.

In mathematics, the curve complex is a simplicial complex C(S) associated to a finite-type surface S, which encodes the combinatorics of simple closed curves on S. The curve complex turned out to be a fundamental tool in the study of the geometry of the Teichmüller space, of mapping class groups and of Kleinian groups. It was introduced by W.J.Harvey in 1978.

References

  1. ↑ "Will the Universe expand forever?". NASA. 24 January 2014. Retrieved 16 March 2015.
  2. ↑ Biron, Lauren (7 April 2015). "Our universe is Flat". symmetrymagazine.org. FermiLab/SLAC.
  3. ↑ "Density Parameter, Omega". hyperphysics.phy-astr.gsu.edu. Retrieved 2015-06-01.
  4. ↑ Ade, P. A. R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A. J.; Barreiro, R. B.; Bartlett, J. G.; Battaner, E.; Benabed, K.; Benoît, A.; Benoit-Lévy, A.; Bernard, J.-P.; Bersanelli, M.; Bielewicz, P.; Bobin, J.; Bock, J. J.; Bonaldi, A.; Bond, J. R.; Borrill, J.; Bouchet, F. R.; Bridges, M.; Bucher, M.; Burigana, C.; Butler, R. C.; Calabrese, E.; et al. (2014). "Planck2013 results. XVI. Cosmological parameters". Astronomy & Astrophysics. 571: A16. arXiv: 1303.5076 . Bibcode:2014A&A...571A..16P. doi:10.1051/0004-6361/201321591. S2CID   118349591.
  5. ↑ De Bernardis, P.; Ade, P. A. R.; Bock, J. J.; Bond, J. R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B. P.; De Gasperis, G.; Farese, P. C.; Ferreira, P. G.; Ganga, K.; Giacometti, M.; Hivon, E.; Hristov, V. V.; Iacoangeli, A.; Jaffe, A. H.; Lange, A. E.; Martinis, L.; Masi, S.; Mason, P. V.; Mauskopf, P. D.; Melchiorri, A.; Miglio, L.; Montroy, T.; Netterfield, C. B.; Pascale, E.; Piacentini, F.; Pogosyan, D.; et al. (2000). "A flat Universe from high-resolution maps of the cosmic microwave background radiation". Nature. 404 (6781): 955–9. arXiv: astro-ph/0004404 . Bibcode:2000Natur.404..955D. doi:10.1038/35010035. PMID   10801117. S2CID   4412370.
  6. ↑ Davies, P. C. W. (1977). Space and time in the modern universe. cambridge university press. ISBN   978-0-521-29151-4.
  7. 1 2 3 Luminet, Jean-Pierre; Lachièze-Rey, Marc (1995). "Cosmic Topology". Physics Reports. 254 (3): 135–214. arXiv: gr-qc/9605010 . Bibcode:1995PhR...254..135L. doi:10.1016/0370-1573(94)00085-h. S2CID   119500217.
  8. 1 2 Luminet, Jean-Pierre; Weeks, Jeff; Riazuelo, Alain; Lehoucq, Roland; Uzan, Jean-Phillipe (2003-10-09). "Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background". Nature . 425 (6958): 593–595. arXiv: astro-ph/0310253 . Bibcode:2003Natur.425..593L. doi:10.1038/nature01944. PMID   14534579. S2CID   4380713.
  9. 1 2 Roukema, Boudewijn; Buliński, Zbigniew; Szaniewska, Agnieszka; Gaudin, Nicolas E. (2008). "A test of the Poincare dodecahedral space topology hypothesis with the WMAP CMB data". Astronomy and Astrophysics. 482 (3): 747. arXiv: 0801.0006 . Bibcode:2008A&A...482..747L. doi:10.1051/0004-6361:20078777. S2CID   1616362.
  10. ↑ Boudewijn François Roukema; Bajtlik S.; Biesiada M.; Szaniewska A.; Jurkiewicz H. (2007). "A weak acceleration effect due to residual gravity in a multiply connected universe". Astronomy & Astrophysics . 463: 861–871. arXiv: astro-ph/0602159 . Bibcode:2007A&A...463..861R. doi:10.1051/0004-6361:20064979. ISSN   0004-6361. Zbl   1118.85330. Wikidata   Q68598777.
  11. ↑ Boudewijn François Roukema; Rozanski P. T. (2009). "The residual gravity acceleration effect in the Poincare dodecahedral space". Astronomy & Astrophysics . 502: 27–35. arXiv: 0902.3402 . Bibcode:2009A&A...502...27R. doi:10.1051/0004-6361/200911881. ISSN   0004-6361. Zbl   1177.85087. Wikidata   Q68676519.
  12. ↑ Jan J Ostrowski; Boudewijn F Roukema; Zbigniew P Buliński (30 July 2012). "A relativistic model of the topological acceleration effect". Classical and Quantum Gravity . 29 (16): 165006. arXiv: 1109.1596 . doi:10.1088/0264-9381/29/16/165006. ISSN   0264-9381. Zbl   1253.83052. Wikidata   Q96692451.
  13. ↑ Vardanyan, Mihran; Trotta, Roberto; Silk, Joseph (2009). "How flat can you get? A model comparison perspective on the curvature of the Universe". Monthly Notices of the Royal Astronomical Society. 397 (1): 431–444. arXiv: 0901.3354 . Bibcode:2009MNRAS.397..431V. doi:10.1111/j.1365-2966.2009.14938.x. S2CID   15995519.
  14. ↑ Planck Collaboration; Ade, P. A. R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A. J.; Barreiro, R. B.; Bartlett, J. G.; Bartolo, N.; Battaner, E.; Battye, R.; Benabed, K.; Benoit, A.; Benoit-Levy, A.; Bernard, J. P.; Bersanelli, M.; Bielewicz, P.; Bonaldi, A.; Bonavera, L.; Bond, J. R.; Borrill, J.; Bouchet, F. R.; Boulanger, F.; Bucher, M.; Burigana, C.; Butler, R. C.; Calabrese, E.; et al. (2020). "Planck 2018 results. VI. Cosmological parameters". Astronomy & Astrophysics. 641: A6. arXiv: 1807.06209 . Bibcode:2020A&A...641A...6P. doi:10.1051/0004-6361/201833910. S2CID   119335614.
  15. ↑ "A Universe From Nothing lecture by Lawrence Krauss at AAI". YouTube . 2009. Archived from the original on 2021-12-15. Retrieved 17 October 2011.
  16. ↑ "Is the universe a dodecahedron?", article at PhysicsWeb.
  17. ↑ Aurich, Ralf; Lustig, S.; Steiner, F.; Then, H. (2004). "Hyperbolic Universes with a Horned Topology and the CMB Anisotropy". Classical and Quantum Gravity . 21 (21): 4901–4926. arXiv: astro-ph/0403597 . Bibcode:2004CQGra..21.4901A. doi:10.1088/0264-9381/21/21/010. S2CID   17619026.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.