Dean number

Last updated May 23, 2024

The Dean number (De) is a dimensionless group in fluid mechanics, which occurs in the study of flow in curved pipes and channels. It is named after the British scientist W. R. Dean, who was the first to provide a theoretical solution of the fluid motion through curved pipes for laminar flow by using a perturbation procedure from a Poiseuille flow in a straight pipe to a flow in a pipe with very small curvature.^[1]^[2]

Physical Context

Schematic of a pair of Dean vortices that form in curved pipes. DeanVortices.svg — Schematic of a pair of Dean vortices that form in curved pipes.

If a fluid is moving along a straight pipe that after some point becomes curved, then the flow entering a curved portion develops a centrifugal force in an asymmetrical geometry ^[3]. Such asymmetricity affects the parabolic velocity profile and causes a shift in the location of the maximum velocity compared to a straight pipe. Therefore, the maximum velocity shifts from the centerline towards the concave outer wall and forms an asymmetric velocity profile. There will be an adverse pressure gradient generated from the curvature with an increase in pressure, therefore a decrease in velocity close to the convex wall, and the contrary occurring towards the concave outer wall of the pipe. This gives rise to a secondary motion superposed on the primary flow, with the fluid in the centre of the pipe being swept towards the outer side of the bend and the fluid near the pipe wall will return towards the inside of the bend. This secondary motion is expected to appear as a pair of counter-rotating cells, which are called Dean vortices.

Definition

The Dean number is typically denoted by De (or Dn). For a flow in a pipe or tube it is defined as:

{\mathit {De}}={\frac {\sqrt {{\frac {1}{2}}\,({\text{inertial forces}})({\text{centrifugal forces}})}}{\text{viscous forces}}}={\frac {\sqrt {{\frac {1}{2}}\,(\rho \,D^{2}\,R_{c}\,{\frac {v^{2}}{D}})(\rho \,D^{2}\,R_{c}\,{\frac {v^{2}}{R_{c}}})}}{\mu {\frac {v}{D}}D\,R_{c}}}={\frac {\rho \,D\,v}{\mu }}{\sqrt {\frac {D}{2\,R_{c}}}}={\textit {Re}}\,{\sqrt {\frac {D}{2\,R_{c}}}}

where

$\rho$ is the density of the fluid
$\mu$ is the dynamic viscosity
$v$ is the axial velocity scale
$D$ is the diameter (for non-circular geometry, an equivalent diameter is used; see Reynolds number)
$R_{c}$ is the radius of curvature of the path of the channel.
${\textit {Re}}$ is the Reynolds number.

The Dean number is therefore the product of the Reynolds number (based on axial flow $v$ through a pipe of diameter $D$ ) and the square root of the curvature ratio.

Turbulence transition

The flow is completely unidirectional for low Dean numbers (De < 40~60). As the Dean number increases between 40~60 to 64~75, some wavy perturbations can be observed in the cross-section, which evidences some secondary flow. At higher Dean numbers than that (De > 64~75) the pair of Dean vortices becomes stable, indicating a primary dynamic instability. A secondary instability appears for De > 75~200, where the vortices present undulations, twisting, and eventually merging and pair splitting. Fully turbulent flow forms for De > 400.^[4] Transition from laminar to turbulent flow has also been examined in a number of studies, even though no universal solution exists since the parameter is highly dependent on the curvature ratio.^[5] Somewhat unexpectedly, laminar flow can be maintained for larger Reynolds numbers (even by a factor of two for the highest curvature ratios studied) than for straight pipes, even though curvature is known to cause instability.^[6]

The Dean equations

The Dean number appears in the so-called Dean equations.^[7] These are an approximation to the full Navier–Stokes equations for the steady axially uniform flow of a Newtonian fluid in a toroidal pipe, obtained by retaining just the leading order curvature effects (i.e. the leading-order equations for $a/r\ll 1$ ).

We use orthogonal coordinates $(x,y,z)$ with corresponding unit vectors $({\hat {\boldsymbol {x}}},{\hat {\boldsymbol {y}}},{\hat {\boldsymbol {z}}})$ aligned with the centre-line of the pipe at each point. The axial direction is ${\hat {\boldsymbol {z}}}$ , with ${\hat {\boldsymbol {x}}}$ being the normal in the plane of the centre-line, and ${\hat {\boldsymbol {y}}}$ the binormal. For an axial flow driven by a pressure gradient $G$ , the axial velocity $u_{z}$ is scaled with $U=Ga^{2}/\mu$ . The cross-stream velocities $u_{x},u_{y}$ are scaled with $(a/R)^{1/2}U$ , and cross-stream pressures with $\rho aU^{2}/L$ . Lengths are scaled with the tube radius $a$ .

In terms of these non-dimensional variables and coordinates, the Dean equations are then

De\left({\frac {\mathrm {D} u_{x}}{\mathrm {D} t}}-u_{z}^{2}\right)=-De{\frac {\partial p}{\partial x}}+\nabla ^{2}u_{x}

De{\frac {\mathrm {D} u_{y}}{\mathrm {D} t}}=-De{\frac {\partial p}{\partial y}}+\nabla ^{2}u_{y}

De{\frac {\mathrm {D} u_{z}}{\mathrm {D} t}}=1+\nabla ^{2}u_{z}

{\frac {\partial u_{x}}{\partial x}}+{\frac {\partial u_{y}}{\partial y}}=0

where

{\frac {\mathrm {D} }{\mathrm {D} t}}=u_{x}{\frac {\partial }{\partial x}}+u_{y}{\frac {\partial }{\partial y}}

is the convective derivative.

The Dean number De is the only parameter left in the system, and encapsulates the leading order curvature effects. Higher-order approximations will involve additional parameters.

For weak curvature effects (small De), the Dean equations can be solved as a series expansion in De. The first correction to the leading-order axial Poiseuille flow is a pair of vortices in the cross-section carrying flow from the inside to the outside of the bend across the centre and back around the edges. This solution is stable up to a critical Dean number $De_{c}\approx 956$ .^[8] For larger De, there are multiple solutions, many of which are unstable.

Related Research Articles

A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.

<span class="mw-page-title-main">Navier–Stokes equations</span> Equations describing the motion of viscous fluid substances

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In fluid mechanics, the Grashof number is a dimensionless number which approximates the ratio of the buoyancy to viscous forces acting on a fluid. It frequently arises in the study of situations involving natural convection and is analogous to the Reynolds number.

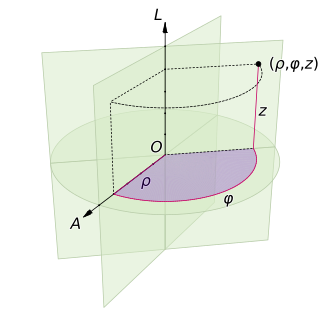
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis (axis L in the image opposite), the direction from the axis relative to a chosen reference direction (axis A), and the distance from a chosen reference plane perpendicular to the axis (plane containing the purple section). The latter distance is given as a positive or negative number depending on which side of the reference plane faces the point.

In fluid dynamics, two types of stream function are defined:

In fluid dynamics, the Euler equations are a set of

Fluid statics or hydrostatics is the branch of fluid mechanics that studies fluids at hydrostatic equilibrium and "the pressure in a fluid or exerted by a fluid on an immersed body".

The Weber number (We) is a dimensionless number in fluid mechanics that is often useful in analysing fluid flows where there is an interface between two different fluids, especially for multiphase flows with strongly curved surfaces. It is named after Moritz Weber (1871–1951). It can be thought of as a measure of the relative importance of the fluid's inertia compared to its surface tension. The quantity is useful in analyzing thin film flows and the formation of droplets and bubbles.

Stokes flow, also named creeping flow or creeping motion, is a type of fluid flow where advective inertial forces are small compared with viscous forces. The Reynolds number is low, i.e. $. This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small. Creeping flow was first studied to understand lubrication. In nature, this type of flow occurs in the swimming of microorganisms and sperm. In technology, it occurs in paint, MEMS devices, and in the flow of viscous polymers generally.$

The Navier–Stokes existence and smoothness problem concerns the mathematical properties of solutions to the Navier–Stokes equations, a system of partial differential equations that describe the motion of a fluid in space. Solutions to the Navier–Stokes equations are used in many practical applications. However, theoretical understanding of the solutions to these equations is incomplete. In particular, solutions of the Navier–Stokes equations often include turbulence, which remains one of the greatest unsolved problems in physics, despite its immense importance in science and engineering.

The shallow-water equations (SWE) are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid. The shallow-water equations in unidirectional form are also called Saint-Venant equations, after Adhémar Jean Claude Barré de Saint-Venant.

The derivation of the Navier–Stokes equations as well as their application and formulation for different families of fluids, is an important exercise in fluid dynamics with applications in mechanical engineering, physics, chemistry, heat transfer, and electrical engineering. A proof explaining the properties and bounds of the equations, such as Navier–Stokes existence and smoothness, is one of the important unsolved problems in mathematics.

The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.

In nonideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Hagen in 1839 and then by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845.

In fluid dynamics, the Stokes stream function is used to describe the streamlines and flow velocity in a three-dimensional incompressible flow with axisymmetry. A surface with a constant value of the Stokes stream function encloses a streamtube, everywhere tangential to the flow velocity vectors. Further, the volume flux within this streamtube is constant, and all the streamlines of the flow are located on this surface. The velocity field associated with the Stokes stream function is solenoidal—it has zero divergence. This stream function is named in honor of George Gabriel Stokes.

In fluid dynamics, Luke's variational principle is a Lagrangian variational description of the motion of surface waves on a fluid with a free surface, under the action of gravity. This principle is named after J.C. Luke, who published it in 1967. This variational principle is for incompressible and inviscid potential flows, and is used to derive approximate wave models like the mild-slope equation, or using the averaged Lagrangian approach for wave propagation in inhomogeneous media.

In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.

In fluid dynamics, the radiation stress is the depth-integrated – and thereafter phase-averaged – excess momentum flux caused by the presence of the surface gravity waves, which is exerted on the mean flow. The radiation stresses behave as a second-order tensor.

Blade element momentum theory is a theory that combines both blade element theory and momentum theory. It is used to calculate the local forces on a propeller or wind-turbine blade. Blade element theory is combined with momentum theory to alleviate some of the difficulties in calculating the induced velocities at the rotor.

In fluid dynamics, Hicks equation, sometimes also referred as Bragg–Hawthorne equation or Squire–Long equation, is a partial differential equation that describes the distribution of stream function for axisymmetric inviscid fluid, named after William Mitchinson Hicks, who derived it first in 1898. The equation was also re-derived by Stephen Bragg and William Hawthorne in 1950 and by Robert R. Long in 1953 and by Herbert Squire in 1956. The Hicks equation without swirl was first introduced by George Gabriel Stokes in 1842. The Grad–Shafranov equation appearing in plasma physics also takes the same form as the Hicks equation.

References

↑ Dean, W. R. (1927). "Note on the motion of fluid in a curved pipe". Phil. Mag. 4 (20): 208–223. doi:10.1080/14786440708564324.
↑ Dean, W. R. (1928). "The streamline motion of fluid in a curved pipe". Phil. Mag. Series 7. 5 (30): 673–695. doi:10.1080/14786440408564513.
↑ https://www.mdpi.com/2072-666X/14/12/2202
↑ Ligrani, Phillip M. "A Study of Dean Vortex Development and Structure in a Curved Rectangular Channel With Aspect Ratio of 40 at Dean Numbers up to 430", U.S. Army Research Laboratory (Contractor Report ARL-CR-l44) and Lewis Research Center (NASA Contractor Report 4607), July 1994. Retrieved on 11 July 2017.
↑ Kalpakli, Athanasia (2012). Experimental study of turbulent flows through pipe bends (Thesis). Stockholm, Sweden: Royal Institute of Technology KTH Mechanics. pp. 461–512.
↑ Taylor, G. I. (1929). "The criterion for turbulence in curved pipes". Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 124 (794): 243–249. Bibcode:1929RSPSA.124..243T. doi: 10.1098/rspa.1929.0111 .
↑ Mestel, J. Flow in curved pipes: The Dean equations, Lecture Handout for Course M4A33, Imperial College.
↑ Dennis, C. R.; Ng, M. (1982). "Dual solutions for steady laminar-flow through a curved tube". Q. J. Mech. Appl. Math. 35 (3): 305. doi:10.1093/qjmam/35.3.305.