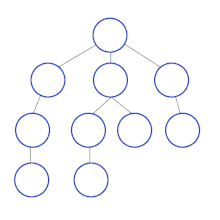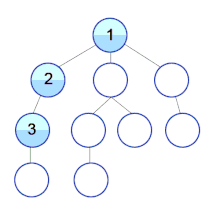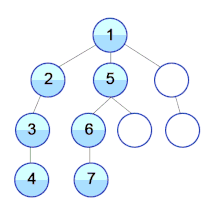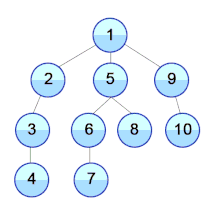
Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. It starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next depth level. Extra memory, usually a queue, is needed to keep track of the child nodes that were encountered but not yet explored.
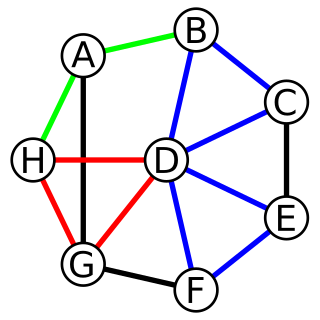
In graph theory, a cycle in a graph is a non-empty trail in which only the first and last vertices are equal. A directed cycle in a directed graph is a non-empty directed trail in which only the first and last vertices are equal.
In computer science, iterative deepening search or more specifically iterative deepening depth-first search is a state space/graph search strategy in which a depth-limited version of depth-first search is run repeatedly with increasing depth limits until the goal is found. IDDFS is optimal, meaning that it finds the shallowest goal. Since it visits all the nodes in the search tree down to depth before visiting any nodes at depth , the cumulative order in which nodes are first visited is effectively the same as in breadth-first search. However, IDDFS uses much less memory.
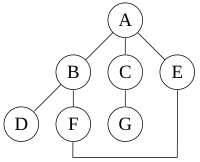
In computer science, tree traversal is a form of graph traversal and refers to the process of visiting each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well.

In the mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of an arbitrary directed graph form a partition into subgraphs that are themselves strongly connected. It is possible to test the strong connectivity of a graph, or to find its strongly connected components, in linear time (that is, Θ(V + E)).
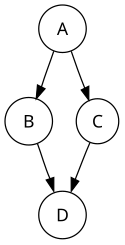
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge (u,v) from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is possible even when the DAG has disconnected components.
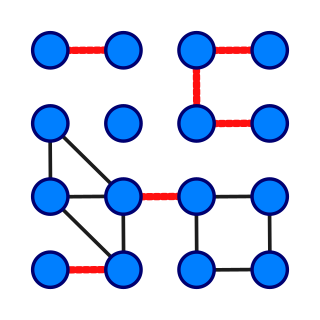
In graph theory, a bridge, isthmus, cut-edge, or cut arc is an edge of a graph whose deletion increases the graph's number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle. For a connected graph, a bridge can uniquely determine a cut. A graph is said to be bridgeless or isthmus-free if it contains no bridges.
In computer science, Kosaraju-Sharir's algorithm is a linear time algorithm to find the strongly connected components of a directed graph. Aho, Hopcroft and Ullman credit it to S. Rao Kosaraju and Micha Sharir. Kosaraju suggested it in 1978 but did not publish it, while Sharir independently discovered it and published it in 1981. It makes use of the fact that the transpose graph has exactly the same strongly connected components as the original graph.

In graph theory, a biconnected component is a maximal biconnected subgraph. Any connected graph decomposes into a tree of biconnected components called the block-cut tree of the graph. The blocks are attached to each other at shared vertices called cut vertices or separating vertices or articulation points. Specifically, a cut vertex is any vertex whose removal increases the number of connected components.
In computer science, the Hopcroft–Karp algorithm is an algorithm that takes a bipartite graph as input and produces a maximum-cardinality matching as output — a set of as many edges as possible with the property that no two edges share an endpoint. It runs in time in the worst case, where is set of edges in the graph, is set of vertices of the graph, and it is assumed that . In the case of dense graphs the time bound becomes , and for sparse random graphs it runs in time with high probability.
In computer science, graph traversal refers to the process of visiting each vertex in a graph. Such traversals are classified by the order in which the vertices are visited. Tree traversal is a special case of graph traversal.

Tarjan's strongly connected components algorithm is an algorithm in graph theory for finding the strongly connected components (SCCs) of a directed graph. It runs in linear time, matching the time bound for alternative methods including Kosaraju's algorithm and the path-based strong component algorithm. The algorithm is named for its inventor, Robert Tarjan.
In graph theory, the strongly connected components of a directed graph may be found using an algorithm that uses depth-first search in combination with two stacks, one to keep track of the vertices in the current component and the second to keep track of the current search path. Versions of this algorithm have been proposed by Purdom (1970), Munro (1971), Dijkstra (1976), Cheriyan & Mehlhorn (1996), and Gabow (2000); of these, Dijkstra's version was the first to achieve linear time.
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of vertices from an n-vertex graph can partition the graph into disjoint subgraphs each of which has at most vertices.
In graph theory, a Trémaux tree of an undirected graph is a type of spanning tree, generalizing depth-first search trees. They are defined by the property that every edge of connects an ancestor–descendant pair in the tree. Trémaux trees are named after Charles Pierre Trémaux, a 19th-century French author who used a form of depth-first search as a strategy for solving mazes. They have also been called normal spanning trees, especially in the context of infinite graphs.
In graph theory, a bipolar orientation or st-orientation of an undirected graph is an assignment of a direction to each edge that causes the graph to become a directed acyclic graph with a single source s and a single sink t, and an st-numbering of the graph is a topological ordering of the resulting directed acyclic graph.
External memory graph traversal is a type of graph traversal optimized for accessing externally stored memory.
Reverse-search algorithms are a class of algorithms for generating all objects of a given size, from certain classes of combinatorial objects. In many cases, these methods allow the objects to be generated in polynomial time per object, using only enough memory to store a constant number of objects. They work by organizing the objects to be generated into a spanning tree of their state space, and then performing a depth-first search of this tree.