In mathematics, a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. For example, the series
In mathematics, a series is, roughly speaking, the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance.
In mathematical analysis, Cesàro summation assigns values to some infinite sums that are not necessarily convergent in the usual sense. The Cesàro sum is defined as the limit, as n tends to infinity, of the sequence of arithmetic means of the first n partial sums of the series.
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a finite limit.
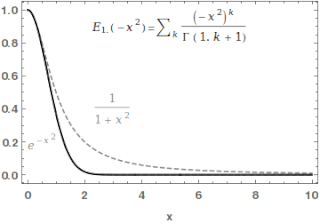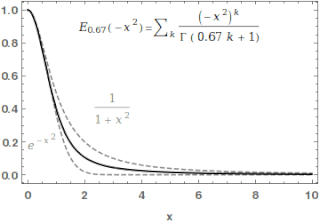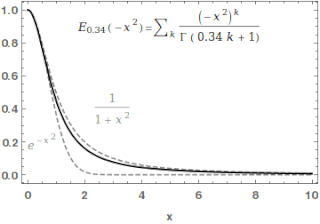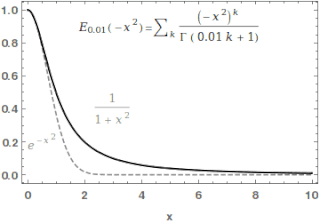
In mathematics, the Mittag-Leffler function is a special function, a complex function which depends on two complex parameters and . It may be defined by the following series when the real part of is strictly positive:
In mathematics, Borel summation is a summation method for divergent series, introduced by Émile Borel. It is particularly useful for summing divergent asymptotic series, and in some sense gives the best possible sum for such series. There are several variations of this method that are also called Borel summation, and a generalization of it called Mittag-Leffler summation.
In mathematics, in the area of complex analysis, Nachbin's theorem is commonly used to establish a bound on the growth rates for an analytic function. This article provides a brief review of growth rates, including the idea of a function of exponential type. Classification of growth rates based on type help provide a finer tool than big O or Landau notation, since a number of theorems about the analytic structure of the bounded function and its integral transforms can be stated. In particular, Nachbin's theorem may be used to give the domain of convergence of the generalized Borel transform, given below.
In mathematics, the infinite series 1 − 1 + 1 − 1 + ⋯, also written

This article lists occurrences of the paradoxical infinite "sum" +1 -1 +1 -1 ..., sometimes called Grandi's series.
Ramanujan summation is a technique invented by the mathematician Srinivasa Ramanujan for assigning a value to divergent infinite series. Although the Ramanujan summation of a divergent series is not a sum in the traditional sense, it has properties that make it mathematically useful in the study of divergent infinite series, for which conventional summation is undefined.
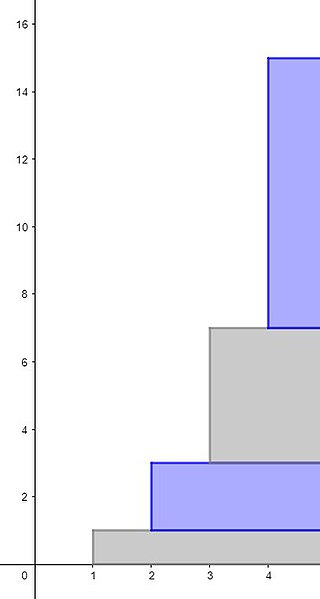
In mathematics, 1 + 2 + 4 + 8 + ⋯ is the infinite series whose terms are the successive powers of two. As a geometric series, it is characterized by its first term, 1, and its common ratio, 2. As a series of real numbers it diverges to infinity, so the sum of this series is infinity.

In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as

The infinite series whose terms are the natural numbers 1 + 2 + 3 + 4 + ⋯ is a divergent series. The nth partial sum of the series is the triangular number
In the mathematics of convergent and divergent series, Euler summation is a summation method. That is, it is a method for assigning a value to a series, different from the conventional method of taking limits of partial sums. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series. As well as being used to define values for divergent series, Euler summation can be used to speed the convergence of series.
In mathematics, 1 − 2 + 4 − 8 + ⋯ is the infinite series whose terms are the successive powers of two with alternating signs. As a geometric series, it is characterized by its first term, 1, and its common ratio, −2.

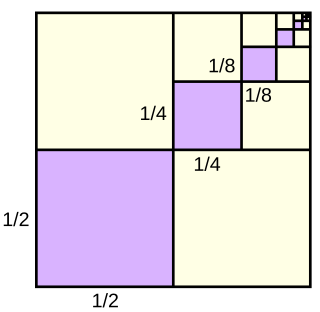
In mathematics, the infinite series 1/2 − 1/4 + 1/8 − 1/16 + ⋯ is a simple example of an alternating series that converges absolutely.
In mathematics, Mittag-Leffler summation is any of several variations of the Borel summation method for summing possibly divergent formal power series, introduced by Mittag-Leffler
The Mittag-Leffler distributions are two families of probability distributions on the half-line . They are parametrized by a real or . Both are defined with the Mittag-Leffler function, named after Gösta Mittag-Leffler.









