
In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies of an n-sided polygon, connected by an alternating band of 2n triangles. They are represented by the Conway notation An.

Martin Gardner was an American popular mathematics and popular science writer with interests also encompassing magic, scientific skepticism, micromagic, philosophy, religion, and literature – especially the writings of Lewis Carroll, L. Frank Baum, and G. K. Chesterton. He was a leading authority on Lewis Carroll; The Annotated Alice, which incorporated the text of Carroll's two Alice books, was his most successful work and sold over a million copies. He had a lifelong interest in magic and illusion and in 1999, MAGIC magazine named him as one of the "100 Most Influential Magicians of the Twentieth Century". He was considered the doyen of American puzzlers. He was a prolific and versatile author, publishing more than 100 books.

In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Möbius strip.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

Modular origami or unit origami is a two-stage paper folding technique in which several, or sometimes many, sheets of paper are first folded into individual modules or units and then assembled into an integrated flat shape or three-dimensional structure, usually by inserting flaps into pockets created by the folding process. These insertions create tension or friction that holds the model together.

In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids.

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.
A Heronian tetrahedron is a tetrahedron whose edge lengths, face areas and volume are all integers. The faces must therefore all be Heronian triangles . Every Heronian tetrahedron can be arranged in Euclidean space so that its vertex coordinates are also integers.

In geometry, a deltahedron is a polyhedron whose faces are all (congruent) equilateral triangles. The name is taken from the Greek upper case delta letter (Δ), which has the shape of an equilateral triangle. There are infinitely many deltahedra. By the handshaking lemma, each deltahedron has an even number of faces. Only eight deltahedra are strictly convex; these have 4, 6, 8, 10, 12, 14, 16, and 20 faces. These eight deltahedra, with their respective numbers of faces, edges, and vertices, are listed below.

In recreational mathematics, a polyhex is a polyform with a regular hexagon as the base form, constructed by joining together 1 or more hexagons. Specific forms are named by their number of hexagons: monohex, dihex, trihex, tetrahex, etc. They were named by David Klarner who investigated them.

In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid, with 60 isosceles triangle faces. Its dual is the truncated dodecahedron. It has also been called the kisicosahedron. It was first depicted, in a non-convex form with equilateral triangle faces, by Leonardo da Vinci in Luca Pacioli's Divina proportione, where it was named the icosahedron elevatum. The capsid of the Hepatitis A virus has the shape of a triakis icosahedron.

In geometry, a square pyramid is a pyramid with a square base, having a total of five faces. If the apex of the pyramid is directly above the center of the square, it is a right square pyramid with four isosceles triangles; otherwise, it is an oblique square pyramid. When all of the pyramid's edges are equal in length, its triangles are all equilateral, and it is called an equilateral square pyramid.

In geometry, the elongated triangular pyramid is one of the Johnson solids. As the name suggests, it can be constructed by elongating a tetrahedron by attaching a triangular prism to its base. Like any elongated pyramid, the resulting solid is topologically self-dual.

In geometry, the elongated square bipyramid is the polyhedron constructed by attaching two equilateral square pyramids onto a cube's faces that are opposite each other. It can also be seen as 4 lunes linked together with squares to squares and triangles to triangles. It is also been named the pencil cube or 12-faced pencil cube due to its shape.

In geometry, a spidron is a continuous flat geometric figure composed entirely of triangles, where, for every pair of joining triangles, each has a leg of the other as one of its legs, and neither has any point inside the interior of the other. A deformed spidron is a three-dimensional figure sharing the other properties of a specific spidron, as if that spidron were drawn on paper, cut out in a single piece, and folded along a number of legs.

In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.

In geometry, a disphenoid is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same shape are isotetrahedron, sphenoid, bisphenoid, isosceles tetrahedron, equifacial tetrahedron, almost regular tetrahedron, and tetramonohedron.

In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of Scientific American. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in Mathematics Magazine.
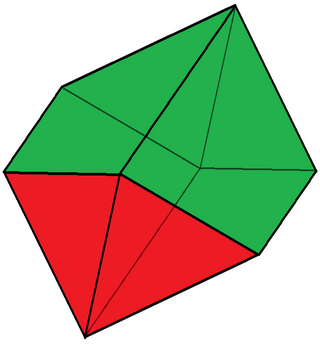
In geometry, an elongated octahedron is a polyhedron with 8 faces, 14 edges, and 8 vertices.

A kaleidocycle or flextangle is a flexible polyhedron connecting six tetrahedra on opposite edges into a cycle. If the faces of the disphenoids are equilateral triangles, it can be constructed from a stretched triangular tiling net with four triangles in one direction and an even number in the other direction.


























