In mathematics, the factorial of a non-negative integer , denoted by , is the product of all positive integers less than or equal to . The factorial of also equals the product of with the next smaller factorial:
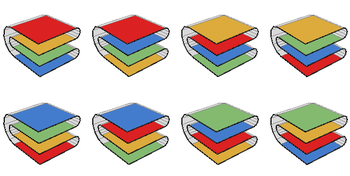
In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

The discipline of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability, and the use of paper folds to solve up-to cubic mathematical equations.

In geometry, a net of a polyhedron is an arrangement of non-overlapping edge-joined polygons in the plane which can be folded to become the faces of the polyhedron. Polyhedral nets are a useful aid to the study of polyhedra and solid geometry in general, as they allow for physical models of polyhedra to be constructed from material such as thin cardboard.
353 is the natural number following 352 and preceding 354. It is a prime number.
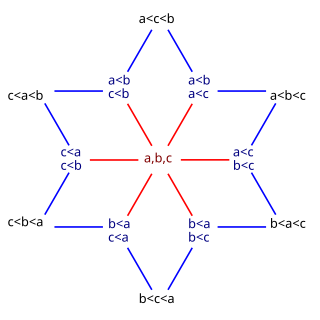
In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the number of weak orderings on a set of elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race). Starting from , these numbers are
Mousetrap is the name of a game introduced by the English mathematician Arthur Cayley. In the game, cards numbered through are shuffled to place them in some random permutation and are arranged in a circle with their faces up. Then, starting with the first card, the player begins counting and moving to the next card as the count is incremented. If at any point the player's current count matches the number on the card currently being pointed to, that card is removed from the circle and the player starts all over at on the next card. If the player ever removes all of the cards from the permutation in this manner, then the player wins. If the player reaches the count and cards still remain, then the game is lost.
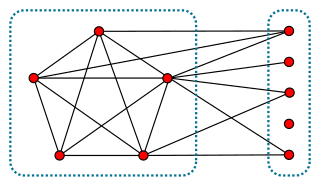
In graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set. Split graphs were first studied by Földes and Hammer, and independently introduced by Tyshkevich and Chernyak (1979).
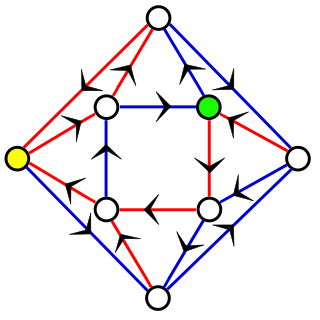
In computer science, more precisely, in the theory of deterministic finite automata (DFA), a synchronizing word or reset sequence is a word in the input alphabet of the DFA that sends any state of the DFA to one and the same state. That is, if an ensemble of copies of the DFA are each started in different states, and all of the copies process the synchronizing word, they will all end up in the same state. Not every DFA has a synchronizing word; for instance, a DFA with two states, one for words of even length and one for words of odd length, can never be synchronized.
In combinatorial mathematics and theoretical computer science, a permutation pattern is a sub-permutation of a longer permutation. Any permutation may be written in one-line notation as a sequence of digits representing the result of applying the permutation to the digit sequence 123...; for instance the digit sequence 213 represents the permutation on three elements that swaps elements 1 and 2. If π and σ are two permutations represented in this way, then π is said to contain σ as a pattern if some subsequence of the digits of π has the same relative order as all of the digits of σ.
In combinatorial mathematics, a partial permutation, or sequence without repetition, on a finite set S is a bijection between two specified subsets of S. That is, it is defined by two subsets U and V of equal size, and a one-to-one mapping from U to V. Equivalently, it is a partial function on S that can be extended to a permutation.

In combinatorics, the Schröder–Hipparchus numbers form an integer sequence that can be used to count the number of plane trees with a given set of leaves, the number of ways of inserting parentheses into a sequence, and the number of ways of dissecting a convex polygon into smaller polygons by inserting diagonals. These numbers begin

In mathematics, the telephone numbers or the involution numbers form a sequence of integers that count the ways n people can be connected by person-to-person telephone calls. These numbers also describe the number of matchings of a complete graph on n vertices, the number of permutations on n elements that are involutions, the sum of absolute values of coefficients of the Hermite polynomials, the number of standard Young tableaux with n cells, and the sum of the degrees of the irreducible representations of the symmetric group. Involution numbers were first studied in 1800 by Heinrich August Rothe, who gave a recurrence equation by which they may be calculated, giving the values
Anna Lubiw is a computer scientist known for her work in computational geometry and graph theory. She is currently a professor at the University of Waterloo.
The graph realization problem is a decision problem in graph theory. Given a finite sequence of natural numbers, the problem asks whether there is a labeled simple graph such that is the degree sequence of this graph.
In mathematics, a square-difference-free set is a set of natural numbers, no two of which differ by a square number. Hillel Furstenberg and András Sárközy proved in the late 1970s the Furstenberg–Sárközy theorem of additive number theory showing that, in a certain sense, these sets cannot be very large. In the game of subtract a square, the positions where the next player loses form a square-difference-free set. Another square-difference-free set is obtained by doubling the Moser–de Bruijn sequence.
In mathematics and computer science, the sorting numbers are a sequence of numbers introduced in 1950 by Hugo Steinhaus for the analysis of comparison sort algorithms. These numbers give the worst-case number of comparisons used by both binary insertion sort and merge sort. However, there are other algorithms that use fewer comparisons.
In the mathematics of paper folding, the big-little-big lemma is a necessary condition for a crease pattern with specified mountain folds and valley folds to be able to be folded flat. It differs from Kawasaki's theorem, which characterizes the flat-foldable crease patterns in which a mountain-valley assignment has not yet been made. Together with Maekawa's theorem on the total number of folds of each type, the big-little-big lemma is one of the two main conditions used to characterize the flat-foldability of mountain-valley assignments for crease patterns that meet the conditions of Kawasaki's theorem. Mathematical origami expert Tom Hull calls the big-little-big lemma "one of the most basic rules" for flat foldability of crease patterns.
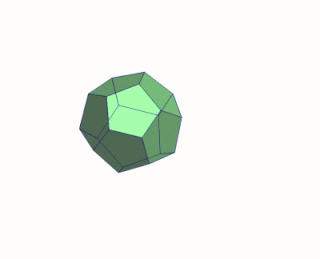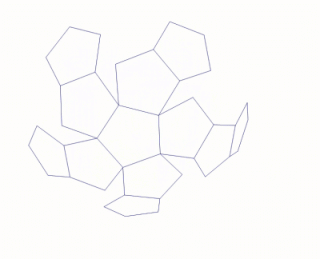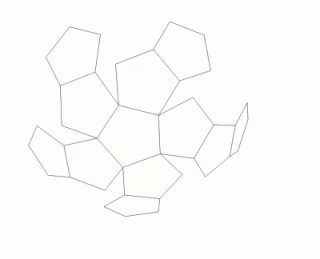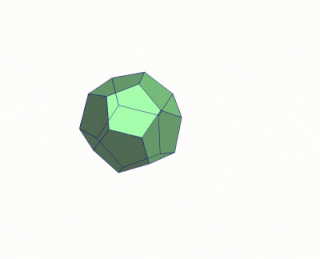
In the geometry of convex polyhedra, blooming or continuous blooming is a continuous three-dimensional motion of the surface of the polyhedron, cut to form a polyhedral net, from the polyhedron into a flat and non-self-overlapping placement of the net in a plane. As in rigid origami, the polygons of the net must remain individually flat throughout the motion, and are not allowed to intersect or cross through each other. A blooming, reversed to go from the flat net to a polyhedron, can be thought of intuitively as a way to fold the polyhedron from a paper net without bending the paper except at its designated creases.