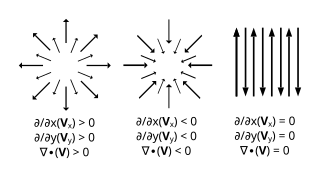
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference.
Ray transfer matrix analysis is a mathematical form for performing ray tracing calculations in sufficiently simple problems which can be solved considering only paraxial rays. Each optical element is described by a 2×2 ray transfer matrix which operates on a vector describing an incoming light ray to calculate the outgoing ray. Multiplication of the successive matrices thus yields a concise ray transfer matrix describing the entire optical system. The same mathematics is also used in accelerator physics to track particles through the magnet installations of a particle accelerator, see electron optics.
In vector calculus, the Jacobian matrix of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. When this matrix is square, that is, when the function takes the same number of variables as input as the number of vector components of its output, its determinant is referred to as the Jacobian determinant. Both the matrix and the determinant are often referred to simply as the Jacobian in literature.
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form
In mathematics, the Hessian matrix, Hessian or Hesse matrix is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named after him. Hesse originally used the term "functional determinants". The Hessian is sometimes denoted by H or, ambiguously, by ∇2.

In statistics, originally in geostatistics, kriging or Kriging, also known as Gaussian process regression, is a method of interpolation based on Gaussian process governed by prior covariances. Under suitable assumptions of the prior, kriging gives the best linear unbiased prediction (BLUP) at unsampled locations. Interpolating methods based on other criteria such as smoothness may not yield the BLUP. The method is widely used in the domain of spatial analysis and computer experiments. The technique is also known as Wiener–Kolmogorov prediction, after Norbert Wiener and Andrey Kolmogorov.
In mathematics and statistics, the quasi-arithmetic mean or generalised f-mean or Kolmogorov-Nagumo-de Finetti mean is one generalisation of the more familiar means such as the arithmetic mean and the geometric mean, using a function . It is also called Kolmogorov mean after Soviet mathematician Andrey Kolmogorov. It is a broader generalization than the regular generalized mean.

In the mathematical field of differential topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle. Technically, Hopf found a many-to-one continuous function from the 3-sphere onto the 2-sphere such that each distinct point of the 2-sphere is mapped from a distinct great circle of the 3-sphere. Thus the 3-sphere is composed of fibers, where each fiber is a circle — one for each point of the 2-sphere.
In multivariable calculus, the implicit function theorem is a tool that allows relations to be converted to functions of several real variables. It does so by representing the relation as the graph of a function. There may not be a single function whose graph can represent the entire relation, but there may be such a function on a restriction of the domain of the relation. The implicit function theorem gives a sufficient condition to ensure that there is such a function.
In signal processing, independent component analysis (ICA) is a computational method for separating a multivariate signal into additive subcomponents. This is done by assuming that at most one subcomponent is Gaussian and that the subcomponents are statistically independent from each other. ICA was invented by Jeanny Hérault and Christian Jutten in 1985. ICA is a special case of blind source separation. A common example application of ICA is the "cocktail party problem" of listening in on one person's speech in a noisy room.
In mathematical statistics, the Fisher information is a way of measuring the amount of information that an observable random variable X carries about an unknown parameter θ of a distribution that models X. Formally, it is the variance of the score, or the expected value of the observed information.
In statistics, econometrics, and signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it is used to describe certain time-varying processes in nature, economics, behavior, etc. The autoregressive model specifies that the output variable depends linearly on its own previous values and on a stochastic term ; thus the model is in the form of a stochastic difference equation which should not be confused with a differential equation. Together with the moving-average (MA) model, it is a special case and key component of the more general autoregressive–moving-average (ARMA) and autoregressive integrated moving average (ARIMA) models of time series, which have a more complicated stochastic structure; it is also a special case of the vector autoregressive model (VAR), which consists of a system of more than one interlocking stochastic difference equation in more than one evolving random variable.
An autoencoder is a type of artificial neural network used to learn efficient codings of unlabeled data. An autoencoder learns two functions: an encoding function that transforms the input data, and a decoding function that recreates the input data from the encoded representation. The autoencoder learns an efficient representation (encoding) for a set of data, typically for dimensionality reduction.
In machine learning, the vanishing gradient problem is encountered when training recurrent neural networks with gradient-based learning methods and backpropagation. In such methods, during each iteration of training each of the neural networks weights receives an update proportional to the partial derivative of the error function with respect to the current weight. The problem is that as the sequence length increases, the gradient magnitude typically is expected to decrease, slowing the training process. In the worst case, this may completely stop the neural network from further training. As one example of the problem cause, traditional activation functions such as the hyperbolic tangent function have gradients in the range [-1,1], and backpropagation computes gradients by the chain rule. This has the effect of multiplying n of these small numbers to compute gradients of the early layers in an n-layer network, meaning that the gradient decreases exponentially with n while the early layers train very slowly.

A generative adversarial network (GAN) is a class of machine learning frameworks and a prominent framework for approaching generative AI. The concept was initially developed by Ian Goodfellow and his colleagues in June 2014. In a GAN, two neural networks contest with each other in the form of a zero-sum game, where one agent's gain is another agent's loss.

A transformer is a deep learning architecture developed by Google and based on the multi-head attention mechanism, proposed in a 2017 paper "Attention Is All You Need". It has no recurrent units, and thus requires less training time than previous recurrent neural architectures, such as long short-term memory (LSTM), and its later variation has been prevalently adopted for training large language models (LLM) on large (language) datasets, such as the Wikipedia corpus and Common Crawl. Text is converted to numerical representations called tokens, and each token is converted into a vector via looking up from a word embedding table. At each layer, each token is then contextualized within the scope of the context window with other (unmasked) tokens via a parallel multi-head attention mechanism allowing the signal for key tokens to be amplified and less important tokens to be diminished. The transformer paper, published in 2017, is based on the softmax-based attention mechanism proposed by Bahdanau et. al. in 2014 for machine translation, and the Fast Weight Controller, similar to a transformer, proposed in 1992.

In machine learning, a variational autoencoder (VAE) is an artificial neural network architecture introduced by Diederik P. Kingma and Max Welling. It is part of the families of probabilistic graphical models and variational Bayesian methods.
An energy-based model (EBM) (also called a Canonical Ensemble Learning(CEL) or Learning via Canonical Ensemble (LCE)) is an application of canonical ensemble formulation of statistical physics for learning from data problems. The approach prominently appears in generative models (GMs).
In machine learning, diffusion models, also known as diffusion probabilistic models or score-based generative models, are a class of latent variable generative models. A diffusion model consists of three major components: the forward process, the reverse process, and the sampling procedure. The goal of diffusion models is to learn a diffusion process that generates a probability distribution for a given dataset from which we can then sample new images. They learn the latent structure of a dataset by modeling the way in which data points diffuse through their latent space.
























































































