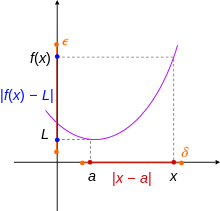
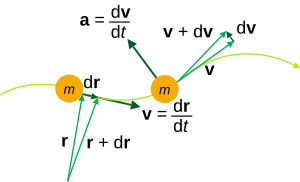
The derivative is a fundamental tool of calculus that quantifies the sensitivity of change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation.

In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field whose value at a point gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of . If the gradient of a function is non-zero at a point , the direction of the gradient is the direction in which the function increases most quickly from , and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function may be defined by:
In mathematics, and more specifically in linear algebra, a linear map is a mapping between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism.

In mathematics, the mean value theorem states, roughly, that for a given planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints. It is one of the most important results in real analysis. This theorem is used to prove statements about a function on an interval starting from local hypotheses about derivatives at points of the interval.
In mathematics, an operator is generally a mapping or function that acts on elements of a space to produce elements of another space. There is no general definition of an operator, but the term is often used in place of function when the domain is a set of functions or other structured objects. Also, the domain of an operator is often difficult to characterize explicitly, and may be extended so as to act on related objects. See Operator (physics) for other examples.

In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample.

A Fourier series is an expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series, but not all trigonometric series are Fourier series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always converge. Well-behaved functions, for example smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric functions, described in Common forms of the Fourier series below.

In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space . A vector field on a plane can be visualized as a collection of arrows with given magnitudes and directions, each attached to a point on the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout three dimensional space, such as the wind, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point.
A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula. As formulas are entirely constituted with symbols of various types, many symbols are needed for expressing all mathematics.

In geometry, a normal is an object that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the line perpendicular to the tangent line to the curve at the point.
In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.

In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A differentiable function is smooth and does not contain any break, angle, or cusp.

In mathematics, the Legendre transformation, first introduced by Adrien-Marie Legendre in 1787 when studying the minimal surface problem, is an involutive transformation on real-valued functions that are convex on a real variable. Specifically, if a real-valued multivariable function is convex on one of its independent real variables, then the Legendre transform with respect to this variable is applicable to the function.
Multivariable calculus is the extension of calculus in one variable to calculus with functions of several variables: the differentiation and integration of functions involving multiple variables (multivariate), rather than just one.
In mathematics, a homogeneous function is a function of several variables such that the following holds: If each of the function's arguments is multiplied by the same scalar, then the function's value is multiplied by some power of this scalar; the power is called the degree of homogeneity, or simply the degree. That is, if k is an integer, a function f of n variables is homogeneous of degree k if

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.

In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function. Thus it provides an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There are particularly simple results for the characteristic functions of distributions defined by the weighted sums of random variables.
A vector-valued function, also referred to as a vector function, is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector ; the dimension of the function's domain has no relation to the dimension of its range.
In mathematics, the Malliavin derivative is a notion of derivative in the Malliavin calculus. Intuitively, it is the notion of derivative appropriate to paths in classical Wiener space, which are "usually" not differentiable in the usual sense.
In mathematical analysis and its applications, a function of several real variables or real multivariate function is a function with more than one argument, with all arguments being real variables. This concept extends the idea of a function of a real variable to several variables. The "input" variables take real values, while the "output", also called the "value of the function", may be real or complex. However, the study of the complex-valued functions may be easily reduced to the study of the real-valued functions, by considering the real and imaginary parts of the complex function; therefore, unless explicitly specified, only real-valued functions will be considered in this article.