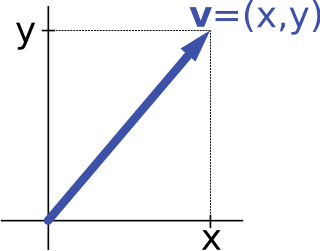In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square.

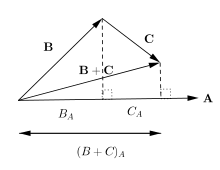
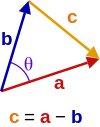
In mathematics, physics, and engineering, a Euclidean vector or simply a vector is a geometric object that has magnitude and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a directed line segment, or graphically as an arrow connecting an initial pointA with a terminal pointB, and denoted by

In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices A and B is denoted as AB.

In mathematics, the cross product or vector product is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space, and is denoted by the symbol . Given two linearly independent vectors a and b, the cross product, a × b, is a vector that is perpendicular to both a and b, and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product.
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).
Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space. Specifically, they encode information about an axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and crystallographic texture analysis.
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal unit vectors. A unit vector means that the vector has a length of 1, which is also known as normalized. Orthogonal means that the vectors are all perpendicular to each other. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length. An orthonormal set which forms a basis is called an orthonormal basis.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric tensor on M consists of a metric tensor at each point p of M that varies smoothly with p.
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix
Screw theory is the algebraic calculation of pairs of vectors, such as angular and linear velocity, or forces and moments, that arise in the kinematics and dynamics of rigid bodies.

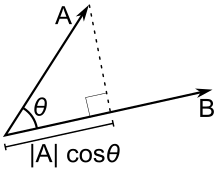
The vector projection of a vector a on a nonzero vector b is the orthogonal projection of a onto a straight line parallel to b. The projection of a onto b is often written as or a∥b.

In geometry and linear algebra, a Cartesian tensor uses an orthonormal basis to represent a tensor in a Euclidean space in the form of components. Converting a tensor's components from one such basis to another is done through an orthogonal transformation.
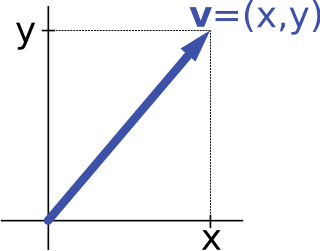
In mathematics and physics, vector notation is a commonly used notation for representing vectors, which may be Euclidean vectors, or more generally, members of a vector space.
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.
In data analysis, cosine similarity is a measure of similarity between two non-zero vectors defined in an inner product space. Cosine similarity is the cosine of the angle between the vectors; that is, it is the dot product of the vectors divided by the product of their lengths. It follows that the cosine similarity does not depend on the magnitudes of the vectors, but only on their angle. The cosine similarity always belongs to the interval For example, two proportional vectors have a cosine similarity of 1, two orthogonal vectors have a similarity of 0, and two opposite vectors have a similarity of -1. In some contexts, the component values of the vectors cannot be negative, in which case the cosine similarity is bounded in .

In mathematics, the axis–angle representation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector e indicating the direction (geometry) of an axis of rotation, and an angle of rotation θ describing the magnitude and sense of the rotation about the axis. Only two numbers, not three, are needed to define the direction of a unit vector e rooted at the origin because the magnitude of e is constrained. For example, the elevation and azimuth angles of e suffice to locate it in any particular Cartesian coordinate frame.
In mathematics, specifically multilinear algebra, a dyadic or dyadic tensor is a second order tensor, written in a notation that fits in with vector algebra.

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
The following are important identities in vector algebra. Identities that involve the magnitude of a vector , or the dot product of two vectors A·B, apply to vectors in any dimension. Identities that use the cross product A×B are defined only in three dimensions. Most of these relations can be dated to Josiah Willard Gibbs, founder of vector calculus, if not earlier.
The concept of angles between lines, between two planes or between a line and a plane can be generalized to arbitrary dimensions. This generalization was first discussed by Camille Jordan. For any pair of flats in a Euclidean space of arbitrary dimension one can define a set of mutual angles which are invariant under isometric transformation of the Euclidean space. If the flats do not intersect, their shortest distance is one more invariant. These angles are called canonical or principal. The concept of angles can be generalized to pairs of flats in a finite-dimensional inner product space over the complex numbers.