
The travelling salesman problem (TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.

Bucket sort, or bin sort, is a sorting algorithm that works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a distribution sort, a generalization of pigeonhole sort that allows multiple keys per bucket, and is a cousin of radix sort in the most-to-least significant digit flavor. Bucket sort can be implemented with comparisons and therefore can also be considered a comparison sort algorithm. The computational complexity depends on the algorithm used to sort each bucket, the number of buckets to use, and whether the input is uniformly distributed.
Golomb coding is a lossless data compression method using a family of data compression codes invented by Solomon W. Golomb in the 1960s. Alphabets following a geometric distribution will have a Golomb code as an optimal prefix code, making Golomb coding highly suitable for situations in which the occurrence of small values in the input stream is significantly more likely than large values.
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equation constraints. It is named after the mathematician Joseph-Louis Lagrange. The basic idea is to convert a constrained problem into a form such that the derivative test of an unconstrained problem can still be applied. The relationship between the gradient of the function and gradients of the constraints rather naturally leads to a reformulation of the original problem, known as the Lagrangian function.

Distributed.net is a volunteer computing effort that is attempting to solve large scale problems using otherwise idle CPU or GPU time. It is governed by Distributed Computing Technologies, Incorporated (DCTI), a non-profit organization under U.S. tax code 501(c)(3).
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications especially in ranking problems such as feedback arc set. Topological sorting is possible even when the DAG has disconnected components.
In computer science, a suffix array is a sorted array of all suffixes of a string. It is a data structure used in, among others, full-text indices, data-compression algorithms, and the field of bibliometrics.
A perfect ruler of length is a ruler with integer markings , for which there exists an integer such that any positive integer is uniquely expressed as the difference for some . This is referred to as an -perfect ruler.

In data compression, a universal code for integers is a prefix code that maps the positive integers onto binary codewords, with the additional property that whatever the true probability distribution on integers, as long as the distribution is monotonic (i.e., p(i) ≥ p(i + 1) for all positive i), the expected lengths of the codewords are within a constant factor of the expected lengths that the optimal code for that probability distribution would have assigned. A universal code is asymptotically optimal if the ratio between actual and optimal expected lengths is bounded by a function of the information entropy of the code that, in addition to being bounded, approaches 1 as entropy approaches infinity.
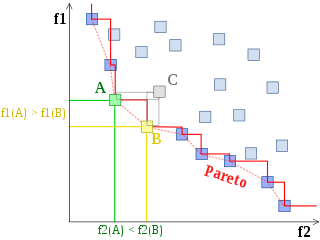
In multi-objective optimization, the Pareto front is the set of all Pareto efficient solutions. The concept is widely used in engineering. It allows the designer to restrict attention to the set of efficient choices, and to make tradeoffs within this set, rather than considering the full range of every parameter.
In information theory and computer science, the Damerau–Levenshtein distance is a string metric for measuring the edit distance between two sequences. Informally, the Damerau–Levenshtein distance between two words is the minimum number of operations required to change one word into the other.
In computer science, the longest increasing subsequence problem aims to find a subsequence of a given sequence in which the subsequence's elements are sorted in an ascending order and in which the subsequence is as long as possible. This subsequence is not necessarily contiguous or unique. The longest increasing subsequences are studied in the context of various disciplines related to mathematics, including algorithmics, random matrix theory, representation theory, and physics. The longest increasing subsequence problem is solvable in time where denotes the length of the input sequence.
Optimal job scheduling is a class of optimization problems related to scheduling. The inputs to such problems are a list of jobs and a list of machines. The required output is a schedule – an assignment of jobs to machines. The schedule should optimize a certain objective function. In the literature, problems of optimal job scheduling are often called machine scheduling, processor scheduling, multiprocessor scheduling, or just scheduling.
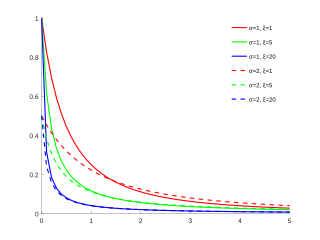
In statistics, the generalized Pareto distribution (GPD) is a family of continuous probability distributions. It is often used to model the tails of another distribution. It is specified by three parameters: location , scale , and shape . Sometimes it is specified by only scale and shape and sometimes only by its shape parameter. Some references give the shape parameter as .
In mathematics, the Golomb–Dickman constant arises in the theory of random permutations and in number theory. Its value is
In number theory, a Sidon sequence is a sequence of natural numbers in which all pairwise sums are different. Sidon sequences are also called Sidon sets; they are named after the Hungarian mathematician Simon Sidon, who introduced the concept in his investigations of Fourier series.
A sparse ruler is a ruler in which some of the distance marks may be missing. More abstractly, a sparse ruler of length with marks is a sequence of integers where . The marks and correspond to the ends of the ruler. In order to measure the distance , with there must be marks and such that .
In computer science, the reduction operator is a type of operator that is commonly used in parallel programming to reduce the elements of an array into a single result. Reduction operators are associative and often commutative. The reduction of sets of elements is an integral part of programming models such as Map Reduce, where a reduction operator is applied (mapped) to all elements before they are reduced. Other parallel algorithms use reduction operators as primary operations to solve more complex problems. Many reduction operators can be used for broadcasting to distribute data to all processors.
The quadratic knapsack problem (QKP), first introduced in 19th century, is an extension of knapsack problem that allows for quadratic terms in the objective function: Given a set of items, each with a weight, a value, and an extra profit that can be earned if two items are selected, determine the number of items to include in a collection without exceeding capacity of the knapsack, so as to maximize the overall profit. Usually, quadratic knapsack problems come with a restriction on the number of copies of each kind of item: either 0, or 1. This special type of QKP forms the 0-1 quadratic knapsack problem, which was first discussed by Gallo et al. The 0-1 quadratic knapsack problem is a variation of knapsack problems, combining the features of unbounded knapsack problem, 0-1 knapsack problem and quadratic knapsack problem.
In functional analysis and related areas of mathematics, a complete topological vector space is a topological vector space (TVS) with the property that whenever points get progressively closer to each other, then there exists some point towards which they all get closer. The notion of "points that get progressively closer" is made rigorous by Cauchy nets or Cauchy filters, which are generalizations of Cauchy sequences, while "point towards which they all get closer" means that this Cauchy net or filter converges to The notion of completeness for TVSs uses the theory of uniform spaces as a framework to generalize the notion of completeness for metric spaces. But unlike metric-completeness, TVS-completeness does not depend on any metric and is defined for all TVSs, including those that are not metrizable or Hausdorff.
















![Example of a conference room with proportions of a [0, 2, 7, 8, 11] Golomb ruler, making it configurable to 10 different sizes. Golomb ruler conference room.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/5/52/Golomb_ruler_conference_room.svg/300px-Golomb_ruler_conference_room.svg.png)






