
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

In geometry and group theory, a lattice in the real coordinate space is an infinite set of points in this space with the properties that coordinatewise addition or subtraction of two points in the lattice produces another lattice point, that the lattice points are all separated by some minimum distance, and that every point in the space is within some maximum distance of a lattice point. Closure under addition and subtraction means that a lattice must be a subgroup of the additive group of the points in the space, and the requirements of minimum and maximum distance can be summarized by saying that a lattice is a Delone set. More abstractly, a lattice can be described as a free abelian group of dimension which spans the vector space . For any basis of , the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice, and every lattice can be formed from a basis in this way. A lattice may be viewed as a regular tiling of a space by a primitive cell.

The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.

In mathematics, the "happy ending problem" is the following statement:
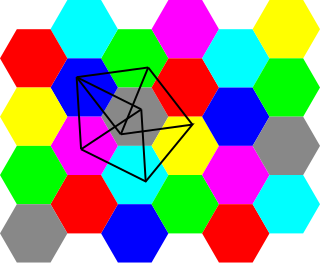
In geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance 1 from each other have the same color. The answer is unknown, but has been narrowed down to one of the numbers 5, 6 or 7. The correct value may depend on the choice of axioms for set theory.
In arithmetic geometry, the Bombieri–Lang conjecture is an unsolved problem conjectured by Enrico Bombieri and Serge Lang about the Zariski density of the set of rational points of an algebraic variety of general type.

In mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one. To distinguish these graphs from the larger family of their subgraphs, they may be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are subgraphs of unit distance graphs.
In additive number theory, Kemnitz's conjecture states that every set of lattice points in the plane has a large subset whose centroid is also a lattice point. It was proved independently in the autumn of 2003 by Christian Reiher, then an undergraduate student, and Carlos di Fiore, then a high school student.

In mathematics, the equilateral dimension of a metric space is the maximum size of any subset of the space whose points are all at equal distances to each other. Equilateral dimension has also been called "metric dimension", but the term "metric dimension" also has many other inequivalent usages. The equilateral dimension of a -dimensional Euclidean space is , achieved by a regular simplex, and the equilateral dimension of a -dimensional vector space with the Chebyshev distance is , achieved by a hypercube. However, the equilateral dimension of a space with the Manhattan distance is not known; Kusner's conjecture, named after Robert B. Kusner, states that it is exactly , achieved by a cross polytope.
In geometry, the moment curve is an algebraic curve in d-dimensional Euclidean space given by the set of points with Cartesian coordinates of the form
In discrete geometry, the Erdős distinct distances problem states that every set of points in the plane has a nearly-linear number of distinct distances. It was posed by Paul Erdős in 1946 and almost proven by Larry Guth and Nets Katz in 2015.
In geometric measure theory, Falconer's conjecture, named after Kenneth Falconer, is an unsolved problem concerning the sets of Euclidean distances between points in compact -dimensional spaces. Intuitively, it states that a set of points that is large in its Hausdorff dimension must determine a set of distances that is large in measure. More precisely, if is a compact set of points in -dimensional Euclidean space whose Hausdorff dimension is strictly greater than , then the conjecture states that the set of distances between pairs of points in must have nonzero Lebesgue measure.
In discrete and computational geometry, a set of points in the Euclidean plane or a higher-dimensional Euclidean space is said to be in convex position or convex independent if none of the points can be represented as a convex combination of the others. A finite set of points is in convex position if all of the points are vertices of their convex hull. More generally, a family of convex sets is said to be in convex position if they are pairwise disjoint and none of them is contained in the convex hull of the others.
In mathematics, the Erdős–Ulam problem asks whether the plane contains a dense set of points whose Euclidean distances are all rational numbers. It is named after Paul Erdős and Stanislaw Ulam.

In discrete geometry, an isosceles set is a set of points with the property that every three of them form an isosceles triangle. More precisely, each three points should determine at most two distances; this also allows degenerate isosceles triangles formed by three equally-spaced points on a line.

József Solymosi is a Hungarian-Canadian mathematician and a professor of mathematics at the University of British Columbia. His main research interests are arithmetic combinatorics, discrete geometry, graph theory, and combinatorial number theory.
Ilona Palásti (1924–1991) was a Hungarian mathematician who worked at the Alfréd Rényi Institute of Mathematics. She is known for her research in discrete geometry, geometric probability, and the theory of random graphs. With Alfréd Rényi and others, she was considered to be one of the members of the Hungarian School of Probability.

Blichfeldt's theorem is a mathematical theorem in the geometry of numbers, stating that whenever a bounded set in the Euclidean plane has area , it can be translated so that it includes at least points of the integer lattice. Equivalently, every bounded set of area contains a set of points whose coordinates all differ by integers.












