In fractal geometry, the H tree is a fractal tree structure constructed from perpendicular line segments, each smaller by a factor of the square root of 2 from the next larger adjacent segment. It is so called because its repeating pattern resembles the letter "H". It has Hausdorff dimension 2, and comes arbitrarily close to every point in a rectangle. Its applications include VLSI design and microwave engineering.
An H tree can be constructed by starting with a line segment of arbitrary length, drawing two shorter segments at right angles to the first through its endpoints, and continuing in the same vein, reducing (dividing) the length of the line segments drawn at each stage by . [1] A variant of this construction could also be defined in which the length at each iteration is multiplied by a ratio less than , but for this variant the resulting shape covers only part of its bounding rectangle, with a fractal boundary. [2]
An alternative process that generates the same fractal set is to begin with a rectangle with sides in the ratio , and repeatedly bisect it into two smaller silver rectangles, at each stage connecting the two centroids of the two smaller rectangles by a line segment. A similar process can be performed with rectangles of any other shape, but the rectangle leads to the line segment size decreasing uniformly by a factor at each step while for other rectangles the length will decrease by different factors at odd and even levels of the recursive construction.
The H tree is a self-similar fractal; its Hausdorff dimension is equal to 2. [2]
The points of the H tree come arbitrarily close to every point in a rectangle (the same as the starting rectangle in the constructing by centroids of subdivided rectangles). However, it does not include all points of the rectangle; for instance, the points on the perpendicular bisector of the initial line segment (other than the midpoint of this segment) are not included.
In VLSI design, the H tree may be used as the layout for a complete binary tree using a total area that is proportional to the number of nodes of the tree. [3] Additionally, the H tree forms a space efficient layout for trees in graph drawing, [4] and as part of a construction of a point set for which the sum of squared edge lengths of the traveling salesman tour is large. [5] It is commonly used as a clock distribution network for routing timing signals to all parts of a chip with equal propagation delays to each part, [6] and has also been used as an interconnection network for VLSI multiprocessors. [7]
The planar H tree can be generalized to the three-dimensional structure via adding line segments on the direction perpendicular to the H tree plane. [8] The resultant three-dimensional H tree has Hausdorff dimension equal to 3. The planar H tree and its three-dimensional version have been found to constitute artificial electromagnetic atoms in photonic crystals and metamaterials and might have potential applications in microwave engineering. [8]
The H tree is an example of a fractal canopy, in which the angle between neighboring line segments is always 180 degrees. In its property of coming arbitrarily close to every point of its bounding rectangle, it also resembles a space-filling curve, although it is not itself a curve.
Topologically, an H tree has properties similar to those of a dendroid. However, they are not dendroids: dendroids must be closed sets, and H trees are not closed (their closure is the whole rectangle).
Variations of the same tree structure with thickened polygonal branches in place of the line segments of the H tree have been defined by Benoit Mandelbrot, and are sometimes called the Mandelbrot tree. In these variations, to avoid overlaps between the leaves of the tree and their thickened branches, the scale factor by which the size is reduced at each level must be slightly greater than . [9]
In mathematics, Hausdorff dimension is a measure of roughness, or more specifically, fractal dimension, that was introduced in 1918 by mathematician Felix Hausdorff. For instance, the Hausdorff dimension of a single point is zero, of a line segment is 1, of a square is 2, and of a cube is 3. That is, for sets of points that define a smooth shape or a shape that has a small number of corners—the shapes of traditional geometry and science—the Hausdorff dimension is an integer agreeing with the usual sense of dimension, also known as the topological dimension. However, formulas have also been developed that allow calculation of the dimension of other less simple objects, where, solely on the basis of their properties of scaling and self-similarity, one is led to the conclusion that particular objects—including fractals—have non-integer Hausdorff dimensions. Because of the significant technical advances made by Abram Samoilovitch Besicovitch allowing computation of dimensions for highly irregular or "rough" sets, this dimension is also commonly referred to as the Hausdorff–Besicovitch dimension.
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices , , and is sometimes denoted as .
The Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal attractive fixed set with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.
The Koch snowflake is a fractal curve and one of the earliest fractals to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled "On a Continuous Curve Without Tangents, Constructible from Elementary Geometry" by the Swedish mathematician Helge von Koch.
In mathematics, the Menger sponge is a fractal curve. It is a three-dimensional generalization of the one-dimensional Cantor set and two-dimensional Sierpinski carpet. It was first described by Karl Menger in 1926, in his studies of the concept of topological dimension.
In mathematical analysis, a space-filling curve is a curve whose range reaches every point in a higher dimensional region, typically the unit square. Because Giuseppe Peano (1858–1932) was the first to discover one, space-filling curves in the 2-dimensional plane are sometimes called Peano curves, but that phrase also refers to the Peano curve, the specific example of a space-filling curve found by Peano.
A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems. The dragon curve is probably most commonly thought of as the shape that is generated from repeatedly folding a strip of paper in half, although there are other curves that are called dragon curves that are generated differently.
In mathematics, Hausdorff measure is a generalization of the traditional notions of area and volume to non-integer dimensions, specifically fractals and their Hausdorff dimensions. It is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in or, more generally, in any metric space.
In mathematics, a Kakeya set, or Besicovitch set, is a set of points in Euclidean space which contains a unit line segment in every direction. For instance, a disk of radius 1/2 in the Euclidean plane, or a ball of radius 1/2 in three-dimensional space, forms a Kakeya set. Much of the research in this area has studied the problem of how small such sets can be. Besicovitch showed that there are Besicovitch sets of measure zero.
In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. It is a circular arc that measures 180°. It has only one line of symmetry.
In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Problems of counting the features of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.
In probability theory, the Schramm–Loewner evolution with parameter κ, also known as stochastic Loewner evolution (SLEκ), is a family of random planar curves that have been proven to be the scaling limit of a variety of two-dimensional lattice models in statistical mechanics. Given a parameter κ and a domain in the complex plane U, it gives a family of random curves in U, with κ controlling how much the curve turns. There are two main variants of SLE, chordal SLE which gives a family of random curves from two fixed boundary points, and radial SLE, which gives a family of random curves from a fixed boundary point to a fixed interior point. These curves are defined to satisfy conformal invariance and a domain Markov property.
In graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.
In Euclidean geometry, Varignon's theorem holds that the midpoints of the sides of an arbitrary quadrilateral form a parallelogram, called the Varignon parallelogram. It is named after Pierre Varignon, whose proof was published posthumously in 1731.
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of vertices from an n-vertex graph can partition the graph into disjoint subgraphs each of which has at most vertices.
In computational geometry, the largest empty rectangle problem,maximal empty rectangle problem or maximum empty rectangle problem, is the problem of finding a rectangle of maximal size to be placed among obstacles in the plane. There are a number of variants of the problem, depending on the particularities of this generic formulation, in particular, depending on the measure of the "size", domain, and the orientation of the rectangle.
In discrete geometry, an opaque set is a system of curves or other set in the plane that blocks all lines of sight across a polygon, circle, or other shape. Opaque sets have also been called barriers, beam detectors, opaque covers, or opaque forests. Opaque sets were introduced by Stefan Mazurkiewicz in 1916, and the problem of minimizing their total length was posed by Frederick Bagemihl in 1959.
A geometric separator is a line that partitions a collection of geometric shapes into two subsets, such that proportion of shapes in each subset is bounded, and the number of shapes that do not belong to any subset is small.
The Fibonacci word fractal is a fractal curve defined on the plane from the Fibonacci word.
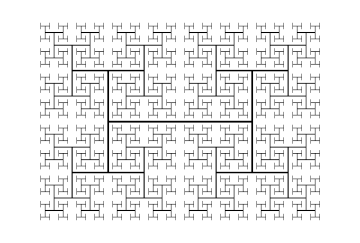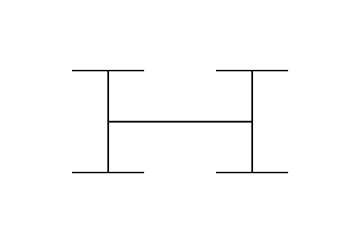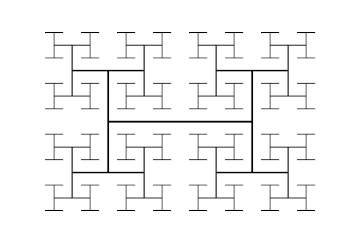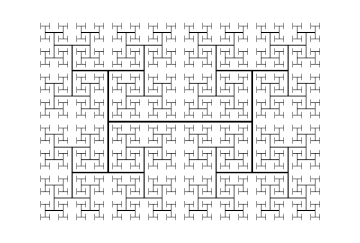
The Minkowski sausage or Minkowski curve is a fractal first proposed by and named for Hermann Minkowski as well as its casual resemblance to a sausage or sausage links. The initiator is a line segment and the generator is a broken line of eight parts one fourth the length.
