In mathematics, fractal is a term used to describe geometric shapes containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory.

In mathematics, Hausdorff dimension is a measure of roughness, or more specifically, fractal dimension, that was first introduced in 1918 by mathematician Felix Hausdorff. For instance, the Hausdorff dimension of a single point is zero, of a line segment is 1, of a square is 2, and of a cube is 3. That is, for sets of points that define a smooth shape or a shape that has a small number of corners—the shapes of traditional geometry and science—the Hausdorff dimension is an integer agreeing with the usual sense of dimension, also known as the topological dimension. However, formulas have also been developed that allow calculation of the dimension of other less simple objects, where, solely on the basis of their properties of scaling and self-similarity, one is led to the conclusion that particular objects—including fractals—have non-integer Hausdorff dimensions. Because of the significant technical advances made by Abram Samoilovitch Besicovitch allowing computation of dimensions for highly irregular or "rough" sets, this dimension is also commonly referred to as the Hausdorff–Besicovitch dimension.

The Mandelbrot set is the set of complex numbers for which the function does not diverge to infinity when iterated from , i.e., for which the sequence , , etc., remains bounded in absolute value.

The Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal attractive fixed set with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.

The Koch snowflake is a fractal curve and one of the earliest fractals to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled "On a Continuous Curve Without Tangents, Constructible from Elementary Geometry" by the Swedish mathematician Helge von Koch.

In mathematics, the Menger sponge is a fractal curve. It is a three-dimensional generalization of the one-dimensional Cantor set and two-dimensional Sierpinski carpet. It was first described by Karl Menger in 1926, in his studies of the concept of topological dimension.
In mathematics, more specifically in fractal geometry, a fractal dimension is a ratio providing a statistical index of complexity comparing how detail in a pattern changes with the scale at which it is measured. It has also been characterized as a measure of the space-filling capacity of a pattern that tells how a fractal scales differently from the space it is embedded in; a fractal dimension does not have to be an integer.

In mathematics, the Weierstrass function is an example of a real-valued function that is continuous everywhere but differentiable nowhere. It is an example of a fractal curve. It is named after its discoverer Karl Weierstrass.
This is a list of fractal topics, by Wikipedia page, See also list of dynamical systems and differential equations topics.
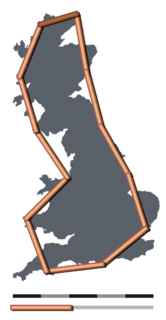
"How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension" is a paper by mathematician Benoît Mandelbrot, first published in Science on 5 May 1967. In this paper, Mandelbrot discusses self-similar curves that have Hausdorff dimension between 1 and 2. These curves are examples of fractals, although Mandelbrot does not use this term in the paper, as he did not coin it until 1975. The paper is one of Mandelbrot's first publications on the topic of fractals.

The Gosper curve, also known as Peano-Gosper Curve, named after Bill Gosper, also known as the flowsnake, is a space-filling curve whose limit set is rep-7. It is a fractal curve similar in its construction to the dragon curve and the Hilbert curve.

Mitsuhiro Shishikura is a Japanese mathematician working in the field of complex dynamics. He is professor at Kyoto University in Japan.

A fractal curve is, loosely, a mathematical curve whose shape retains the same general pattern of irregularity, regardless of how high it is magnified, that is, its graph takes the form of a fractal. In general, fractal curves are nowhere rectifiable curves — that is, they do not have finite length — and every subarc longer than a single point has infinite length.

The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal curve-like properties of coastlines, i.e., the fact that a coastline typically has a fractal dimension. The first recorded observation of this phenomenon was by Lewis Fry Richardson and it was expanded upon by Benoit Mandelbrot.

A teragon is a polygon with an infinite number of sides, the most famous example being the Koch snowflake. The term was coined by Benoît Mandelbrot from the words Classical Greek τέρας + γωνία. Typically, a teragon will be bounded by one or more self-similar fractal curves, which are created by replacing each line segment in an initial figure with multiple connected segments, then replacing each of those segments with the same pattern of segments, then repeating the process an infinite number of times for every line segment in the figure.

Fractal-generating software is any type of graphics software that generates images of fractals. There are many fractal generating programs available, both free and commercial. Mobile apps are available to play or tinker with fractals. Some programmers create fractal software for themselves because of the novelty and because of the challenge in understanding the related mathematics. The generation of fractals has led to some very large problems for pure mathematics.

In mathematics the Vicsek fractal, also known as Vicsek snowflake or box fractal, is a fractal arising from a construction similar to that of the Sierpinski carpet, proposed by Tamás Vicsek. It has applications including as compact antennas, particularly in cellular phones.
An n-flake, polyflake, or Sierpinski n-gon, is a fractal constructed starting from an n-gon. This n-gon is replaced by a flake of smaller n-gons, such that the scaled polygons are placed at the vertices, and sometimes in the center. This process is repeated recursively to result in the fractal. Typically, there is also the restriction that the n-gons must touch yet not overlap.

In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of Scientific American. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in Mathematics Magazine.