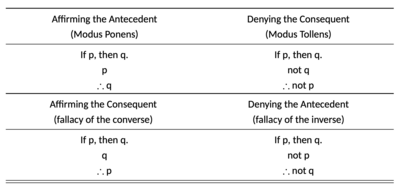
In propositional logic, affirming the consequent, sometimes called converse error, fallacy of the converse, or confusion of necessity and sufficiency, is a formal fallacy of taking a true conditional statement under certain assumptions, and invalidly inferring its converse, even though that statement may not be true under the same assumptions. This arises when the consequent has other possible antecedents.
In classical logic, disjunctive syllogism is a valid argument form which is a syllogism having a disjunctive statement for one of its premises.
The propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. It deals with propositions and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives representing the truth functions of conjunction, disjunction, implication, equivalence, and negation. Some sources include other connectives, as in the table below.
In propositional logic, modus ponens, also known as modus ponendo ponens, implication elimination, or affirming the antecedent, is a deductive argument form and rule of inference. It can be summarized as "P implies Q.P is true. Therefore, Q must also be true."
In propositional logic, modus tollens (MT), also known as modus tollendo tollens and denying the consequent, is a deductive argument form and a rule of inference. Modus tollens is a mixed hypothetical syllogism that takes the form of "If P, then Q. Not Q. Therefore, not P." It is an application of the general truth that if a statement is true, then so is its contrapositive. The form shows that inference from P implies Q to the negation of Q implies the negation of P is a valid argument.
Deductive reasoning is the mental process of drawing deductive inferences. An inference is deductively valid if its conclusion follows logically from its premises, i.e. it is impossible for the premises to be true and the conclusion to be false.
Denying the antecedent, sometimes also called inverse error or fallacy of the inverse, is a formal fallacy of inferring the inverse from an original statement. It is a type of mixed hypothetical syllogism in the form:
Intuitionistic logic, sometimes more generally called constructive logic, refers to systems of symbolic logic that differ from the systems used for classical logic by more closely mirroring the notion of constructive proof. In particular, systems of intuitionistic logic do not assume the law of the excluded middle and double negation elimination, which are fundamental inference rules in classical logic.
In propositional logic, double negation is the theorem that states that "If a statement is true, then it is not the case that the statement is not true." This is expressed by saying that a proposition A is logically equivalent to not (not-A), or by the formula A ≡ ~(~A) where the sign ≡ expresses logical equivalence and the sign ~ expresses negation.
In mathematical logic, a deduction theorem is a metatheorem that justifies doing conditional proofs from a hypothesis in systems that do not explicitly axiomatize that hypothesis, i.e. to prove an implication A → B, it is sufficient to assume A as a hypothesis and then proceed to derive B. Deduction theorems exist for both propositional logic and first-order logic. The deduction theorem is an important tool in Hilbert-style deduction systems because it permits one to write more comprehensible and usually much shorter proofs than would be possible without it. In certain other formal proof systems the same conveniency is provided by an explicit inference rule; for example natural deduction calls it implication introduction.

The material conditional is an operation commonly used in logic. When the conditional symbol is interpreted as material implication, a formula is true unless is true and is false. Material implication can also be characterized inferentially by modus ponens, modus tollens, conditional proof, and classical reductio ad absurdum.
An antecedent is the first half of a hypothetical proposition, whenever the if-clause precedes the then-clause. In some contexts the antecedent is called the protasis.
Constructive dilemma is a valid rule of inference of propositional logic. It is the inference that, if P implies Q and R implies S and either P or R is true, then either Q or S has to be true. In sum, if two conditionals are true and at least one of their antecedents is, then at least one of their consequents must be too. Constructive dilemma is the disjunctive version of modus ponens, whereas, destructive dilemma is the disjunctive version of modus tollens. The constructive dilemma rule can be stated:
Destructive dilemma is the name of a valid rule of inference of propositional logic. It is the inference that, if P implies Q and R implies S and either Q is false or S is false, then either P or R must be false. In sum, if two conditionals are true, but one of their consequents is false, then one of their antecedents has to be false. Destructive dilemma is the disjunctive version of modus tollens. The disjunctive version of modus ponens is the constructive dilemma. The destructive dilemma rule can be stated:
In propositional logic, transposition is a valid rule of replacement that permits one to switch the antecedent with the consequent of a conditional statement in a logical proof if they are also both negated. It is the inference from the truth of "A implies B" to the truth of "Not-B implies not-A", and conversely. It is very closely related to the rule of inference modus tollens. It is the rule that
In mathematical logic, the implicational propositional calculus is a version of classical propositional calculus that uses only one connective, called implication or conditional. In formulas, this binary operation is indicated by "implies", "if ..., then ...", "→", "", etc..
In logic, especially mathematical logic, a Hilbert system, sometimes called Hilbert calculus, Hilbert-style deductive system or Hilbert–Ackermann system, is a type of system of formal deduction attributed to Gottlob Frege and David Hilbert. These deductive systems are most often studied for first-order logic, but are of interest for other logics as well.
In logic and mathematics, contraposition refers to the inference of going from a conditional statement into its logically equivalent contrapositive, and an associated proof method known as proof by contraposition. The contrapositive of a statement has its antecedent and consequent inverted and flipped.
Exportation is a valid rule of replacement in propositional logic. The rule allows conditional statements having conjunctive antecedents to be replaced by statements having conditional consequents and vice versa in logical proofs. It is the rule that: