Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.
Maurits Cornelis Escher was a Dutch graphic artist who made woodcuts, lithographs, and mezzotints, many of which were inspired by mathematics. Despite wide popular interest, for most of his life Escher was neglected in the art world, even in his native Netherlands. He was 70 before a retrospective exhibition was held. In the late twentieth century, he became more widely appreciated, and in the twenty-first century he has been celebrated in exhibitions around the world.
In visual perception, an optical illusion is an illusion caused by the visual system and characterized by a visual percept that arguably appears to differ from reality. Illusions come in a wide variety; their categorization is difficult because the underlying cause is often not clear but a classification proposed by Richard Gregory is useful as an orientation. According to that, there are three main classes: physical, physiological, and cognitive illusions, and in each class there are four kinds: Ambiguities, distortions, paradoxes, and fictions. A classical example for a physical distortion would be the apparent bending of a stick half immerged in water; an example for a physiological paradox is the motion aftereffect. An example for a physiological fiction is an afterimage. Three typical cognitive distortions are the Ponzo, Poggendorff, and Müller-Lyer illusion. Physical illusions are caused by the physical environment, e.g. by the optical properties of water. Physiological illusions arise in the eye or the visual pathway, e.g. from the effects of excessive stimulation of a specific receptor type. Cognitive visual illusions are the result of unconscious inferences and are perhaps those most widely known.
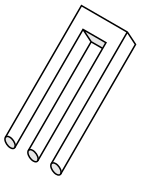
The Penrose triangle, also known as the Penrose tribar, the impossible tribar, or the impossible triangle, is a triangular impossible object, an optical illusion consisting of an object which can be depicted in a perspective drawing, but cannot exist as a solid object. It was first created by the Swedish artist Oscar Reutersvärd in 1934. Independently from Reutersvärd, the triangle was devised and popularized in the 1950s by psychiatrist Lionel Penrose and his son, prominent Nobel Prize-winning mathematician Sir Roger Penrose, who described it as "impossibility in its purest form". It is featured prominently in the works of artist M. C. Escher, whose earlier depictions of impossible objects partly inspired it.
The Necker cube is an optical illusion that was first published as a rhomboid in 1832 by Swiss crystallographer Louis Albert Necker. It is a simple wire-frame, two dimensional drawing of a cube with no visual cues as to its orientation, so it can be interpreted to have either the lower-left or the upper-right square as its front side.
The impossible cube or irrational cube is an impossible object invented by M.C. Escher for his print Belvedere. It is a two-dimensional figure that superficially resembles a perspective drawing of a three-dimensional cube, with its features drawn inconsistently from the way they would appear in an actual cube.
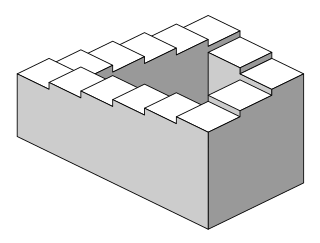
The Penrose stairs or Penrose steps, also dubbed the impossible staircase, is an impossible object created by Oscar Reutersvärd in 1937 and later independently discovered and made popular by Lionel Penrose and his son Roger Penrose. A variation on the Penrose triangle, it is a two-dimensional depiction of a staircase in which the stairs make four 90-degree turns as they ascend or descend yet form a continuous loop, so that a person could climb them forever and never get any higher. This is clearly impossible in three-dimensional Euclidean geometry but possible in some non-Euclidean geometry like in nil geometry.
In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing.
Waterfall is a lithograph by the Dutch artist M. C. Escher, first printed in October 1961. It shows a perpetual motion machine where water from the base of a waterfall appears to run downhill along the water path before reaching the top of the waterfall.
Oscar Reutersvärd was a Swedish graphic artist, who in 1934 pioneered the art of 3D drawings that may initially appear feasible, yet cannot be physically constructed. He is sometimes described as "the father of the impossible figure", although there are much older examples, e.g. Hogarth's Satire on False Perspective.
Anamorphosis is a distorted projection that requires the viewer to occupy a specific vantage point, use special devices, or both to view a recognizable image. It is used in painting, photography, sculpture and installation, toys, and film special effects. The word is derived from the Greek prefix ana-, meaning "back" or "again", and the word morphe, meaning "shape" or "form". Extreme anamorphosis has been used by artists to disguise caricatures, erotic and scatological scenes, and other furtive images from a casual spectator, while revealing an undistorted image to the knowledgeable viewer.
In three-dimensional geometry, a parallel projection is a projection of an object in three-dimensional space onto a fixed plane, known as the projection plane or image plane, where the rays, known as lines of sight or projection lines, are parallel to each other. It is a basic tool in descriptive geometry. The projection is called orthographic if the rays are perpendicular (orthogonal) to the image plane, and oblique or skew if they are not.
In geometry, the rhombille tiling, also known as tumbling blocks, reversible cubes, or the dice lattice, is a tessellation of identical 60° rhombi on the Euclidean plane. Each rhombus has two 60° and two 120° angles; rhombi with this shape are sometimes also called diamonds. Sets of three rhombi meet at their 120° angles, and sets of six rhombi meet at their 60° angles.
Roger Newland Shepard was an American cognitive scientist and author of the "universal law of generalization" (1987). He was considered a father of research on spatial relations. He studied mental rotation, and was an inventor of non-metric multidimensional scaling, a method for representing certain kinds of statistical data in a graphical form that can be comprehended by humans. The optical illusion called Shepard tables and the auditory illusion called Shepard tones are named for him.
Ascending and Descending is a lithograph print by the Dutch artist M. C. Escher first printed in March 1960. The original print measures 14 in × 11+1⁄4 in. The lithograph depicts a large building roofed by a never-ending staircase. Two lines of identically dressed men appear on the staircase, one line ascending while the other descends. Two figures sit apart from the people on the endless staircase: one in a secluded courtyard, the other on a lower set of stairs. While most two-dimensional artists use relative proportions to create an illusion of depth, Escher here and elsewhere uses conflicting proportions to create the visual paradox.
Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.
Geometrical–optical are visual illusions, also optical illusions, in which the geometrical properties of what is seen differ from those of the corresponding objects in the visual field.
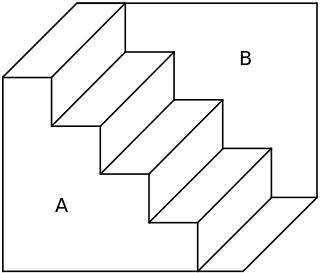
Schroeder stairs is an optical illusion which is a two-dimensional drawing which may be perceived either as a drawing of a staircase leading from left to right downwards or the same staircase only turned upside down, a classical example of perspective reversal in psychology of perception. It is named after the German natural scientist Heinrich G. F. Schröder, who published it in 1858.
The Shepard elephant, also known as L'egs-istential Quandary or the impossible elephant is an optical illusion, of the type impossible object, based on figure-ground confusion. As its creator Roger Shepard explains:
The elephant…belongs to a class of objects that are truly impossible in that the object itself cannot be globally segregated from the nonobject or background. Parts of the object become the background, and vice versa.
Borromean rings — although conventionally drawn as three linked circles in three-dimensional space, any realization must be non-circular. [3]
Penrose stairs – created by Oscar Reutersvärd and later independently devised and popularised by Lionel Penrose and his mathematician son Roger Penrose. [4] A variation on the Penrose triangle, it is a two-dimensional depiction of a staircase in which the stairs make four 90-degree turns as they ascend or descend yet form a continuous loop, so that a person could climb them forever and never get any higher.
Penrose triangle (tribar) – first created by the Swedish artist Oscar Reutersvärd in 1934. Roger Penrose independently devised and popularised it in the 1950s, describing it as "impossibility in its purest form".
Impossible trident (or devil's tuning fork) – also known as a "blivet", this has three cylindrical prongs at one end, which then mysteriously transform into two rectangular prongs at the other end. [5]
Oscar Reutersvärd's optical illusion (1934)
