
In geometry and algebra, a real number is constructible if and only if, given a line segment of unit length, a line segment of length can be constructed with compass and straightedge in a finite number of steps. Equivalently, is constructible if and only if there is a closed-form expression for using only integers and the operations for addition, subtraction, multiplication, division, and square roots.
In mathematics, a polynomial is an expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example with three indeterminates is x3 + 2xyz2 − yz + 1.
In algebra, a quadratic equation is any equation that can be rearranged in standard form as
The fundamental theorem of algebra, also known as d'Alembert's theorem, or the d'Alembert–Gauss theorem, states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This includes polynomials with real coefficients, since every real number is a complex number with its imaginary part equal to zero.
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.
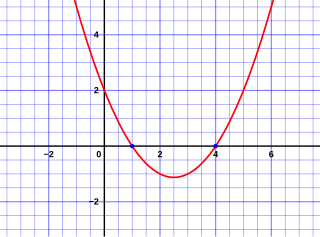
In elementary algebra, the quadratic formula is a formula that provides the two solutions, or roots, to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as completing the square.

In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind. For example, 3 × 5 is an integer factorization of 15, and (x – 2)(x + 2) is a polynomial factorization of x2 – 4.

Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a compass.
In mathematics and computing, a root-finding algorithm is an algorithm for finding zeros, also called "roots", of continuous functions. A zero of a function f, from the real numbers to real numbers or from the complex numbers to the complex numbers, is a number x such that f(x) = 0. As, generally, the zeros of a function cannot be computed exactly nor expressed in closed form, root-finding algorithms provide approximations to zeros, expressed either as floating-point numbers or as small isolating intervals, or disks for complex roots (an interval or disk output being equivalent to an approximate output together with an error bound).

In algebra, a cubic equation in one variable is an equation of the form

In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before the 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic".

In algebra, a quartic function is a function of the form
In mathematics, an algebraic equation or polynomial equation is an equation of the form , where P is a polynomial with coefficients in some field, often the field of the rational numbers. For example, is an algebraic equation with integer coefficients and
In numerical analysis, Bairstow's method is an efficient algorithm for finding the roots of a real polynomial of arbitrary degree. The algorithm first appeared in the appendix of the 1920 book Applied Aerodynamics by Leonard Bairstow. The algorithm finds the roots in complex conjugate pairs using only real arithmetic.
In mathematics, a quadratic equation is a polynomial equation of the second degree. The general form is
In mathematics, a univariate polynomial of degree n with real or complex coefficients has n complex roots, if counted with their multiplicities. They form a multiset of n points in the complex plane. This article concerns the geometry of these points, that is the information about their localization in the complex plane that can be deduced from the degree and the coefficients of the polynomial.
The Jenkins–Traub algorithm for polynomial zeros is a fast globally convergent iterative polynomial root-finding method published in 1970 by Michael A. Jenkins and Joseph F. Traub. They gave two variants, one for general polynomials with complex coefficients, commonly known as the "CPOLY" algorithm, and a more complicated variant for the special case of polynomials with real coefficients, commonly known as the "RPOLY" algorithm. The latter is "practically a standard in black-box polynomial root-finders".

In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being incommensurable, meaning that they share no "measure" in common, that is, there is no length, no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself.
In mathematics, a Carlyle circle is a certain circle in a coordinate plane associated with a quadratic equation; it is named after Thomas Carlyle. The circle has the property that the solutions of the quadratic equation are the horizontal coordinates of the intersections of the circle with the horizontal axis. Carlyle circles have been used to develop ruler-and-compass constructions of regular polygons.
Finding polynomial roots is a long-standing problem that has been the object of much research throughout history. A testament to this is that up until the 19th century, algebra meant essentially theory of polynomial equations.

![Finding roots -1/2, -1/[?]2, and 1/[?]2 of the cubic 4x +2x -2x-1 showing how negative coefficients and extended segments are handled. Each number shown on a colored line is the negative of its slope and hence a real root of the polynomial. LillsMethod.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/9/97/LillsMethod.svg/250px-LillsMethod.svg.png)














