
A tailplane, also known as a horizontal stabiliser, is a small lifting surface located on the tail (empennage) behind the main lifting surfaces of a fixed-wing aircraft as well as other non-fixed-wing aircraft such as helicopters and gyroplanes. Not all fixed-wing aircraft have tailplanes. Canards, tailless and flying wing aircraft have no separate tailplane, while in V-tail aircraft the vertical stabiliser, rudder, and the tail-plane and elevator are combined to form two diagonal surfaces in a V layout.

In fluid dynamics, a stall is a reduction in the lift coefficient generated by a foil as angle of attack increases. This occurs when the critical angle of attack of the foil is exceeded. The critical angle of attack is typically about 15°, but it may vary significantly depending on the fluid, foil, and Reynolds number.
The center of pressure is the point where the total sum of a pressure field acts on a body, causing a force to act through that point. The total force vector acting at the center of pressure is the value of the integrated vectorial pressure field. The resultant force and center of pressure location produce equivalent force and moment on the body as the original pressure field. Pressure fields occur in both static and dynamic fluid mechanics. Specification of the center of pressure, the reference point from which the center of pressure is referenced, and the associated force vector allows the moment generated about any point to be computed by a translation from the reference point to the desired new point. It is common for the center of pressure to be located on the body, but in fluid flows it is possible for the pressure field to exert a moment on the body of such magnitude that the center of pressure is located outside the body.

Flight dynamics is the science of air vehicle orientation and control in three dimensions. The three critical flight dynamics parameters are the angles of rotation in three dimensions about the vehicle's center of gravity (cg), known as pitch, roll and yaw.

An airfoil or aerofoil is the cross-sectional shape of an object whose motion through a gas is capable of generating significant lift, such as a wing, a sail, or the blades of propeller, rotor, or turbine.

In aeronautics, dihedral is the angle between the left and right wings of an aircraft. "Dihedral" is also used to describe the effect of sideslip on the rolling of the aircraft.

A stabilator, more frequently all-moving tail or all-flying tail, is a fully movable aircraft stabilizer. It serves the usual functions of longitudinal stability, control and stick force requirements otherwise performed by the separate parts of a conventional horizontal stabilizer and elevator. Apart from a higher efficiency at high Mach number, it is a useful device for changing the aircraft balance within wide limits, and for mastering the stick forces.
Aircraft flight mechanics are relevant to fixed wing and rotary wing (helicopters) aircraft. An aeroplane, is defined in ICAO Document 9110 as, "a power-driven heavier than air aircraft, deriving its lift chiefly from aerodynamic reactions on surface which remain fixed under given conditions of flight".

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.

A vertical stabilizer or tail fin is the static part of the vertical tail of an aircraft. The term is commonly applied to the assembly of both this fixed surface and one or more movable rudders hinged to it. Their role is to provide control, stability and trim in yaw. It is part of the aircraft empennage, specifically of its stabilizers.

An aircraft stabilizer is an aerodynamic surface, typically including one or more movable control surfaces, that provides longitudinal (pitch) and/or directional (yaw) stability and control. A stabilizer can feature a fixed or adjustable structure on which any movable control surfaces are hinged, or it can itself be a fully movable surface such as a stabilator. Depending on the context, "stabilizer" may sometimes describe only the front part of the overall surface.
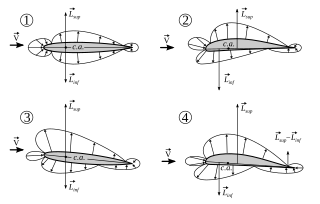
The torques or moments acting on an airfoil moving through a fluid can be accounted for by the net lift and net drag applied at some point on the airfoil, and a separate net pitching moment about that point whose magnitude varies with the choice of where the lift is chosen to be applied. The aerodynamic center is the point at which the pitching moment coefficient for the airfoil does not vary with lift coefficient, making analysis simpler.

In aerodynamics, the pitching moment on an airfoil is the moment produced by the aerodynamic force on the airfoil if that aerodynamic force is considered to be applied, not at the center of pressure, but at the aerodynamic center of the airfoil. The pitching moment on the wing of an airplane is part of the total moment that must be balanced using the lift on the horizontal stabilizer. More generally, a pitching moment is any moment acting on the pitch axis of a moving body.

Stability derivatives, and also control derivatives, are measures of how particular forces and moments on an aircraft change as other parameters related to stability change. For a defined "trim" flight condition, changes and oscillations occur in these parameters. Equations of motion are used to analyze these changes and oscillations. Stability and control derivatives are used to linearize (simplify) these equations of motion so the stability of the vehicle can be more readily analyzed.

In aeronautics, a canard is an arrangement wherein a small forewing or foreplane is placed forward of the main wing of a fixed-wing aircraft or a weapon. The term "canard" may be used to describe the aircraft itself, the wing configuration, or the foreplane. Canard wings are also extensively used in guided missiles and smart bombs.
If an aircraft in flight suffers a disturbance in pitch that causes an increase in angle of attack, it is desirable that the aerodynamic forces on the aircraft cause a decrease in angle of attack so that the disturbance does not cause a continuous increase in angle of attack. This is longitudinal static stability.

A tailless aircraft has no other horizontal aerodynamic surface besides its main wing. It may still have a fuselage, vertical tail fin and/or vertical rudder.
Flight dynamics in aviation and spacecraft, is the study of the performance, stability, and control of vehicles flying through the air or in outer space. It is concerned with how forces acting on the vehicle determine its velocity and attitude with respect to time.

Steady flight, unaccelerated flight, or equilibrium flight is a special case in flight dynamics where the aircraft's linear and angular velocity are constant in a body-fixed reference frame. Basic aircraft maneuvers such as level flight, climbs and descents, and coordinated turns can be modeled as steady flight maneuvers. Typical aircraft flight consists of a series of steady flight maneuvers connected by brief, accelerated transitions. Because of this, primary applications of steady flight models include aircraft design, assessment of aircraft performance, flight planning, and using steady flight states as the equilibrium conditions around which flight dynamics equations are expanded.

The dynamic stall is one of the hazardous phenomena on helicopter rotors, which can cause the onset of large torsional airloads and vibrations on the rotor blades. Unlike fixed-wing aircraft, of which the stall occurs at relatively low flight speed, the dynamic stall on a helicopter rotor emerges at high airspeeds or/and during manoeuvres with high load factors of helicopters, when the angle of attack(AOA) of blade elements varies intensively due to time-dependent blade flapping, cyclic pitch and wake inflow. For example, during forward flight at the velocity close to VNE, velocity, never exceed, the advancing and retreating blades almost reach their operation limits whereas flows are still attached to the blade surfaces. That is, the advancing blades operate at high Mach numbers so low values of AOA is needed but shock-induced flow separation may happen, while the retreating blade operates at much lower Mach numbers but the high values of AoA result in the stall.

















































