
In theoretical physics, a Feynman diagram is a pictorial representation of the mathematical expressions describing the behavior and interaction of subatomic particles. The scheme is named after American physicist Richard Feynman, who introduced the diagrams in 1948. The interaction of subatomic particles can be complex and difficult to understand; Feynman diagrams give a simple visualization of what would otherwise be an arcane and abstract formula. According to David Kaiser, "Since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations. Feynman diagrams have revolutionized nearly every aspect of theoretical physics." While the diagrams are applied primarily to quantum field theory, they can also be used in other fields, such as solid-state theory. Frank Wilczek wrote that the calculations which won him the 2004 Nobel Prize in Physics "would have been literally unthinkable without Feynman diagrams, as would [Wilczek's] calculations that established a route to production and observation of the Higgs particle."
In physical chemistry, the Arrhenius equation is a formula for the temperature dependence of reaction rates. The equation was proposed by Svante Arrhenius in 1889, based on the work of Dutch chemist Jacobus Henricus van 't Hoff who had noted in 1884 that the van 't Hoff equation for the temperature dependence of equilibrium constants suggests such a formula for the rates of both forward and reverse reactions. This equation has a vast and important application in determining rate of chemical reactions and for calculation of energy of activation. Arrhenius provided a physical justification and interpretation for the formula. Currently, it is best seen as an empirical relationship. It can be used to model the temperature variation of diffusion coefficients, population of crystal vacancies, creep rates, and many other thermally-induced processes/reactions. The Eyring equation, developed in 1935, also expresses the relationship between rate and energy.

The reaction rate or rate of reaction is the speed at which a chemical reaction takes place, defined as proportional to the increase in the concentration of a product per unit time and to the decrease in the concentration of a reactant per unit time. Reaction rates can vary dramatically. For example, the oxidative rusting of iron under Earth's atmosphere is a slow reaction that can take many years, but the combustion of cellulose in a fire is a reaction that takes place in fractions of a second. For most reactions, the rate decreases as the reaction proceeds. A reaction's rate can be determined by measuring the changes in concentration over time.
In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. The terms "distribution" and "family" are often used loosely: specifically, an exponential family is a set of distributions, where the specific distribution varies with the parameter; however, a parametric family of distributions is often referred to as "a distribution", and the set of all exponential families is sometimes loosely referred to as "the" exponential family. They are distinct because they possess a variety of desirable properties, most importantly the existence of a sufficient statistic.

Collision theory states that when suitable particles of the reactant hit each other with correct orientation, only a certain amount of collisions result in a perceptible or notable change; these successful changes are called successful collisions. The successful collisions must have enough energy, also known as activation energy, at the moment of impact to break the pre-existing bonds and form all new bonds. This results in the products of the reaction. Increasing the concentration of the reactant brings about more collisions and hence more successful collisions. Increasing the temperature increases the average kinetic energy of the molecules in a solution, increasing the amount of collisions that have enough energy. Collision theory was proposed independently by Max Trautz in 1916 and William Lewis in 1918.

In probability theory and statistics, the generalized inverse Gaussian distribution (GIG) is a three-parameter family of continuous probability distributions with probability density function

A premixed flame is a flame formed under certain conditions during the combustion of a premixed charge of fuel and oxidiser. Since the fuel and oxidiser—the key chemical reactants of combustion—are available throughout a homogeneous stoichiometric premixed charge, the combustion process once initiated sustains itself by way of its own heat release. The majority of the chemical transformation in such a combustion process occurs primarily in a thin interfacial region which separates the unburned and the burned gases. The premixed flame interface propagates through the mixture until the entire charge is depleted. The propagation speed of a premixed flame is known as the flame speed which depends on the convection-diffusion-reaction balance within the flame, i.e. on its inner chemical structure. The premixed flame is characterised as laminar or turbulent depending on the velocity distribution in the unburned pre-mixture.
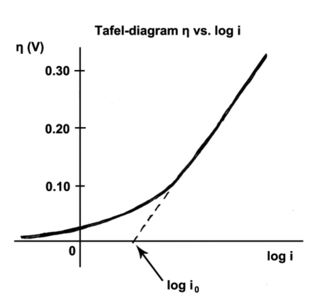
The Tafel equation is an equation in electrochemical kinetics relating the rate of an electrochemical reaction to the overpotential. The Tafel equation was first deduced experimentally and was later shown to have a theoretical justification. The equation is named after Swiss chemist Julius Tafel.
" It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction ".

Transition state theory (TST) explains the reaction rates of elementary chemical reactions. The theory assumes a special type of chemical equilibrium (quasi-equilibrium) between reactants and activated transition state complexes.
In chemical kinetics, an Arrhenius plot displays the logarithm of a reaction rate constant, (, ordinate axis) plotted against reciprocal of the temperature (, abscissa). Arrhenius plots are often used to analyze the effect of temperature on the rates of chemical reactions. For a single rate-limited thermally activated process, an Arrhenius plot gives a straight line, from which the activation energy and the pre-exponential factor can both be determined.
Diffusion-controlled reactions are reactions in which the reaction rate is equal to the rate of transport of the reactants through the reaction medium. The process of chemical reaction can be considered as involving the diffusion of reactants until they encounter each other in the right stoichiometry and form an activated complex which can form the product species. The observed rate of chemical reactions is, generally speaking, the rate of the slowest or "rate determining" step. In diffusion controlled reactions the formation of products from the activated complex is much faster than the diffusion of reactants and thus the rate is governed by collision frequency.

Spinodal decomposition is a mechanism by which a single thermodynamic phase spontaneously separates into two phases. Decomposition occurs when there is no thermodynamic barrier to phase separation. As a result, phase separation via decomposition does not require the nucleation events resulting from thermodynamic fluctuations which normally trigger phase separation.
In electrochemistry, the Butler–Volmer equation, also known as Erdey-Grúz–Volmer equation, is one of the most fundamental relationships in electrochemical kinetics. It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction, considering that both a cathodic and an anodic reaction occur on the same electrode:
Common integrals in quantum field theory are all variations and generalizations of Gaussian integrals to the complex plane and to multiple dimensions. Other integrals can be approximated by versions of the Gaussian integral. Fourier integrals are also considered.
In physical chemistry, there are numerous quantities associated with chemical compounds and reactions; notably in terms of amounts of substance, activity or concentration of a substance, and the rate of reaction. This article uses SI units.
The eddy break-up model (EBU) is used in combustion engineering. Combustion modeling has a wide range of applications. In most of the combustion systems, fuel and oxygen are separately supplied in the combustion chamber. Due to this, chemical reaction and combustion occur simultaneously in the combustion chamber. However, the rate of the chemical reaction is faster than the rate of mixing fuel and oxygen. Therefore, that rate of combustion is controlled by rate of mixing. Such cases, where formation of pre-mixture is difficult, are called diffusion combustion or diffusion flames.

A polymer is a macromolecule, composed of many similar or identical repeated subunits. Polymers are common in, but not limited to, organic media. They range from familiar synthetic plastics to natural biopolymers such as DNA and proteins. Their unique elongated molecular structure produces unique physical properties, including toughness, viscoelasticity, and a tendency to form glasses and semicrystalline structures. The modern concept of polymers as covalently bonded macromolecular structures was proposed in 1920 by Hermann Staudinger. One sub-field in the study of polymers is polymer physics. As a part of soft matter studies, Polymer physics concerns itself with the study of mechanical properties and focuses on the perspective of condensed matter physics.
Chemical reaction models transform physical knowledge into a mathematical formulation that can be utilized in computational simulation of practical problems in chemical engineering. Computer simulation provides the flexibility to study chemical processes under a wide range of conditions. Modeling of a chemical reaction involves solving conservation equations describing convection, diffusion, and reaction source for each component species.
In combustion, Frank-Kamenetskii theory explains the thermal explosion of a homogeneous mixture of reactants, kept inside a closed vessel with constant temperature walls. It is named after a Russian scientist David A. Frank-Kamenetskii, who along with Nikolay Semenov developed the theory in the 1930s.
The shear viscosity of a fluid is a material property that describes the friction between internal neighboring fluid surfaces flowing with different fluid velocities. This friction is the effect of (linear) momentum exchange caused by molecules with sufficient energy to move between these fluid sheets due to fluctuations in their motion. The viscosity is not a material constant, but a material property that depends on temperature, pressure, fluid mixture composition, local velocity variations. This functional relationship is described by a mathematical viscosity model called a constitutive equation which is usually far more complex than the defining equation of shear viscosity. One such complicating feature is the relation between the viscosity model for a pure fluid and the model for a fluid mixture which is called mixing rules. When scientists and engineers use new arguments or theories to develop a new viscosity model, instead of improving the reigning model, it may lead to the first model in a new class of models. This article will display one or two representative models for different classes of viscosity models, and these classes are:
Magnussen, B. F., and B. H. Hjertager, “On Mathematical Mod- els of Turbulent Combustion with Special Emphasis on Soot For- mation and Combustion,” Proc. 16th Int. Symp. on Combustion, The Combustion Institute, Pittsburgh, PA (1976).






















