Resonating amplifiers

Any mechanical body that is not infinitely rigid (infinite damping) can exhibit vibration upon experiencing an external forcing. Most vibrating elements can be represented by a second order mass-spring-damper system governed by the following second order differential equation.
where, x is the displacement, m is the effective mass, c is the damping coefficient, k is the spring constant of the restoring force, and F(t) is external forcing as a function of time.
"A mechanical amplifier is basically a mechanical resonator that resonates at the operating frequency and magnifies the amplitude of the vibration of the transducer at anti-node location." [6]
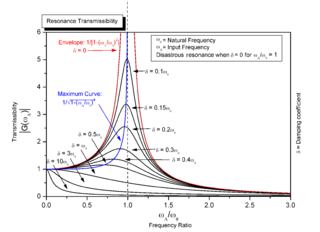
Resonance is the physical phenomenon where the amplitude of oscillation (output) exhibit a buildup over time when the frequency of the external forcing (input) is in the vicinity of a resonant frequency. The output thus achieved is generally larger than the input in terms of displacement, velocity or acceleration. Although resonant frequency is generally used synonymously with natural frequency, there is in fact a distinction. While resonance can be achieved at the natural frequency, it can also be achieved at several other modes such as flexural modes. Therefore, the term resonant frequency encompasses all frequency bandwidths where some forms of resonance can be achieved; and this includes the natural frequency.
Direct resonators

All mechanical vibrating systems possess a natural frequency fn, which is presented as the following in its most basic form.
When an external forcing is applied directly (parallel to the plane of the oscillatory displacement) to the system around the frequency of its natural frequency, then the fundamental mode of resonance can be achieved. The oscillatory amplitude outside this frequency region is typically smaller than the resonant peak and the input amplitude. The amplitude of the resonant peak and the bandwidth of resonance is dependent on the damping conditions and is quantified by the dimensionless quantity Q factor. Higher resonant modes and resonant modes at different planes (transverse, lateral, rotational and flexural) are usually triggered at higher frequencies. The specific frequency vicinity of these modes depends on the nature and boundary conditions of each mechanical system. Additionally, subharmonics, superharmonics or subsuperharmonics of each mode can also be excited at the right boundary conditions. [7]
“As a model for a detector we note that if you hang a weight on a spring and then move the upper end of the spring up and down, the amplitude of the weight will be much larger than the driving amplitude if you are at the resonant frequency of the mass and spring assembly. It is essentially a mechanical amplifier and serves as a good candidate for a sensitive detector." [8]
Parametric resonators
Parametric resonance is the physical phenomenon where an external excitation, at a specific frequency and typically orthogonal to the plane of displacement, introduces a periodic modulation in one of the system parameters resulting in a buildup in oscillatory amplitude. It is governed by the Mathieu equation. The following is a damped Mathieu equation.
where δ is the squared of the natural frequency and ε is the amplitude of the parametric excitation.

The first order or the principal parametric resonance is achieved when the driving/excitation frequency is twice the natural frequency of a given system. Higher orders of parametric resonance are observed either at or at submultiples of the natural frequency. For direct resonance, the response frequency always matches the excitation frequency. However, regardless of which order of parametric resonance is activated, the response frequency of parametric resonance is always in the vicinity of the natural frequency. [9] Parametric resonance has the ability to exhibit higher mechanical amplification than direct resonance when operating at favourable conditions, but usually has a longer build up/transient state. [10]
“The parametric resonator provides a very useful instrument that has been developed by a number of researchers, in part because a parametric resonator can serve as a mechanical amplifier, over a narrow band of frequencies.” [11]
Swing analogy
Direct resonance can be equated to someone pushing a child on a swing. If the frequency of the pushing (external forcing) matches the natural frequency of the child-swing system, direct resonance can be achieved. Parametric resonance, on the other hand, is the child shifting his/her own weight with time (twice the frequency of the natural frequency) and building up the oscillatory amplitude of the swing without anyone helping to push. In other words, there is an internal transfer of energy (instead of simply dissipating all available energy) as the system parameter (child's weight) modulates and changes with time.
Other resonators/oscillators
Other means of signal enhancement, applicable to both mechanical and electrical domains, exist. This include chaos theory, stochastic resonance and many other nonlinear or vibrational phenomena. No new energy is created. However, through mechanical amplification, more of the available power spectrum can be utilised at a more optimal efficiency rather than dissipated.