
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, which gives an equal perceived step size as pitch is perceived roughly as the logarithm of frequency.

Meantone temperament is a musical temperament, that is a tuning system, obtained by slightly compromising the fifths in order to improve the thirds. Meantone temperaments are constructed the same way as Pythagorean tuning, as a stack of equal fifths, but in meantone each fifth is narrow compared to the perfect fifth of ratio 3:2.
In music theory, an interval is the difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.

In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so.

In music theory, the circle of fifths is the relationship among the 12 tones of the chromatic scale, their corresponding key signatures, and the associated major and minor keys. More specifically, it is a geometrical representation of relationships among the 12 pitch classes of the chromatic scale in pitch class space.

In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart, e.g., the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave position." Important to musical set theory, a pitch class is, "all pitches related to each other by octave, enharmonic equivalence, or both." Thus, using scientific pitch notation, the pitch class "C" is the set

Regular temperament is any tempered system of musical tuning such that each frequency ratio is obtainable as a product of powers of a finite number of generators, or generating frequency ratios. For instance, in 12-TET, the system of music most commonly used in the Western world, the generator is a tempered fifth, which is the basis behind the circle of fifths.

In music theory, pitch spaces model relationships between pitches. These models typically use distance to model the degree of relatedness, with closely related pitches placed near one another, and less closely related pitches placed farther apart. Depending on the complexity of the relationships under consideration, the models may be multidimensional. Models of pitch space are often graphs, groups, lattices, or geometrical figures such as helixes. Pitch spaces distinguish octave-related pitches. When octave-related pitches are not distinguished, we have instead pitch class spaces, which represent relationships between pitch classes. Chordal spaces model relationships between chords.

Scientific pitch notation is a method of specifying musical pitch by combining a musical note name and a number identifying the pitch's octave.

In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.
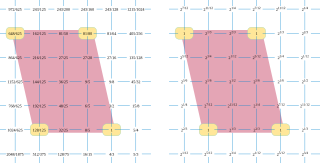
Fokker periodicity blocks are a concept in tuning theory used to mathematically relate musical intervals in just intonation to those in equal tuning. They are named after Adriaan Daniël Fokker. These are included as the primary subset of what Erv Wilson refers to as constant structures, where "each interval occurs always subtended by the same number of steps".
In music, septimal meantone temperament, also called standard septimal meantone or simply septimal meantone, refers to the tempering of 7-limit musical intervals by a meantone temperament tuning in the range from fifths flattened by the amount of fifths for 12 equal temperament to those as flat as 19 equal temperament, with 31 equal temperament being a more or less optimal tuning for both the 5- and 7-limits. Meantone temperament represents a frequency ratio of approximately 5 by means of four fifths, so that the major third, for instance C-E, is obtained from two tones in succession. Septimal meantone represents the frequency ratio of 56 (7*23) by ten fifths, so that the interval 7:4 is reached by five successive tones. Hence C-A♯, not C-B♭, represents a 7:4 interval in septimal meantone.

In music theory, pitch-class space is the circular space representing all the notes in a musical octave. In this space, there is no distinction between tones that are separated by an integral number of octaves. For example, C4, C5, and C6, though different pitches, are represented by the same point in pitch class space.
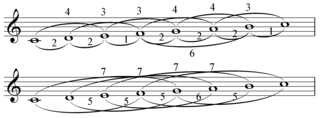
In diatonic set theory, Rothenberg propriety is an important concept, lack of contradiction and ambiguity, in the general theory of musical scales which was introduced by David Rothenberg in a seminal series of papers in 1978. The concept was independently discovered in a more restricted context by Gerald Balzano, who termed it coherence.

Music theory has no axiomatic foundation in modern mathematics, although some interesting work has recently been done in this direction, yet the basis of musical sound can be described mathematically and exhibits "a remarkable array of number properties". Elements of music such as its form, rhythm and metre, the pitches of its notes and the tempo of its pulse can be related to the measurement of time and frequency, offering ready analogies in geometry.

Generalized keyboards are musical keyboards, a type of isomorphic keyboard, with regular, tile-like arrangements usually with rectangular or hexagonal keys, and were developed for performing music in different tunings. They were introduced by Robert Bosanquet in the 1870s, and since the 1960s Erv Wilson has developed new methods of using and expanding them, proposing keyboard layouts including any scale made of a single generator within an "octave" of any size.
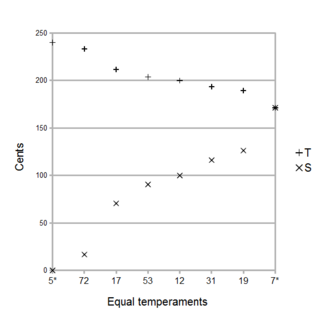
A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's. In such a tuning, then the notes are connected together in a chain of seven fifths, all the same size which makes it a Linear temperament with the tempered fifth as a generator.
Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as 2−3·31·51 = 15/8.

In musical tuning, a lattice "is a way of modeling the tuning relationships of a just intonation system. It is an array of points in a periodic multidimensional pattern. Each point on the lattice corresponds to a ratio. The lattice can be two-, three-, or n-dimensional, with each dimension corresponding to a different prime-number partial [pitch class]." When listed in a spreadsheet a lattice may be referred to as a tuning table.


















