In music theory, limits or harmonic limits are a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term limit was introduced by Harry Partch, [1] who used it to give an upper bound on the complexity of harmony; hence the name.
Harry Partch, Ivor Darreg, and Ralph David Hill are among the many microtonalists to suggest that music has been slowly evolving to employ higher and higher harmonics in its constructs (see emancipation of the dissonance).[ citation needed ] In medieval music, only chords made of octaves and perfect fifths (involving relationships among the first three harmonics) were considered consonant. In the West, triadic harmony arose (contenance angloise) around the time of the Renaissance, and triads quickly became the fundamental building blocks of Western music. The major and minor thirds of these triads invoke relationships among the first five harmonics.
Around the turn of the 20th century, tetrads debuted as fundamental building blocks in African-American music.[ citation needed ] In conventional music theory pedagogy, these seventh chords are usually explained as chains of major and minor thirds. However, they can also be explained as coming directly from harmonics greater than 5. For example, the dominant seventh chord in 12-ET approximates 4:5:6:7, while the major seventh chord approximates 8:10:12:15.
In just intonation, intervals between pitches are drawn from the rational numbers. Since Partch, two distinct formulations of the limit concept have emerged: odd limit and prime limit. Odd limit and prime limit n do not include the same intervals even when n is an odd prime.
For a positive odd number n, the n-odd-limit contains all rational numbers such that the largest odd number that divides either the numerator or denominator is not greater than n.
In Genesis of a Music , Harry Partch considered just intonation rationals according to the size of their numerators and denominators, modulo octaves. [2] Since octaves correspond to factors of 2, the complexity of any interval may be measured simply by the largest odd factor in its ratio. Partch's theoretical prediction of the sensory dissonance of intervals (his "One-Footed Bride") are very similar to those of theorists including Hermann von Helmholtz, William Sethares, and Paul Erlich. [3]
See § Examples, below.
An identity is each of the odd numbers below and including the (odd) limit in a tuning. For example, the identities included in 5-limit tuning are 1, 3, and 5. Each odd number represents a new pitch in the harmonic series and may thus be considered an identity:
C C G C E G B C D E F G ... 1 2 3 4 5 6 7 8 9 10 11 12 ...
According to Partch: "The number 9, though not a prime, is nevertheless an identity in music, simply because it is an odd number." [4] Partch defines "identity" as "one of the correlatives, 'major' or 'minor', in a tonality; one of the odd-number ingredients, one or several or all of which act as a pole of tonality". [5]
Odentity and udentity are short for over-identity and under-identity, respectively. [6] According to music software producer Tonalsoft: "An udentity is an identity of an utonality". [7]
For a prime number n, the n-prime-limit contains all rational numbers that can be factored using primes no greater than n. In other words, it is the set of rationals with numerator and denominator both n-smooth.
p-Limit Tuning. Given a prime number p, the subset of consisting of those rational numbers x whose prime factorization has the form with forms a subgroup of (). ... We say that a scale or system of tuning uses p-limit tuning if all interval ratios between pitches lie in this subgroup. [8]
In the late 1970s, a new genre of music began to take shape on the West coast of the United States, known as the American gamelan school. Inspired by Indonesian gamelan, musicians in California and elsewhere began to build their own gamelan instruments, often tuning them in just intonation. The central figure of this movement was the American composer Lou Harrison [ citation needed ]. Unlike Partch, who often took scales directly from the harmonic series, the composers of the American Gamelan movement tended to draw scales from the just intonation lattice, in a manner like that used to construct Fokker periodicity blocks. Such scales often contain ratios with very large numbers, that are nevertheless related by simple intervals to other notes in the scale.
Prime-limit tuning and intervals are often referred to using the term for the numeral system based on the limit. For example, 7-limit tuning and intervals are called septimal, 11-limit is called undecimal, and so on.
| ratio | interval | odd-limit | prime-limit | audio |
|---|---|---|---|---|
| 3/2 | perfect fifth | 3 | 3 | ⓘ |
| 4/3 | perfect fourth | 3 | 3 | ⓘ |
| 5/4 | major third | 5 | 5 | ⓘ |
| 5/2 | major tenth | 5 | 5 | ⓘ |
| 5/3 | major sixth | 5 | 5 | ⓘ |
| 7/5 | lesser septimal tritone | 7 | 7 | ⓘ |
| 10/7 | greater septimal tritone | 7 | 7 | ⓘ |
| 9/8 | major second | 9 | 3 | ⓘ |
| 27/16 | Pythagorean major sixth | 27 | 3 | ⓘ |
| 81/64 | ditone | 81 | 3 | ⓘ |
| 243/128 | Pythagorean major seventh | 243 | 3 | ⓘ |
In musical temperament, the simple ratios of just intonation are mapped to nearby irrational approximations. This operation, if successful, does not change the relative harmonic complexity of the different intervals, but it can complicate the use of the harmonic limit concept. Since some chords (such as the diminished seventh chord in 12-ET) have several valid tunings in just intonation, their harmonic limit may be ambiguous.
In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth.
In music theory, the tritone is defined as a musical interval spanning three adjacent whole tones. For instance, the interval from F up to the B above it is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B.
In music theory, a minor seventh is one of two musical intervals that span seven staff positions. It is minor because it is the smaller of the two sevenths, spanning ten semitones. The major seventh spans eleven. For example, the interval from A to G is a minor seventh, as the note G lies ten semitones above A, and there are seven staff positions from A to G. Diminished and augmented sevenths span the same number of staff positions, but consist of a different number of semitones.
In Western music, the adjectives major and minor may describe an interval, chord, scale, or key. A composition, movement, section, or phrase may also be referred to by its key, including whether that key is major or minor.
The 43-tone scale is a just intonation scale with 43 pitches in each octave. It is based on an eleven-limit tonality diamond, similar to the seven-limit diamond previously devised by Max Friedrich Meyer and refined by Harry Partch.
Otonality and utonality are terms introduced by Harry Partch to describe chords whose pitch classes are the harmonics or subharmonics of a given fixed tone (identity), respectively. For example: 1/1, 2/1, 3/1,... or 1/1, 1/2, 1/3,....
An Otonality is that set of pitches generated by the numerical factors (...identities)...over a numerical constant in the denominator. Conversely, a Utonality is the inversion of an Otonality, a set of pitches with a numerical constant in the numerator over the numerical factors...in the denominator.
In music theory and tuning, a tonality diamond is a two-dimensional diagram of ratios in which one dimension is the Otonality and one the Utonality. Thus the n-limit tonality diamond is an arrangement in diamond-shape of the set of rational numbers r, , such that the odd part of both the numerator and the denominator of r, when reduced to lowest terms, is less than or equal to the fixed odd number n. Equivalently, the diamond may be considered as a set of pitch classes, where a pitch class is an equivalence class of pitches under octave equivalence. The tonality diamond is often regarded as comprising the set of consonances of the n-limit. Although originally invented by Max Friedrich Meyer, the tonality diamond is now most associated with Harry Partch.
12 equal temperament (12-ET) is the musical system that divides the octave into 12 parts, all of which are equally tempered on a logarithmic scale, with a ratio equal to the 12th root of 2. That resulting smallest interval, 1⁄12 the width of an octave, is called a semitone or half step.
In number theory, Størmer's theorem, named after Carl Størmer, gives a finite bound on the number of consecutive pairs of smooth numbers that exist, for a given degree of smoothness, and provides a method for finding all such pairs using Pell equations. It follows from the Thue–Siegel–Roth theorem that there are only a finite number of pairs of this type, but Størmer gave a procedure for finding them all.
A septimal comma is a small musical interval in just intonation that contains the number seven in its prime factorization. There is more than one such interval, so the term septimal comma is ambiguous, but it most commonly refers to the interval 64/63.
Music theory analyzes the pitch, timing, and structure of music. It uses mathematics to study elements of music such as tempo, chord progression, form, and meter. The attempt to structure and communicate new ways of composing and hearing music has led to musical applications of set theory, abstract algebra and number theory.
Tonality flux is Harry Partch's term for the kinds of subtle harmonic changes that can occur in a microtonal context from notes moving from one chord to another by tiny increments of voice leading. For instance, within a major third G-B, there can be a minor third G to B, such that in moving from one to the other each line shifts less than a half-step. Within a just intonation scale, this could be represented by
Genesis of a Music is a book first published in 1949 by microtonal composer Harry Partch (1901–1974).
The harmonic seventh interval, also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio (about 969 cents). This is somewhat narrower than and is, "particularly sweet", "sweeter in quality" than an "ordinary" just minor seventh, which has an intonation ratio of 9:5 (about 1018 cents).
Dynamic tonality is a paradigm for tuning and timbre which generalizes the special relationship between just intonation, and the harmonic series to apply to a wider set of pseudo-just tunings and related pseudo-harmonic timbres.
Paul Erlich is a guitarist and music theorist living near Boston, Massachusetts. He is known for his seminal role in developing the theory of regular temperaments, including being the first to define pajara temperament and its decatonic scales in 22-ET. He holds a Bachelor of Science degree in physics from Yale University.
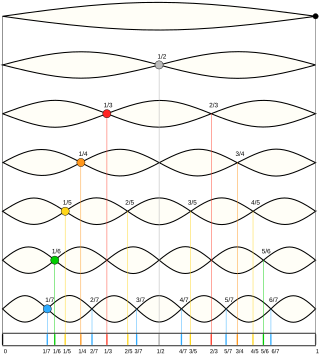
The scale of harmonics is a musical scale based on the noded positions of the natural harmonics existing on a string. This musical scale is present on the guqin, regarded as one of the first string instruments with a musical scale. Most fret positions appearing on Non-Western string instruments (lutes) are equal to positions of this scale. Unexpectedly, these fret positions are actually the corresponding undertones of the overtones from the harmonic series. The distance from the nut to the fret is an integer number lower than the distance from the fret to the bridge.
Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as 2−3·31·51 = 15/8.
7-limit or septimal tunings and intervals are musical instrument tunings that have a limit of seven: the largest prime factor contained in the interval ratios between pitches is seven. Thus, for example, 50:49 is a 7-limit interval, but 14:11 is not.
| Composers |
|   | |||||
|---|---|---|---|---|---|---|---|
| Inventors | |||||||
| Tunings and scales |
| ||||||
| Concepts and techniques | |||||||
| Groups and publications | |||||||
| Compositions | |||||||
| Other topics | |||||||
