Vallotti temperament

Last updated

The circulating temperament today referred to as Vallotti temperament (or simply Vallotti, Vallotti-Barca, Vallotti-Tartini, or Vallotti-Young) is a shifted version of Young's second temperament. Its attribution to the 18th-century organist, composer, and music theorist, Francesco Vallotti is a mistake, since there is no evidence that he ever suggested it. It is however audibly indistinguishable from a slightly different temperament that was in fact devised by Vallotti.

Contents

Vallotti's description of his temperament appears in book 2 of his treatise, Della scienza teorica e pratica della moderna musica (On the theoretical and practical science of modern music). Although he stated that he had developed his theoretical system—presumably including the details of his temperament—by 1728, the first book of his treatise was not published until 1779, the year before he died. At the time of his death, the other three books had not been published, and remained only in manuscript form until an edition of all four books was published in 1950, under the title Trattato della moderna musica (Treatise on modern music). [1]

Vallotti's temperament received very little attention during his lifetime and for some time thereafter. [2] In a treatise published in 1754, [3] Vallotti's friend and colleague Giuseppe Tartini praised the former's approach to temperament, and outlined some of its features, but without giving sufficient detail for the temperament itself to be identified. [4] In 1781, the mathematician William Jones noted Tartini's preference for Vallotti's temperament, and gave a similarly vague and unspecific description. [5]

The temperament originally devised by Vallotti has six fifths tempered by 1⁄6 of a syntonic comma, five perfectly just, and one tempered by a schisma. In a manuscript which remained unpublished until 1987, [6] the Italian chemist and musical theorist, Alessandro Barca, proposed that this latter fifth be sharpened by 5⁄6 of a schisma, and all the pure fifths be flattened by 1⁄6 of a schisma. Barca's version thus has six fifths tempered by 1⁄6 of a syntonic comma, and six tempered by 1⁄6 of a schisma. In the temperament now commonly misattributed to Vallotti, the odd fifth out in his original is sharpened by a full schisma, and each of the six tempered fifths is flattened by a further 1⁄6 of a schisma. This modern version thus has six fifths tempered by 1⁄6 of a Pythagorean comma, and six perfectly just. More recently, the tuning and keyboard construction expert, Owen Jorgensen, has proposed a version of Vallotti's temperament in which the beating frequencies of the tempered fifths, rather than their sizes, are chosen to be equal. In practice, none of these four versions is audibly distinguishable from any of the others, [7] because no interval in any of them differs from the corresponding interval in any of the other three by as much as 2 cents.

Description

In the circulating temperament today commonly misattributed to Vallotti, each of the fifths B-F♯, F♯-C♯, C♯-G♯, G♯-E♭, E♭-B♭, and B♭-F are perfectly just, while the fifths F-C, C-G, G-D, D-A, A-E, and E-B are each 1⁄6 of a Pythagorean (ditonic) comma narrower than just. [8] The exact and approximate numerical sizes of these fifths, in cents, are given by:

f1Def=1200 ( log2(3) − 1) ≈ 701.96(perfectly just)
f2Def=2600 − 1200 log2(3) ≈ 698.04(flatter than just by 1⁄6 of a ditonic comma)

If  sj Def= fj − 600  for j = 1,2, the sizes of the major thirds in this temperament are: [9]

  Major third  F-A, C-E,
G-B		D-F♯,
B♭-D		A-C♯,
E♭-G		E-G♯,
G♯-C		B-E♭, F♯-B♭,
C♯-F
Width
exact
approx.
4 s2
 392.18 		 3 s2 + s1 
396.09		 2 s2 + 2 s1 
400 (exactly)		 s2 + 3 s1 
403.91		 4 s1 
407.82
Deviation
from just		+5.9+9.8+13.7+17.6+21.5

The following table gives the pitch differences in cents between the notes of a chromatic scale tuned with this temperament and those of one tuned with equal temperament, when the note A of each scale is given the same pitch. [10]

Note E♭B♭FCGD A EBF♯C♯G♯
Difference from
equal temperament 		+3.9+5.9+7.8+5.9+3.9+2.00-2.0-3.9-2.00+2.0

This temperament is merely a shifted version of Young's second temperament, which also has six consecutive pure fifths and six tempered by 1⁄6 of a Pythagorean comma. In Young's second temperament, however, the sequence of tempered fifths starts from the note C, rather than from F, as they do in the temperament today commonly misattributed to Vallotti. [11]

Other versions

Vallotti's original

In the original description of his temperament, Vallotti made each of the fifths B-F♯, F♯-C♯, C♯-G♯, G♯-E♭, and E♭-B♭ perfectly just, just as in the modern version, but rather than making the fifths F-C, C-G, G-D, D-A, A-E, and E-B narrower than just by a 1⁄6 of a Pythagorean comma, he had narrowed them by only 1⁄6 of a syntonic comma. This left the remaining fifth, B♭-F, narrower than just by a schisma. [12] The exact and approximate numerical sizes of these latter fifths, in cents, are given by:

f3Def=200 ( 2 log2(3) + log2(5) – 2 ) ≈ 698.37(flatter than just by 1⁄6 of a syntonic comma)
f4Def=1200 ( 14 – 7 log2(3) – log2(5) ) ≈ 700.00(flatter than just by a schisma)

If  s1  is defined as above, and  sj Def= fj − 600  for j = 3,4, the sizes of the major thirds in this temperament are:

  Major third  F-A, C-E,
G-B		D-F♯A-C♯E-G♯B-E♭,
F♯-B♭		C♯-FG♯-CE♭-GB♭-D
Width
exact
approx.
4 s3
 393.48 		 3 s3 + s1 
397.07		 2 s3 + 2 s1 
400.65		 s3 + 3 s1 
404.24		 4 s1 
407.82		s4 + 3 s1 
405.87		 s3 + s4 + 2 s1 
402.28		 2 s3 + s4 + s1 
398.70		 3 s3 + s4
395.11
Deviation
from just		+7.2+10.8+14.3+17.9+21.5+19.6+16.0+12.4+8.8

The following table gives the pitch differences in cents between the notes of a chromatic scale tuned with this temperament and those of one tuned with equal temperament, when the note A of each scale is given the same pitch.

Note E♭B♭FCGD A EBF♯C♯G♯
Difference from
equal temperament 		+4.6+6.5+6.5+4.9+3.3+1.60-1.6-3.3-1.3+0.65+2.6

Barca's suggested modification

In an 18th-century work, which remained unpublished until 1987, Alessandro Barca suggested that the schisma discrepancy which Vallotti had left to fall entirely in the single fifth, B♭-F, be instead spread amongst the six fifths B-F♯, F♯-C♯, C♯-G♯, G♯-E♭, E♭-B♭, and B♭-F, thus making them each narrower than just by the negligible quantity 1⁄6 of a schisma (about 1⁄3 of a cent). The exact and approximate numerical size of these fifths, in cents, is given by:

f5Def=200 ( 9 – 2 log2(3) – log2(5) ) ≈ 701.63(flatter than just by 1⁄6 of a schisma)

If  s3  is defined as above, and  s5 Def= f5 − 600, the sizes of the major thirds in this temperament are:

  Major third  F-A, C-E,
G-B		D-F♯,
B♭-D		A-C♯,
E♭-G		E-G♯,
G♯-C		B-E♭, F♯-B♭,
C♯-F
Width
exact
approx.
4 s3
 393.48 		 3 s3 + s5 
396.74		 2 s3 + 2 s5 
400 (exactly)		 s3 + 3 s5 
403.26		 4 s5 
406.52
Deviation
from just		+7.2+9.5+13.7+17.0+20.2

The following table gives the pitch differences in cents between the notes of a chromatic scale tuned with this temperament and those of one tuned with equal temperament, when the note A of each scale is given the same pitch.

Note E♭B♭FCGD A EBF♯C♯G♯
Difference from
equal temperament 		+3.3+4.9+6.5+4.9+3.3+1.60-1.6-3.3-1.60+1.6

Jorgensen's version with equal-beating fifths

One of the leading experts on keyboard construction and tuning, Owen Jorgensen, contended that tempering fifths by precisely the same amount on keyboards—with the possible exception of the organ—was beyond the capabilities of tuning practices used before the twentieth century, [13] and that the vast majority of keyboard tuners, when tuning by ear before the development of twentieth century tuning techniques, would have judged two adjacent or overlapping fifths to be the same whenever they beat at the same rate. [14]

Jorgensen gave two sets of instructions for tuning Valotti's temperament in a way which he considered representative of what he believed would have been the results achieved by 18th- and 19th-century tuners. The first used a bearing plan for the octave F3 to F4, [15] the second, a bearing plan for the higher octave, F4 to F5. [16] In the first, middle C (C4) is tuned to a standard pitch of 220 4√2 Hz, all octaves, and the fifths B–F♯, F♯–C♯, C♯–G♯, E♭–B♭ and B♭–F are tuned just, while the fifths F3–C4, C3–G3, G3–D4, D3–A3, A3–E4, and E3–B3 are tuned narrow, all with a beat rate of 1.1 Hz. The amounts by which these tempered fifths are narrow range from 2.9 cents for A–E to 4.9 cents for C–G, and average to 3.8 cents, slightly less than a sixth of the Pythagorean comma. As a consequence, the diminished sixth G♯–E♭, which is required to be a perfectly just fifth in Vallotti proper, turns out to be tempered narrow by 0.6 cents in this version of Jorgensen's. The sizes of its major thirds in cents are: [17]

  Major third  F-AC-EG-BD-F♯A-C♯E-G♯B-E♭, F♯-B♭,
C♯-F		G♯-CE♭-GB♭-D
Width
(approx.)
 391.74 392.48393.46396.71401.05403.95407.21403.58399.32396.08
Deviation
from just		+5.4+6.2+7.1+10.4+14.7+17.6+20.9+17.3+13.0+9.8

The following table gives the pitch differences in cents between the notes of a chromatic scale tuned with Jorgensen's equal-beating version of Vallotti temperament and those of one tuned with equal temperament, when the note C4 of each scale is given the same pitch, 220 4√2 Hz. [18]

Note E♭B♭FCGD A EBF♯C♯G♯
Difference from
equal temperament 		-2.2-0.3+1.70-2.9-4.2-6.6-7.5-9.4-7.5-5.5-3.5

Notes

  1. ↑ Damschroder and Williams (1990, p.365); Hansell (2001, 2007).
  2. ↑ Barbieri (1982, pp.63, 65). Barbieri quotes the chemist and musical theorist, Alessandro Barca, writing sometime after Vallotti's death, as saying that his temperament had been little more than merely referred to in his unpublished writings.
  3. ↑ Trattato di musica secondo la vera scienza dell' armonia (Tartini, 1754)
  4. ↑ Tartini (1754, p.100). Benjamin Stillingfleet translates the relevant passage from Tartini's treatise as follows (Stillingfleet, 1771, p.35):
    "and I infinitely applaud the opinion of P. Vallotti, our organ-master, as the most reasonable of all. He says, that you ought to give to the white keys of the organ all their natural perfection –, both because they are the natural notes of the diatonic genus, and because in church-music the greatest use is made of them; throwing thus the greatest imperfection upon those black keys, which are most remote from the diatonic scale, and which are hardly ever used."
    The original Italian reads (Tartini, 1754, p.100):
    "ed io lodo infinitamente il sentimento del Padre Valloti nostro Maestro come il più ragionevole di tutti, perchè il più prudente. Egli, dice, che si deve lasciare a' tasti bianchi dell' organo tutta la loro naturale perfezione; sì perchè sono li naturali del Genere diatonico; sì perchè di quelli nel servigio Ecclesiastico sé ne fa il maggior uso: riducendo la massima imperfezione a que' tasti neri, che fono i più lontani dal Genere diatonico, e di quasi niun' uso."
  5. ↑ Jones (1781, pp.325–326).
  6. ↑ When it was published in Patrizio Barbieri's Acustica accordatura e temperamento nell’Illuminismo veneto. Con scritti inediti di Alessandro Barca, Giordano Riccati e altri autori (Barbieri, 1987).
  7. ↑ Except by carefully timing the beats generated by some non-just intervals.
  8. ↑ Donahue (2005, p.28)
  9. ↑ Jorgensen (1991, Table 51-1, p.180).
  10. ↑ Jorgensen (1991, Table 52-1, p.185).
  11. ↑ Donahue (2005, pp.28–9 )
  12. ↑ Barbieri (1982, p.63); Di Veroli (2013, p.125)
  13. ↑ Jorgensen (1991, pp.44–45, 175, 310–11). Although the only specific temperaments Jorgensen mentions in this connection are 12-tone equal and quarter-comma meantone, his comment on (on p.45) that "[t]wentieth-century acoustic knowledge and test-interval techniques are required for tuning any regular temperament by ear" implies a belief that the same limitation applied to the tempering of fifths precisely by any specified amount.
  14. ↑ Jorgensen (1991, pp.44, 310). Sturm (2011) and Di Veroli (2013, pp.146-48) have dismissed these contentions of Jorgensen's as unfounded speculation.
  15. ↑ Jorgensen (1991, pp.68–73). Notes are specified here using scientific pitch notation. F3 is the highest F below middle C, and F4 is the next above it.
  16. ↑ Jorgensen (1991, pp.176–77).
  17. ↑ Jorgensen (1991, Table 20-1, p.65).
  18. ↑ Jorgensen (1991, Table 22-1, p.72). Jorgensen's table 22-1 is given for an equal temperament tuned to a pitch 6.58097 cents lower than standard, so that the pitch of its A will coincide with that of his equal-beating Vallotti. The table given here is for an equal temperament at standard pitch. Its entries are those of Jorgensen's Table 22-1 decreased by 6.58097 cents and rounded to one decimal place.

Related Research Articles

<span class="mw-page-title-main">Just intonation</span> Musical tuning based on pure intervals

In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth.

<span class="mw-page-title-main">Pythagorean tuning</span> Method of tuning a musical instrument

Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2. This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2, which is ≈ 702 cents wide.

<span class="mw-page-title-main">Meantone temperament</span> Musical tuning system

Meantone temperaments are musical temperaments, that is a variety of tuning systems, obtained by narrowing the fifths so that their ratio is slightly less than 3:2, in order to push the thirds closer to pure. Meantone temperaments are constructed similarly to Pythagorean tuning, as a stack of equal fifths, but they are temperaments in that the fifths are not pure.

In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.

<span class="mw-page-title-main">Chromatic scale</span> Musical scale set of twelve pitches

The chromatic scale is a set of twelve pitches used in tonal music, with notes separated by the interval of a semitone. Chromatic instruments, such as the piano, are made to produce the chromatic scale, while other instruments capable of continuously variable pitch, such as the trombone and violin, can also produce microtones, or notes between those available on a piano.

<span class="mw-page-title-main">Wolf interval</span> Dissonant musical interval

In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament. More broadly, it is also used to refer to similar intervals produced by other tuning systems, including Pythagorean and most meantone temperaments.

In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B♯, or D♭ and C♯. It is equal to the frequency ratio (1.5)12⁄27 = 531441⁄524288 ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often "temper" is the Pythagorean comma.

<span class="mw-page-title-main">Diesis</span> An interval in classical music

In classical music from Western culture, a diesis is either an accidental, or a very small musical interval, usually defined as the difference between an octave and three justly tuned major thirds, equal to 128:125 or about 41.06 cents. In 12-tone equal temperament three major thirds in a row equal an octave, but three justly-tuned major thirds fall quite a bit narrow of an octave, and the diesis describes the amount by which they are short. For instance, an octave (2:1) spans from C to C', and three justly tuned major thirds (5:4) span from C to B♯. The difference between C-C' (2:1) and C-B♯ (125:64) is the diesis (128:125). Notice that this coincides with the interval between B♯ and C', also called a diminished second.

<span class="mw-page-title-main">Circle of fifths</span> Relationship among tones of the chromatic scale

In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths.. If C is chosen as a starting point, the sequence is: C, G, D, A, E, B, F♯, C♯, A♭, E♭, B♭, F. Continuing the pattern from F returns the sequence to its starting point of C. This order places the most closely related key signatures adjacent to one another. It is usually illustrated in the form of a circle.

A schismatic temperament is a musical tuning system that results from tempering the schisma of 32805:32768 to a unison. It is also called the schismic temperament, Helmholtz temperament, or quasi-Pythagorean temperament.

<span class="mw-page-title-main">Comma (music)</span> Very small interval arising from discrepancies in tuning

In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Strictly speaking, there are only two kinds of comma, the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.

Quarter-comma meantone, or 1⁄4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma (81 : 80), with respect to its just intonation used in Pythagorean tuning ; the result is 3/2 × 1⁄4 = 4√5 ≈ 1.49535, or a fifth of 696.578 cents. This fifth is then iterated to generate the diatonic scale and other notes of the temperament. The purpose is to obtain justly intoned major thirds. It was described by Pietro Aron in his Toscanello de la Musica of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible." Later theorists Gioseffo Zarlino and Francisco de Salinas described the tuning with mathematical exactitude.

<span class="mw-page-title-main">53 equal temperament</span> Musical tuning system with 53 pitches equally-spaced on a logarithmic scale

In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps. Each step represents a frequency ratio of 21⁄53, or 22.6415 cents, an interval sometimes called the Holdrian comma.

In music, septimal meantone temperament, also called standard septimal meantone or simply septimal meantone, refers to the tempering of 7-limit musical intervals by a meantone temperament tuning in the range from fifths flattened by the amount of fifths for 12 equal temperament to those as flat as 19 equal temperament, with 31 equal temperament being a more or less optimal tuning for both the 5- and 7-limits. Meantone temperament represents a frequency ratio of approximately 5 by means of four fifths, so that the major third, for instance C–E, is obtained from two tones in succession. Septimal meantone represents the frequency ratio of 56 (7 × 23) by ten fifths, so that the interval 7:4 is reached by five successive tones. Hence C–A♯, not C–B♭, represents a 7:4 interval in septimal meantone.

In music, 22 equal temperament, called 22-TET, 22-EDO, or 22-ET, is the tempered scale derived by dividing the octave into 22 equal steps. Each step represents a frequency ratio of 22√2, or 54.55 cents.

Kirnberger temperament is an irregular temperament developed in the second half of the 18th century by Johann Kirnberger. Kirnberger was a student of Johann Sebastian Bach, held great admiration for his teacher and was one of his principal proponents.

<span class="mw-page-title-main">Diminished second</span> Musical interval

In modern Western tonal music theory, a diminished second is the interval produced by narrowing a minor second by one chromatic semitone. In twelve-tone equal temperament, it is enharmonically equivalent to a perfect unison.; therefore, it is the interval between notes on two adjacent staff positions, or having adjacent note letters, altered in such a way that they have no pitch difference in twelve-tone equal temperament. An example is the interval from a B to the C♭ immediately above; another is the interval from a B♯ to the C immediately above.

Werckmeister temperaments are the tuning systems described by Andreas Werckmeister in his writings. The tuning systems are numbered in two different ways: the first refers to the order in which they were presented as "good temperaments" in Werckmeister's 1691 treatise, the second to their labelling on his monochord. The monochord labels start from III since just intonation is labelled I and quarter-comma meantone is labelled II. The temperament commonly known as "Werckmeister III" is referred to in this article as "Werckmeister I (III)".

"Young temperament" may refer to either of a pair of circulating temperaments described by Thomas Young in a letter dated July 9, 1799, to the Royal Society of London. The letter was read at the Society's meeting of January 16, 1800, and included in its Philosophical Transactions for that year. The temperaments are referred to individually as "Young's first temperament" and "Young's second temperament", more briefly as "Young's No. 1" and "Young's No. 2", or with some other variations of these expressions.

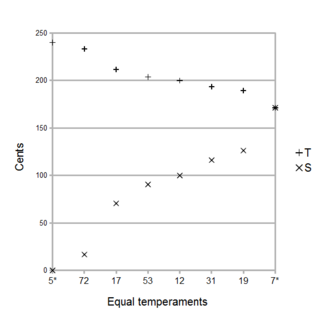
<span class="mw-page-title-main">Regular diatonic tuning</span>

A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's. In such a tuning, then the notes are connected together in a chain of seven fifths, all the same size which makes it a Linear temperament with the tempered fifth as a generator.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.