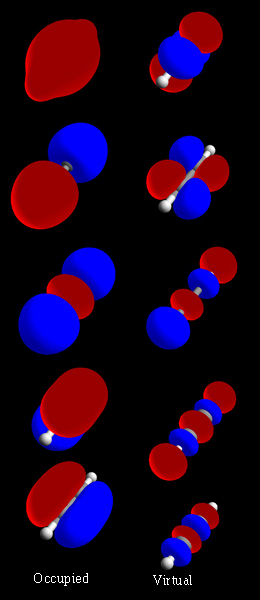
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms atomic orbital and molecular orbital were introduced by Robert S. Mulliken in 1932 to mean one-electron orbital wave functions. At an elementary level, they are used to describe the region of space in which a function has a significant amplitude.

In abstract algebra, group theory studies the algebraic structures known as groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right.
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions. In a mathematical sense, these wave functions are the basis set of functions, the basis functions, which describe the electrons of a given atom. In chemical reactions, orbital wavefunctions are modified, i.e. the electron cloud shape is changed, according to the type of atoms participating in the chemical bond.
Rotational–vibrational spectroscopy is a branch of molecular spectroscopy that is concerned with infrared and Raman spectra of molecules in the gas phase. Transitions involving changes in both vibrational and rotational states can be abbreviated as rovibrational transitions. When such transitions emit or absorb photons, the frequency is proportional to the difference in energy levels and can be detected by certain kinds of spectroscopy. Since changes in rotational energy levels are typically much smaller than changes in vibrational energy levels, changes in rotational state are said to give fine structure to the vibrational spectrum. For a given vibrational transition, the same theoretical treatment as for pure rotational spectroscopy gives the rotational quantum numbers, energy levels, and selection rules. In linear and spherical top molecules, rotational lines are found as simple progressions at both higher and lower frequencies relative to the pure vibration frequency. In symmetric top molecules the transitions are classified as parallel when the dipole moment change is parallel to the principal axis of rotation, and perpendicular when the change is perpendicular to that axis. The ro-vibrational spectrum of the asymmetric rotor water is important because of the presence of water vapor in the atmosphere.
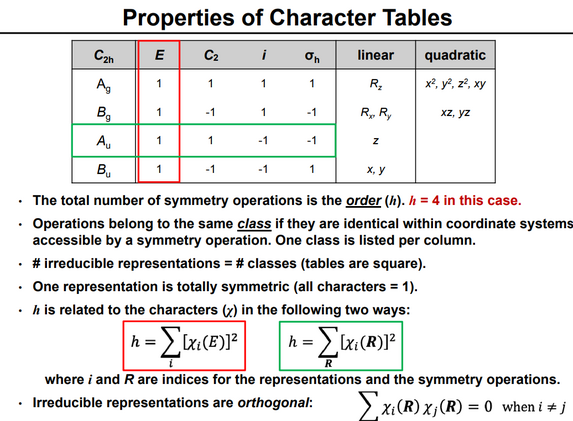
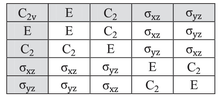
In group theory, a branch of abstract algebra, a character table is a two-dimensional table whose rows correspond to irreducible representations, and whose columns correspond to conjugacy classes of group elements. The entries consist of characters, the traces of the matrices representing group elements of the column's class in the given row's group representation. In chemistry, crystallography, and spectroscopy, character tables of point groups are used to classify e.g. molecular vibrations according to their symmetry, and to predict whether a transition between two states is forbidden for symmetry reasons. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry devote a chapter to the use of symmetry group character tables.
The Schoenfliesnotation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is often sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation.

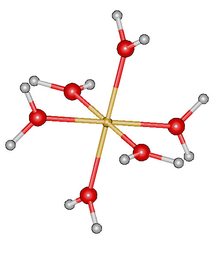
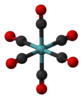
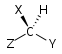
Molecular geometry is the three-dimensional arrangement of the atoms that constitute a molecule. It includes the general shape of the molecule as well as bond lengths, bond angles, torsional angles and any other geometrical parameters that determine the position of each atom.
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it can also refer to the simultaneous flip in the sign of all three spatial coordinates :
In physics and chemistry, a selection rule, or transition rule, formally constrains the possible transitions of a system from one quantum state to another. Selection rules have been derived for electromagnetic transitions in molecules, in atoms, in atomic nuclei, and so on. The selection rules may differ according to the technique used to observe the transition. The selection rule also plays a role in chemical reactions, where some are formally spin-forbidden reactions, that is, reactions where the spin state changes at least once from reactants to products.

In mathematics, D3 (sometimes alternatively denoted by D6) is the dihedral group of degree 3 and order 6. It equals the symmetric group S3. It is also the smallest non-abelian group.
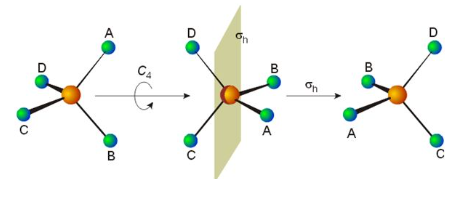
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.
A molecular orbital diagram, or MO diagram, is a qualitative descriptive tool explaining chemical bonding in molecules in terms of molecular orbital theory in general and the linear combination of atomic orbitals (LCAO) method in particular. A fundamental principle of these theories is that as atoms bond to form molecules, a certain number of atomic orbitals combine to form the same number of molecular orbitals, although the electrons involved may be redistributed among the orbitals. This tool is very well suited for simple diatomic molecules such as dihydrogen, dioxygen, and carbon monoxide but becomes more complex when discussing even comparatively simple polyatomic molecules, such as methane. MO diagrams can explain why some molecules exist and others do not. They can also predict bond strength, as well as the electronic transitions that can take place.
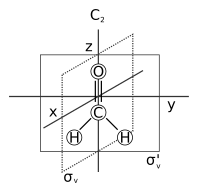
In chemistry and crystallography, a symmetry element is a point, line, or plane about which symmetry operations can take place. In particular, a symmetry element can be a mirror plane, an axis of rotation, or a center of inversion. For an object such as a molecule or a crystal, a symmetry element corresponds to a set of symmetry operations, which are the rigid transformations employing the symmetry element that leave the object unchanged. The set containing these operations form one of the symmetry groups of the object. The elements of this symmetry group should not be confused with the "symmetry element" itself. Loosely, a symmetry element is the geometric set of fixed points of a symmetry operation. For example, for rotation about an axis, the points on the axis do not move and in a reflection the points that remain unchanged make up a plane of symmetry.
A molecular vibration is a periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The typical vibrational frequencies range from less than 1013 Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 µm.
In mathematics, a symmetry operation is a geometric transformation of an object that leaves the object looking the same after it has been carried out. For example, a 1⁄3 turn rotation of a regular triangle about its center, a reflection of a square across its diagonal, a translation of the Euclidean plane, or a point reflection of a sphere through its center are all symmetry operations. Each symmetry operation is performed with respect to some symmetry element. Symmetry operations can be classified either as point symmetry operations or as travel symmetry operations.

In geometry, a point reflection is a transformation of affine space in which every point is reflected across a specific fixed point. When dealing with crystal structures and in the physical sciences the terms inversion symmetry, inversion center or centrosymmetric are more commonly used.
The rule of mutual exclusion in molecular spectroscopy relates the observation of molecular vibrations to molecular symmetry. It states that no normal modes can be both Infrared and Raman active in a molecule that possesses a center of symmetry. This is a powerful application of group theory to vibrational spectroscopy, and allows one to easily detect the presence of this symmetry element by comparison of the IR and Raman spectra generated by the same molecule.
Molecular symmetry in physics and chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in the application of Quantum Mechanics in physics and chemistry, for example it can be used to predict or explain many of a molecule's properties, such as its dipole moment and its allowed spectroscopic transitions, without doing the exact rigorous calculations. To do this it is necessary to classify the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Among all the molecular symmetries, diatomic molecules show some distinct features and they are relatively easier to analyze.
To determine the vibrational spectroscopy of linear molecules, the rotation and vibration of linear molecules are taken into account to predict which vibrational (normal) modes are active in the infrared spectrum and the Raman spectrum.



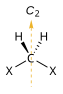




































![[Fe(Me5-Cp)(P5)] (Fe(Me5-Cp)(P5)).png](http://upload.wikimedia.org/wikipedia/commons/thumb/9/97/%28Fe%28Me5-Cp%29%28P5%29%29.png/220px-%28Fe%28Me5-Cp%29%28P5%29%29.png)



![(d,d)-trans-[Co(en)2Cl2] (d,d)-trans-(Co(en)2Cl2)+.png](http://upload.wikimedia.org/wikipedia/commons/thumb/5/5d/%28%CE%B4%2C%CE%B4%29-trans-%28Co%28en%292Cl2%29%2B.png/220px-%28%CE%B4%2C%CE%B4%29-trans-%28Co%28en%292Cl2%29%2B.png)

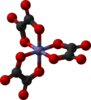


















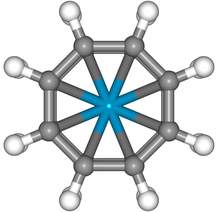




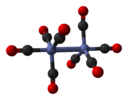
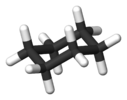


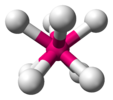








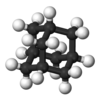
![[Fe(C5H5N)6] (Fe(C5H5N)6)2+.png](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1a/%28Fe%28C5H5N%296%292%2B.png/220px-%28Fe%28C5H5N%296%292%2B.png)
![[Th(NO3)6] (Th(NO3)6)2-.png](http://upload.wikimedia.org/wikipedia/commons/thumb/c/ce/%28Th%28NO3%296%292-.png/220px-%28Th%28NO3%296%292-.png)