Control theory is a field of control engineering and applied mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any delay, overshoot, or steady-state error and ensuring a level of control stability; often with the aim to achieve a degree of optimality.
An electronic oscillator is an electronic circuit that produces a periodic, oscillating or alternating current (AC) signal, usually a sine wave, square wave or a triangle wave, powered by a direct current (DC) source. Oscillators are found in many electronic devices, such as radio receivers, television sets, radio and television broadcast transmitters, computers, computer peripherals, cellphones, radar, and many other devices.

In mathematics, the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories. Quantitatively, two trajectories in phase space with initial separation vector diverge at a rate given by

Negative feedback occurs when some function of the output of a system, process, or mechanism is fed back in a manner that tends to reduce the fluctuations in the output, whether caused by changes in the input or by other disturbances. A classic example of negative feedback is a heating system thermostat — when the temperature gets high enough, the heater is turned OFF. When the temperature gets too cold, the heat is turned back ON. In each case the "feedback" generated by the thermostat "negates" the trend.
Various types of stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Aleksandr Lyapunov. In simple terms, if the solutions that start out near an equilibrium point stay near forever, then is Lyapunov stable. More strongly, if is Lyapunov stable and all solutions that start out near converge to , then is said to be asymptotically stable. The notion of exponential stability guarantees a minimal rate of decay, i.e., an estimate of how quickly the solutions converge. The idea of Lyapunov stability can be extended to infinite-dimensional manifolds, where it is known as structural stability, which concerns the behavior of different but "nearby" solutions to differential equations. Input-to-state stability (ISS) applies Lyapunov notions to systems with inputs.
Observability is a measure of how well internal states of a system can be inferred from knowledge of its external outputs.
Vasile Mihai Popov is a leading systems theorist and control engineering specialist. He is well known for having developed a method to analyze stability of nonlinear dynamical systems, now known as Popov criterion.
In control systems theory, the describing function (DF) method, developed by Nikolay Mitrofanovich Krylov and Nikolay Bogoliubov in the 1930s, and extended by Ralph Kochenburger is an approximate procedure for analyzing certain nonlinear control problems. It is based on quasi-linearization, which is the approximation of the non-linear system under investigation by a linear time-invariant (LTI) transfer function that depends on the amplitude of the input waveform. By definition, a transfer function of a true LTI system cannot depend on the amplitude of the input function because an LTI system is linear. Thus, this dependence on amplitude generates a family of linear systems that are combined in an attempt to capture salient features of the non-linear system behavior. The describing function is one of the few widely applicable methods for designing nonlinear systems, and is very widely used as a standard mathematical tool for analyzing limit cycles in closed-loop controllers, such as industrial process controls, servomechanisms, and electronic oscillators.
The Kalman–Yakubovich–Popov lemma is a result in system analysis and control theory which states: Given a number , two n-vectors B, C and an n x n Hurwitz matrix A, if the pair is completely controllable, then a symmetric matrix P and a vector Q satisfying
In mathematics, the Markus–Yamabe conjecture is a conjecture on global asymptotic stability. If the Jacobian matrix of a dynamical system at a fixed point is Hurwitz, then the fixed point is asymptotically stable. Markus-Yamabe conjecture asks if a similar result holds globally. Precisely, the conjecture states that if a continuously differentiable map on an -dimensional real vector space has a fixed point, and its Jacobian matrix is everywhere Hurwitz, then the fixed point is globally stable.
In control theory, a separation principle, more formally known as a principle of separation of estimation and control, states that under some assumptions the problem of designing an optimal feedback controller for a stochastic system can be solved by designing an optimal observer for the state of the system, which feeds into an optimal deterministic controller for the system. Thus the problem can be broken into two separate parts, which facilitates the design.
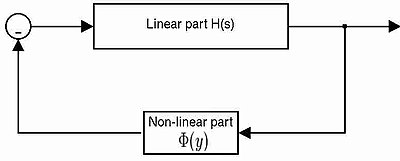
In nonlinear control, Aizerman's conjecture or Aizerman problem states that a linear system in feedback with a sector nonlinearity would be stable if the linear system is stable for any linear gain of the sector. This conjecture, proposed by Mark Aronovich Aizerman in 1949, was proven false but led to the (valid) sufficient criteria on absolute stability.
In nonlinear control and stability theory, the circle criterion is a stability criterion for nonlinear time-varying systems. It can be viewed as a generalization of the Nyquist stability criterion for linear time-invariant (LTI) systems.
In mathematical physics and the theory of partial differential equations, the solitary wave solution of the form is said to be orbitally stable if any solution with the initial data sufficiently close to forever remains in a given small neighborhood of the trajectory of
In the bifurcation theory, a bounded oscillation that is born without loss of stability of stationary set is called a hidden oscillation. In nonlinear control theory, the birth of a hidden oscillation in a time-invariant control system with bounded states means crossing a boundary, in the domain of the parameters, where local stability of the stationary states implies global stability. If a hidden oscillation attracts all nearby oscillations, then it is called a hidden attractor. For a dynamical system with a unique equilibrium point that is globally attractive, the birth of a hidden attractor corresponds to a qualitative change in behaviour from monostability to bi-stability. In the general case, a dynamical system may turn out to be multistable and have coexisting local attractors in the phase space. While trivial attractors, i.e. stable equilibrium points, can be easily found analytically or numerically, the search of periodic and chaotic attractors can turn out to be a challenging problem.
Kalman's conjecture or Kalman problem is a disproved conjecture on absolute stability of nonlinear control system with one scalar nonlinearity, which belongs to the sector of linear stability. Kalman's conjecture is a strengthening of Aizerman's conjecture and is a special case of Markus–Yamabe conjecture. This conjecture was proven false but led to the (valid) sufficient criteria on absolute stability.
Moving horizon estimation (MHE) is an optimization approach that uses a series of measurements observed over time, containing noise and other inaccuracies, and produces estimates of unknown variables or parameters. Unlike deterministic approaches, MHE requires an iterative approach that relies on linear programming or nonlinear programming solvers to find a solution.
In nonlinear control and stability theory, the Popov criterion is a stability criterion discovered by Vasile M. Popov for the absolute stability of a class of nonlinear systems whose nonlinearity must satisfy an open-sector condition. While the circle criterion can be applied to nonlinear time-varying systems, the Popov criterion is applicable only to autonomous systems.
Nikolay Vladimirovich Kuznetsov is a specialist in nonlinear dynamics and control theory.
William F. Egan was well-known expert and author in the area of PLLs. The first and second editions of his book Frequency Synthesis by Phase Lock as well as his book Phase-Lock Basics are references among electrical engineers specializing in areas involving PLLs.