The Mach number, often only Mach, is a dimensionless quantity in fluid dynamics representing the ratio of flow velocity past a boundary to the local speed of sound. It is named after the Austrian physicist and philosopher Ernst Mach.

In fluid dynamics, potential flow is the ideal flow pattern of an inviscid fluid. Potential flows are described and determined by mathematical methods.

In thermodynamics and fluid mechanics, the compressibility is a measure of the instantaneous relative volume change of a fluid or solid as a response to a pressure change. In its simple form, the compressibility may be expressed as
Compressible flow is the branch of fluid mechanics that deals with flows having significant changes in fluid density. While all flows are compressible, flows are usually treated as being incompressible when the Mach number is smaller than 0.3. The study of compressible flow is relevant to high-speed aircraft, jet engines, rocket motors, high-speed entry into a planetary atmosphere, gas pipelines, commercial applications such as abrasive blasting, and many other fields.

The Rankine–Hugoniot conditions, also referred to as Rankine–Hugoniot jump conditions or Rankine–Hugoniot relations, describe the relationship between the states on both sides of a shock wave or a combustion wave in a one-dimensional flow in fluids or a one-dimensional deformation in solids. They are named in recognition of the work carried out by Scottish engineer and physicist William John Macquorn Rankine and French engineer Pierre Henri Hugoniot.
The Knudsen number (Kn) is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale. This length scale could be, for example, the radius of a body in a fluid. The number is named after Danish physicist Martin Knudsen (1871–1949).
Rayleigh flow refers to frictionless, non-adiabatic flow through a constant area duct where the effect of heat addition or rejection is considered. Compressibility effects often come into consideration, although the Rayleigh flow model certainly also applies to incompressible flow. For this model, the duct area remains constant and no mass is added within the duct. Therefore, unlike Fanno flow, the stagnation temperature is a variable. The heat addition causes a decrease in stagnation pressure, which is known as the Rayleigh effect and is critical in the design of combustion systems. Heat addition will cause both supersonic and subsonic Mach numbers to approach Mach 1, resulting in choked flow. Conversely, heat rejection decreases a subsonic Mach number and increases a supersonic Mach number along the duct. It can be shown that for calorically perfect flows the maximum entropy occurs at M = 1. Rayleigh flow is named after John Strutt, 3rd Baron Rayleigh.
Choked flow is a compressible flow effect. The parameter that becomes "choked" or "limited" is the fluid velocity.

The Chapman–Jouguet condition holds approximately in detonation waves in high explosives. It states that the detonation propagates at a velocity at which the reacting gases just reach sonic velocity as the reaction ceases.
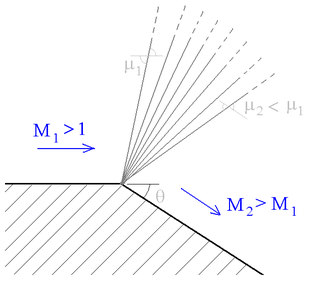
A supersonic expansion fan, technically known as Prandtl–Meyer expansion fan, a two-dimensional simple wave, is a centered expansion process that occurs when a supersonic flow turns around a convex corner. The fan consists of an infinite number of Mach waves, diverging from a sharp corner. When a flow turns around a smooth and circular corner, these waves can be extended backwards to meet at a point.
In fluid dynamics, a moving shock is a shock wave that is travelling through a fluid medium with a velocity relative to the velocity of the fluid already making up the medium. As such, the normal shock relations require modification to calculate the properties before and after the moving shock. A knowledge of moving shocks is important for studying the phenomena surrounding detonation, among other applications.
Fanno flow is the adiabatic flow through a constant area duct where the effect of friction is considered. Compressibility effects often come into consideration, although the Fanno flow model certainly also applies to incompressible flow. For this model, the duct area remains constant, the flow is assumed to be steady and one-dimensional, and no mass is added within the duct. The Fanno flow model is considered an irreversible process due to viscous effects. The viscous friction causes the flow properties to change along the duct. The frictional effect is modeled as a shear stress at the wall acting on the fluid with uniform properties over any cross section of the duct.
Shock is an abrupt discontinuity in the flow field and it occurs in flows when the local flow speed exceeds the local sound speed. More specifically, it is a flow whose Mach number exceeds 1.
In aerodynamics, the normal shock tables are a series of tabulated data listing the various properties before and after the occurrence of a normal shock wave. With a given upstream Mach number, the post-shock Mach number can be calculated along with the pressure, density, temperature, and stagnation pressure ratios. Such tables are useful since the equations used to calculate the properties after a normal shock are cumbersome.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to
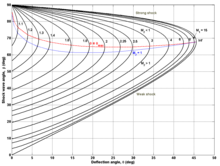
The term shock polar is generally used with the graphical representation of the Rankine–Hugoniot equations in either the hodograph plane or the pressure ratio-flow deflection angle plane. The polar itself is the locus of all possible states after an oblique shock.

Isentropic expansion waves are created when a supersonic flow is redirected along a curved surface. These waves are studied to obtain a relation between deflection angle and Mach number. Each wave in this case is a Mach wave, so it is at an angle , where M is the Mach number immediately before the wave. Expansion waves are divergent because as the flow expands the value of Mach number increases, thereby decreasing the Mach angle.
Isentropic nozzle flow describes the movement of a gas or fluid through a narrowing opening without an increase or decrease in entropy.
In the field of mathematics known as complex analysis, the indicator function of an entire function indicates the rate of growth of the function in different directions.