Opening (morphology)

Last updated June 07, 2024

The opening of the dark-blue square by a disk, resulting in the light-blue square with round corners. Opening.png — The opening of the dark-blue square by a disk, resulting in the light-blue square with round corners.

In mathematical morphology, opening is the dilation of the erosion of a set A by a structuring element B:

Together with closing, the opening serves in computer vision and image processing as a basic workhorse of morphological noise removal. Opening removes small objects from the foreground (usually taken as the bright pixels) of an image, placing them in the background, while closing removes small holes in the foreground, changing small islands of background into foreground. These techniques can also be used to find specific shapes in an image. Opening can be used to find things into which a specific structuring element can fit (edges, corners, ...).

One can think of B sweeping around the inside of the boundary of A, so that it does not extend beyond the boundary, and shaping the A boundary around the boundary of the element.

Properties

Opening is idempotent, that is, $(A\circ B)\circ B=A\circ B$ .
Opening is increasing, that is, if $A\subseteq C$ , then $A\circ B\subseteq C\circ B$ .
Opening is anti-extensive, i.e., $A\circ B\subseteq A$ .
Opening is translation invariant.
Opening and closing satisfy the duality $A\bullet B=(A^{c}\circ B^{c})^{c}$ , where $\bullet$ denotes closing.

Example

Perform Erosion $(A\ominus B)$ :

Suppose A is the following 16 x 15 matrix and B is the following 3 x 3 matrix:

   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0    0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0    0 0 1 1 1 1 1 0 0 0 0 1 1 1 0 0     0 0 1 1 1 1 1 0 0 0 1 1 1 1 0 0     1 1 1    0 0 1 1 1 1 0 0 0 1 1 1 1 1 0 0     1 1 1    0 0 0 1 1 0 0 0 1 1 1 1 1 0 0 0     1 1 1    0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0    0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0        0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0    0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0    0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0           0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0    0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

First, perform Erosion on A by B $(A\ominus B$ ):

Assuming that the origin of B is at its center, for each pixel in A superimpose the origin of B, if B is completely contained by A the pixel is retained, else deleted.

Therefore the Erosion of A by B is given by this 16 x 15 matrix.

$(A\ominus B)$ is given by:

   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0    0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0    0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0    0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0    0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0    0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0    0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0    0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0    0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0    0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0    0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Then, perform Dilation on the result of Erosion by B: $(A\ominus B)\oplus B$ :

For each pixel in $(A\ominus B)$ that has a value of 1, superimpose B, with the center of B aligned with the corresponding pixel in $(A\ominus B)$ .

Each pixel of every superimposed B is included in the dilation of A by B.

The dilation of $(A\ominus B)$ by B is given by this 16 x 15 matrix.

$(A\ominus B)\oplus B$ is given by :

   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0    0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0    0 0 1 1 1 1 0 0 0 0 0 1 1 1 0 0     0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0       0 0 1 1 1 1 0 0 0 1 1 1 1 1 0 0         0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0         0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0    0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0        0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0    0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0    0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0           0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0    0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Therefore, the opening operation $A\circ B$ removes small protrusions from the boundary of the object represented by A, while preserving the overall shape and size of the larger components.

Extension: Opening by reconstruction

In morphological opening $(A\ominus B)\oplus B$ , the erosion operation removes objects that are smaller than structuring element B and the dilation operation (approximately) restores the size and shape of the remaining objects. However, restoration accuracy in the dilation operation depends highly on the type of structuring element and the shape of the restoring objects. The opening by reconstruction method is able to restore the objects more completely after erosion has been applied. It is defined as the reconstruction by geodesic dilation of $n$ erosions of $F$ by $B$ with respect to $F$ :

$O_{R}^{(n)}(F)=R_{F}^{D}[(F\ominus nB)],$ ^[1]

where $(F\ominus nB)$ denotes a marker image and $F$ is a mask image in morphological reconstruction by dilation. $R_{F}^{D}[(F\ominus nB)]=D_{F}^{(k)}[(F\ominus nB)],$ ^[1] $D$ denotes geodesic dilation with $k$ iterations until stability, i.e., such that $D_{F}^{(k)}[(F\ominus nB)]=D_{F}^{(k-1)}[(F\ominus nB)].$ ^[1] Since $D_{F}^{(1)}[(F\ominus nB)]=([(F\ominus nB)]\oplus B)\cap F$ ,^[1] the marker image is limited in the growth region by the mask image, so the dilation operation on the marker image will not expand beyond the mask image. As a result, the marker image is a subset of the mask image $(F\ominus nB)\subseteq F.$ ^[1] (Strictly, this holds for binary masks only. However, similar statements hold when the mask is not binary.)

The images below present a simple opening-by-reconstruction example which extracts the vertical strokes from an input text image. Since the original image is converted from grayscale to binary image, it has a few distortions in some characters so that same characters might have different vertical lengths. In this case, the structuring element is an 8-pixel vertical line which is applied in the erosion operation in order to find objects of interest. Moreover, morphological reconstruction by dilation, $R_{F}^{D}[(F\ominus nB)]=D_{F}^{(k)}[(F\ominus nB)]$ ^[1] iterates $k=9$ times until the resulting image converges.

Marker image

Result of opening by reconstruction

Bibliography

Image Analysis and Mathematical Morphology by Jean Serra, ISBN 0-12-637240-3 (1982)
Image Analysis and Mathematical Morphology, Volume 2: Theoretical Advances by Jean Serra, ISBN 0-12-637241-1 (1988)
An Introduction to Morphological Image Processing by Edward R. Dougherty, ISBN 0-8194-0845-X (1992)

External links

http://homepages.inf.ed.ac.uk/rbf/HIPR2/open.htm - Morphological Opening

Related Research Articles

In mathematics, specifically abstract algebra, the isomorphism theorems are theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures. In universal algebra, the isomorphism theorems can be generalized to the context of algebras and congruences.

In category theory and its applications to mathematics, a biproduct of a finite collection of objects, in a category with zero objects, is both a product and a coproduct. In a preadditive category the notions of product and coproduct coincide for finite collections of objects. The biproduct is a generalization of finite direct sums of modules.

In mathematics, specifically in category theory, an additive category is a preadditive category C admitting all finitary biproducts.

A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula. As formulas are entirely constituted with symbols of various types, many symbols are needed for expressing all mathematics.

Digital image processing is the use of a digital computer to process digital images through an algorithm. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing. It allows a much wider range of algorithms to be applied to the input data and can avoid problems such as the build-up of noise and distortion during processing. Since images are defined over two dimensions digital image processing may be modeled in the form of multidimensional systems. The generation and development of digital image processing are mainly affected by three factors: first, the development of computers; second, the development of mathematics ; third, the demand for a wide range of applications in environment, agriculture, military, industry and medical science has increased.

An exact sequence is a sequence of morphisms between objects such that the image of one morphism equals the kernel of the next.

<span class="mw-page-title-main">Mathematical morphology</span>

Mathematical morphology (MM) is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions. MM is most commonly applied to digital images, but it can be employed as well on graphs, surface meshes, solids, and many other spatial structures.

<span class="mw-page-title-main">Erosion (morphology)</span> Basic operation in mathematical morphology

Erosion is one of two fundamental operations in morphological image processing from which all other morphological operations are based. It was originally defined for binary images, later being extended to grayscale images, and subsequently to complete lattices. The erosion operation usually uses a structuring element for probing and reducing the shapes contained in the input image.

Dilation is one of the basic operations in mathematical morphology. Originally developed for binary images, it has been expanded first to grayscale images, and then to complete lattices. The dilation operation usually uses a structuring element for probing and expanding the shapes contained in the input image.

<span class="mw-page-title-main">Closing (morphology)</span>

In mathematical morphology, the closing of a set A by a structuring element B is the erosion of the dilation of that set,

In mathematical morphology, a structuring element is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image. It is typically used in morphological operations, such as dilation, erosion, opening, and closing, as well as the hit-or-miss transform.

The direct sum is an operation between structures in abstract algebra, a branch of mathematics. It is defined differently, but analogously, for different kinds of structures. As an example, the direct sum of two abelian groups $and is another abelian group consisting of the ordered pairs where and . To add ordered pairs, we define the sum to be; in other words addition is defined coordinate-wise. For example, the direct sum, where is real coordinate space, is the Cartesian plane, . A similar process can be used to form the direct sum of two vector spaces or two modules.$

In the mathematics of binary relations, the composition of relations is the forming of a new binary relation R; S from two given binary relations R and S. In the calculus of relations, the composition of relations is called relative multiplication, and its result is called a relative product. Function composition is the special case of composition of relations where all relations involved are functions.

In mathematical morphology, hit-or-miss transform is an operation that detects a given configuration in a binary image, using the morphological erosion operator and a pair of disjoint structuring elements. The result of the hit-or-miss transform is the set of positions where the first structuring element fits in the foreground of the input image, and the second structuring element misses it completely.

In digital image processing, morphological skeleton is a skeleton representation of a shape or binary image, computed by means of morphological operators.

In mathematical morphology and digital image processing, a morphological gradient is the difference between the dilation and the erosion of a given image. It is an image where each pixel value indicates the contrast intensity in the close neighborhood of that pixel. It is useful for edge detection and segmentation applications.

In mathematical morphology and digital image processing, a top-hat transform is an operation that extracts small elements and details from given images. There exist two types of top-hat transform: the white top-hat transform is defined as the difference between the input image and its opening by some structuring element, while the black top-hat transform is defined dually as the difference between the closing and the input image. Top-hat transforms are used for various image processing tasks, such as feature extraction, background equalization, image enhancement, and others.

In mathematical morphology, granulometry is an approach to compute a size distribution of grains in binary images, using a series of morphological opening operations. It was introduced by Georges Matheron in the 1960s, and is the basis for the characterization of the concept of size in mathematical morphology.

Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on $. Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The classical theorem of Stokes can be stated in one sentence: The line integral of a vector field over a loop is equal to the surface integral of its curl over the enclosed surface. It is illustrated in the figure, where the direction of positive circulation of the bounding contour \partialΣ, and the direction n of positive flux through the surface Σ, are related by a right-hand-rule. For the right hand the fingers circulate along \partialΣ and the thumb is directed along n .$

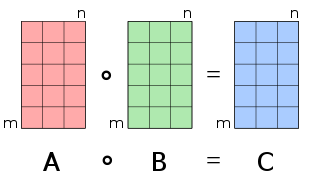
In mathematics, the Hadamard product is a binary operation that takes in two matrices of the same dimensions and returns a matrix of the multiplied corresponding elements. This operation can be thought as a "naive matrix multiplication" and is different from the matrix product. It is attributed to, and named after, either French mathematician Jacques Hadamard or German mathematician Issai Schur.

References

1 2 3 4 5 6 Woods}first=Richard E. (2016). Digital image processing. Pearson India Education Services. ISBN 9789332570320. OCLC 979415531.

Digital Image Processing (Third Edition) by Rafael C. Gonzalez and Richard E. Woods, ISBN 978-93-325-7032-0(2008)

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:0-1] 1 2 3 4 5 6 Woods}first=Richard E. (2016). Digital image processing. Pearson India Education Services. ISBN 9789332570320. OCLC 979415531.

[1]