
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all limiting values of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval [0,1] would be compact. Similarly, the space of rational numbers is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers is not compact either, because it excludes the two limiting values and . However, the extended real number linewould be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces.
In mathematics, a topological space is called separable if it contains a countable, dense subset; that is, there exists a sequence of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology.
In mathematics, a well-order on a set S is a total ordering on S with the property that every non-empty subset of S has a least element in this ordering. The set S together with the ordering is then called a well-ordered set. In some academic articles and textbooks these terms are instead written as wellorder, wellordered, and wellordering or well order, well ordered, and well ordering.
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement. Borel sets are named after Émile Borel.
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points. In a complete metric space, a closed set is a set which is closed under the limit operation. This should not be confused with a closed manifold.
In the mathematical field of topology, the Alexandroff extension is a way to extend a noncompact topological space by adjoining a single point in such a way that the resulting space is compact. It is named after the Russian mathematician Pavel Alexandroff. More precisely, let X be a topological space. Then the Alexandroff extension of X is a certain compact space X* together with an open embedding c : X → X* such that the complement of X in X* consists of a single point, typically denoted ∞. The map c is a Hausdorff compactification if and only if X is a locally compact, noncompact Hausdorff space. For such spaces the Alexandroff extension is called the one-point compactification or Alexandroff compactification. The advantages of the Alexandroff compactification lie in its simple, often geometrically meaningful structure and the fact that it is in a precise sense minimal among all compactifications; the disadvantage lies in the fact that it only gives a Hausdorff compactification on the class of locally compact, noncompact Hausdorff spaces, unlike the Stone–Čech compactification which exists for any topological space.

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology.
In topology, the long line is a topological space somewhat similar to the real line, but in a certain way "longer". It behaves locally just like the real line, but has different large-scale properties. Therefore, it serves as an important counterexample in topology. Intuitively, the usual real-number line consists of a countable number of line segments laid end-to-end, whereas the long line is constructed from an uncountable number of such segments.
In topology, a topological space is called a compactly generated space or k-space if its topology is determined by compact spaces in a manner made precise below. There is in fact no commonly agreed upon definition for such spaces, as different authors use variations of the definition that are not exactly equivalent to each other. Also some authors include some separation axiom in the definition of one or both terms, and others don't.
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space is said to be first-countable if each point has a countable neighbourhood basis. That is, for each point in there exists a sequence of neighbourhoods of such that for any neighbourhood of there exists an integer with contained in Since every neighborhood of any point contains an open neighborhood of that point, the neighbourhood basis can be chosen without loss of generality to consist of open neighborhoods.

Counterexamples in Topology is a book on mathematics by topologists Lynn Steen and J. Arthur Seebach, Jr.
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called "reals". It is denoted by NN, or ωω, or by the symbol or sometimes by ωω.
In mathematics, set-theoretic topology is a subject that combines set theory and general topology. It focuses on topological questions that are independent of Zermelo–Fraenkel set theory (ZFC).
In topology and related fields of mathematics, a sequential space is a topological space whose topology can be completely characterized by its convergent/divergent sequences. They can be thought of as spaces that satisfy a very weak axiom of countability, and all first-countable spaces are sequential.
In topology and related areas of mathematics, a subset A of a topological space X is said to be dense in X if every point of X either belongs to A or else is arbitrarily "close" to a member of A — for instance, the rational numbers are a dense subset of the real numbers because every real number either is a rational number or has a rational number arbitrarily close to it. Formally, is dense in if the smallest closed subset of containing is itself.
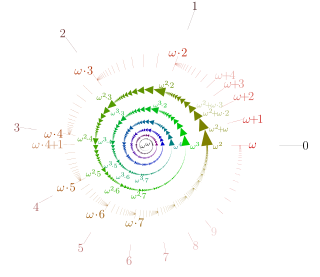
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.
This is a glossary of set theory.
In mathematics, a polyadic space is a topological space that is the image under a continuous function of a topological power of an Alexandroff one-point compactification of a discrete space.
















