
In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the distance between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate; the distance parameter could be any meaningful mono-dimensional measure of the process, such as time between production errors, or length along a roll of fabric in the weaving manufacturing process. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.

A logistic function or logistic curve is a common S-shaped curve with the equation
The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments, using various underlying assumptions. From the parabolic partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a unique price given the risk of the security and its expected return. The equation and model are named after economists Fischer Black and Myron Scholes; Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited.

Exponential growth is a process that increases quantity over time at an ever-increasing rate. It occurs when the instantaneous rate of change of a quantity with respect to time is proportional to the quantity itself. Described as a function, a quantity undergoing exponential growth is an exponential function of time, that is, the variable representing time is the exponent. Exponential growth is the inverse of logarithmic growth.

In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It models a broad range of random variables, largely in the nature of a time to failure or time between events. Examples are maximum one-day rainfalls and the time a user spends on a web page.

A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where N is the quantity and λ (lambda) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant:
The Lotka–Volterra equations, also known as the Lotka–Volterra predator–prey model, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:

Haldane's dilemma, also known as the waiting time problem, is a limit on the speed of beneficial evolution, calculated by J. B. S. Haldane in 1957. Before the invention of DNA sequencing technologies, it was not known how much polymorphism DNA harbored, although alloenzymes were beginning to make it clear that substantial polymorphism existed. This was puzzling because the amount of polymorphism known to exist seemed to exceed the theoretical limits that Haldane calculated, that is, the limits imposed if polymorphisms present in the population generally influence an organism's fitness. Motoo Kimura's landmark paper on neutral theory in 1968 built on Haldane's work to suggest that most molecular evolution is neutral, resolving the dilemma. Although neutral evolution remains the consensus theory among modern biologists, and thus Kimura's resolution of Haldane's dilemma is widely regarded as correct, some biologists argue that adaptive evolution explains a large fraction of substitutions in protein coding sequence, and they propose alternative solutions to Haldane's dilemma.
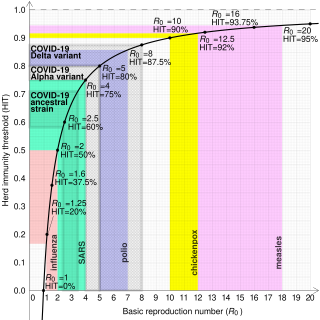
In epidemiology, the basic reproduction number, or basic reproductive number, denoted , of an infection is the expected number of cases directly generated by one case in a population where all individuals are susceptible to infection. The definition assumes that no other individuals are infected or immunized. Some definitions, such as that of the Australian Department of Health, add the absence of "any deliberate intervention in disease transmission". The basic reproduction number is not necessarily the same as the effective reproduction number , which is the number of cases generated in the current state of a population, which does not have to be the uninfected state. is a dimensionless number and not a time rate, which would have units of time−1, or units of time like doubling time.
Compartmental models are a very general modelling technique. They are often applied to the mathematical modelling of infectious diseases. The population is assigned to compartments with labels – for example, S, I, or R,. People may progress between compartments. The order of the labels usually shows the flow patterns between the compartments; for example SEIS means susceptible, exposed, infectious, then susceptible again.
Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes:
- To provide an analytical approximation to the posterior probability of the unobserved variables, in order to do statistical inference over these variables.
- To derive a lower bound for the marginal likelihood of the observed data. This is typically used for performing model selection, the general idea being that a higher marginal likelihood for a given model indicates a better fit of the data by that model and hence a greater probability that the model in question was the one that generated the data.
The birth–death process is a special case of continuous-time Markov process where the state transitions are of only two types: "births", which increase the state variable by one and "deaths", which decrease the state by one. It was introduced by William Feller. The model's name comes from a common application, the use of such models to represent the current size of a population where the transitions are literal births and deaths. Birth–death processes have many applications in demography, queueing theory, performance engineering, epidemiology, biology and other areas. They may be used, for example, to study the evolution of bacteria, the number of people with a disease within a population, or the number of customers in line at the supermarket.
The Gompertz curve or Gompertz function is a type of mathematical model for a time series, named after Benjamin Gompertz (1779–1865). It is a sigmoid function which describes growth as being slowest at the start and end of a given time period. The right-side or future value asymptote of the function is approached much more gradually by the curve than the left-side or lower valued asymptote. This is in contrast to the simple logistic function in which both asymptotes are approached by the curve symmetrically. It is a special case of the generalised logistic function. The function was originally designed to describe human mortality, but since has been modified to be applied in biology, with regard to detailing populations.
In population biology and demography, generation time is the average time between two consecutive generations in the lineages of a population. In human populations, generation time typically has ranged from 20 to 30 years, with wide variation based on gender and society. Historians sometimes use this to date events, by converting generations into years to obtain rough estimates of time.
In statistics, a power transform is a family of functions applied to create a monotonic transformation of data using power functions. It is a data transformation technique used to stabilize variance, make the data more normal distribution-like, improve the validity of measures of association, and for other data stabilization procedures.
A local volatility model, in mathematical finance and financial engineering, is an option pricing model that treats volatility as a function of both the current asset level and of time . As such, it is a generalisation of the Black–Scholes model, where the volatility is a constant. Local volatility models are often compared with stochastic volatility models, where the instantaneous volatility is not just a function of the asset level but depends also on a new "global" randomness coming from an additional random component.

In probability theory and statistics, the Conway–Maxwell–Poisson distribution is a discrete probability distribution named after Richard W. Conway, William L. Maxwell, and Siméon Denis Poisson that generalizes the Poisson distribution by adding a parameter to model overdispersion and underdispersion. It is a member of the exponential family, has the Poisson distribution and geometric distribution as special cases and the Bernoulli distribution as a limiting case.
In the study of age-structured population growth, probably one of the most important equations is the Euler–Lotka equation. Based on the age demographic of females in the population and female births, this equation allows for an estimation of how a population is growing.
Kermack–McKendrick theory is a hypothesis that predicts the number and distribution of cases of an infectious disease as it is transmitted through a population over time. Building on the research of Ronald Ross and Hilda Hudson, A. G. McKendrick and W. O. Kermack published their theory in a set of three articles from 1927, 1932, and 1933. While Kermack–McKendrick theory was indeed the source of SIR models and their relatives, Kermack and McKendrick were thinking of a more subtle and empirically useful problem than the simple compartmental models discussed here. The text is somewhat difficult to read, compared to modern papers, but the important feature is it was a model where the age-of-infection affected the transmission and removal rates.

The population dynamics of pest insects is a subject of interest to farmers, agricultural economists, ecologists, and those concerned with animal welfare.









![G. stearothermophilus has a shorter doubling time (td) than E. coli and N. meningitidis. Growth rates of 2 bacterial species will differ by unexpected orders of magnitude if the doubling times of the 2 species differ by even as little as 10 minutes. In eukaryotes such as animals, fungi, plants, and protists, doubling times are much longer than in bacteria. This reduces the growth rates of eukaryotes in comparison to Bacteria. G. stearothermophilus, E. coli, and N. meningitidis have 20 minute, 30 minute, and 40 minute doubling times under optimal conditions respectively. If bacterial populations could grow indefinitely (which they do not) then the number of bacteria in each species would approach infinity ([?]). However, the percentage of G. stearothermophilus bacteria out of all the bacteria would approach 100% whilst the percentage of E. coli and N. meningitidis combined out of all the bacteria would approach 0%. This graph is a simulation of this hypothetical scenario. In reality, bacterial populations do not grow indefinitely in size and the 3 species require different optimal conditions to bring their doubling times to minima.
Time in minutes
% that is G. stearothermophilus
30
44.4%
60
53.3%
90
64.9%
120
72.7%
-[?]
100%
Time in minutes
% that is E. coli
30
29.6%
60
26.7%
90
21.6%
120
18.2%
-[?]
0.00%
Time in minutes
% that is N. meningitidis
30
25.9%
60
20.0%
90
13.5%
120
9.10%
-[?]
0.00%
Disclaimer: Bacterial populations are logistic instead of geometric. Nevertheless, doubling times are applicable to both types of populations. G. stearothermophilus has a shorter doubling time (td) than E. coli and N. meningitidis.png](http://upload.wikimedia.org/wikipedia/commons/thumb/a/ae/G._stearothermophilus_has_a_shorter_doubling_time_%28td%29_than_E._coli_and_N._meningitidis.png/400px-G._stearothermophilus_has_a_shorter_doubling_time_%28td%29_than_E._coli_and_N._meningitidis.png)























