The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. This mathematical formalism uses mainly a part of functional analysis, especially Hilbert spaces, which are a kind of linear space. Such are distinguished from mathematical formalisms for physics theories developed prior to the early 1900s by the use of abstract mathematical structures, such as infinite-dimensional Hilbert spaces, and operators on these spaces. In brief, values of physical observables such as energy and momentum were no longer considered as values of functions on phase space, but as eigenvalues; more precisely as spectral values of linear operators in Hilbert space.

Quantum mechanics is a fundamental theory in physics that describes the behavior of nature at and below the scale of atoms. It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science.

The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position and momentum, can be simultaneously known. In other words, the more accurately one property is measured, the less accurately the other property can be known.

The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.

In quantum physics, a wave function is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters ψ and Ψ. Wave functions are complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density of measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called normalization. Since the wave function is complex-valued, only its relative phase and relative magnitude can be measured; its value does not, in isolation, tell anything about the magnitudes or directions of measurable observables. One has to apply quantum operators, whose eigenvalues correspond to sets of possible results of measurements, to the wave function ψ and calculate the statistical distributions for measurable quantities.
In physics, an operator is a function over a space of physical states onto another space of physical states. The simplest example of the utility of operators is the study of symmetry. Because of this, they are useful tools in classical mechanics. Operators are even more important in quantum mechanics, where they form an intrinsic part of the formulation of the theory.

In quantum mechanics, a probability amplitude is a complex number used for describing the behaviour of systems. The square of the modulus of this quantity represents a probability density.

In physics, the Rabi cycle is the cyclic behaviour of a two-level quantum system in the presence of an oscillatory driving field. A great variety of physical processes belonging to the areas of quantum computing, condensed matter, atomic and molecular physics, and nuclear and particle physics can be conveniently studied in terms of two-level quantum mechanical systems, and exhibit Rabi flopping when coupled to an optical driving field. The effect is important in quantum optics, magnetic resonance and quantum computing, and is named after Isidor Isaac Rabi.

In physics, canonical quantization is a procedure for quantizing a classical theory, while attempting to preserve the formal structure, such as symmetries, of the classical theory to the greatest extent possible.
In quantum mechanics, a complete set of commuting observables (CSCO) is a set of commuting operators whose common eigenvectors can be used as a basis to express any quantum state. In the case of operators with discrete spectra, a CSCO is a set of commuting observables whose simultaneous eigenspaces span the Hilbert space, so that the eigenvectors are uniquely specified by the corresponding sets of eigenvalues.

In quantum mechanics, an energy level is degenerate if it corresponds to two or more different measurable states of a quantum system. Conversely, two or more different states of a quantum mechanical system are said to be degenerate if they give the same value of energy upon measurement. The number of different states corresponding to a particular energy level is known as the degree of degeneracy of the level. It is represented mathematically by the Hamiltonian for the system having more than one linearly independent eigenstate with the same energy eigenvalue. When this is the case, energy alone is not enough to characterize what state the system is in, and other quantum numbers are needed to characterize the exact state when distinction is desired. In classical mechanics, this can be understood in terms of different possible trajectories corresponding to the same energy.
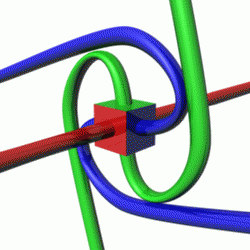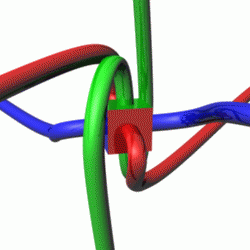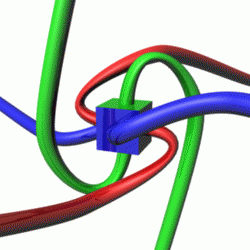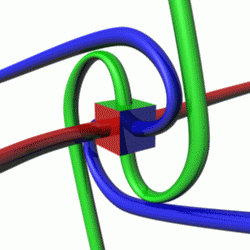
In quantum mechanics, spin is an intrinsic property of all elementary particles. All known fermions, the particles that constitute ordinary matter, have a spin of 1/2. The spin number describes how many symmetrical facets a particle has in one full rotation; a spin of 1/2 means that the particle must be rotated by two full turns before it has the same configuration as when it started.
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.
In quantum physics, unitarity is the condition that the time evolution of a quantum state according to the Schrödinger equation is mathematically represented by a unitary operator. This is typically taken as an axiom or basic postulate of quantum mechanics, while generalizations of or departures from unitarity are part of speculations about theories that may go beyond quantum mechanics. A unitarity bound is any inequality that follows from the unitarity of the evolution operator, i.e. from the statement that time evolution preserves inner products in Hilbert space.
In quantum mechanics, the eigenvalue of an observable is said to be a good quantum number if the observable is a constant of motion. In other words, the quantum number is good if the corresponding observable commutes with the Hamiltonian. If the system starts from the eigenstate with an eigenvalue , it remains on that state as the system evolves in time, and the measurement of always yields the same eigenvalue .
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a quantum-mechanical prediction for the system represented by the state. Knowledge of the quantum state, and the quantum mechanical rules for the system's evolution in time, exhausts all that can be known about a quantum system.
This is a glossary for the terminology often encountered in undergraduate quantum mechanics courses.
The eigenstate thermalization hypothesis is a set of ideas which purports to explain when and why an isolated quantum mechanical system can be accurately described using equilibrium statistical mechanics. In particular, it is devoted to understanding how systems which are initially prepared in far-from-equilibrium states can evolve in time to a state which appears to be in thermal equilibrium. The phrase "eigenstate thermalization" was first coined by Mark Srednicki in 1994, after similar ideas had been introduced by Josh Deutsch in 1991. The principal philosophy underlying the eigenstate thermalization hypothesis is that instead of explaining the ergodicity of a thermodynamic system through the mechanism of dynamical chaos, as is done in classical mechanics, one should instead examine the properties of matrix elements of observable quantities in individual energy eigenstates of the system.
Exact diagonalization (ED) is a numerical technique used in physics to determine the eigenstates and energy eigenvalues of a quantum Hamiltonian. In this technique, a Hamiltonian for a discrete, finite system is expressed in matrix form and diagonalized using a computer. Exact diagonalization is only feasible for systems with a few tens of particles, due to the exponential growth of the Hilbert space dimension with the size of the quantum system. It is frequently employed to study lattice models, including the Hubbard model, Ising model, Heisenberg model, t-J model, and SYK model.





















