In probability theory, the expected value is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would "expect" to get in reality.

In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the unit hyperbola. Also, similarly to how the derivatives of sin(t) and cos(t) are cos(t) and –sin(t) respectively, the derivatives of sinh(t) and cosh(t) are cosh(t) and +sinh(t) respectively.

A logistic function or logistic curve is a common S-shaped curve with the equation

A sigmoid function is any mathematical function whose graph has a characteristic S-shaped or sigmoid curve.
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equation constraints. It is named after the mathematician Joseph-Louis Lagrange.

In statistics, the logistic model is a statistical model that models the log-odds of an event as a linear combination of one or more independent variables. In regression analysis, logistic regression is estimating the parameters of a logistic model. Formally, in binary logistic regression there is a single binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable or a continuous variable. The corresponding probability of the value labeled "1" can vary between 0 and 1, hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odds scale is called a logit, from logistic unit, hence the alternative names. See § Background and § Definition for formal mathematics, and § Example for a worked example.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form

In mathematics, trigonometric integrals are a family of nonelementary integrals involving trigonometric functions.
In Vapnik–Chervonenkis theory, the Vapnik–Chervonenkis (VC) dimension is a measure of the size of a class of sets. The notion can be extended to classes of binary functions. It is defined as the cardinality of the largest set of points that the algorithm can shatter, which means the algorithm can always learn a perfect classifier for any labeling of at least one configuration of those data points. It was originally defined by Vladimir Vapnik and Alexey Chervonenkis.

In mathematics, a Green's function is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions.
An artificial neuron is a mathematical function conceived as a model of biological neurons in a neural network. Artificial neurons are the elementary units of artificial neural networks. The artificial neuron is a function that receives one or more inputs, applies weights to these inputs, and sums them to produce an output.

In functional analysis, a reproducing kernel Hilbert space (RKHS) is a Hilbert space of functions in which point evaluation is a continuous linear functional. Roughly speaking, this means that if two functions and in the RKHS are close in norm, i.e., is small, then and are also pointwise close, i.e., is small for all . The converse does not need to be true. Informally, this can be shown by looking at the supremum norm: the sequence of functions converges pointwise, but does not converge uniformly i.e. does not converge with respect to the supremum norm.
In machine learning, backpropagation is a gradient estimation method used to train neural network models. The gradient estimate is used by the optimization algorithm to compute the network parameter updates.
In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices. It collects the various partial derivatives of a single function with respect to many variables, and/or of a multivariate function with respect to a single variable, into vectors and matrices that can be treated as single entities. This greatly simplifies operations such as finding the maximum or minimum of a multivariate function and solving systems of differential equations. The notation used here is commonly used in statistics and engineering, while the tensor index notation is preferred in physics.
The softmax function, also known as softargmax or normalized exponential function, converts a vector of K real numbers into a probability distribution of K possible outcomes. It is a generalization of the logistic function to multiple dimensions, and used in multinomial logistic regression. The softmax function is often used as the last activation function of a neural network to normalize the output of a network to a probability distribution over predicted output classes.

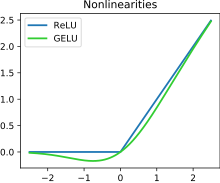
The activation function of a node in an artificial neural network is a function that calculates the output of the node based on its individual inputs and their weights. Nontrivial problems can be solved using only a few nodes if the activation function is nonlinear. Modern activation functions include the smooth version of the ReLU, the GELU, which was used in the 2018 BERT model, the logistic (sigmoid) function used in the 2012 speech recognition model developed by Hinton et al, the ReLU used in the 2012 AlexNet computer vision model and in the 2015 ResNet model.
In statistics, the variance function is a smooth function that depicts the variance of a random quantity as a function of its mean. The variance function is a measure of heteroscedasticity and plays a large role in many settings of statistical modelling. It is a main ingredient in the generalized linear model framework and a tool used in non-parametric regression, semiparametric regression and functional data analysis. In parametric modeling, variance functions take on a parametric form and explicitly describe the relationship between the variance and the mean of a random quantity. In a non-parametric setting, the variance function is assumed to be a smooth function.
In machine learning, the vanishing gradient problem is encountered when training neural networks with gradient-based learning methods and backpropagation. In such methods, during each iteration of training each of the neural networks weights receives an update proportional to the partial derivative of the error function with respect to the current weight. The problem is that as the sequence length increases, the gradient magnitude typically is expected to decrease, slowing the training process. In the worst case, this may completely stop the neural network from further training. As one example of the problem cause, traditional activation functions such as the hyperbolic tangent function have gradients in the range [-1,1], and backpropagation computes gradients by the chain rule. This has the effect of multiplying n of these small numbers to compute gradients of the early layers in an n-layer network, meaning that the gradient decreases exponentially with n while the early layers train very slowly.

The swish function is a mathematical function defined as follows: