Motivation
RLS was discovered by Gauss but lay unused or ignored until 1950 when Plackett rediscovered the original work of Gauss from 1821. In general, the RLS can be used to solve any problem that can be solved by adaptive filters. For example, suppose that a signal is transmitted over an echoey, noisy channel that causes it to be received as
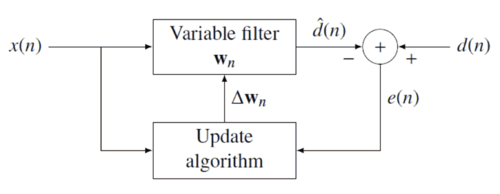
where represents additive noise. The intent of the RLS filter is to recover the desired signal by use of a -tap FIR filter, :
where is the column vector containing the most recent samples of . The estimate of the recovered desired signal is
The goal is to estimate the parameters of the filter , and at each time we refer to the current estimate as and the adapted least-squares estimate by . is also a column vector, as shown below, and the transpose, , is a row vector. The matrix product (which is the dot product of and ) is , a scalar. The estimate is "good" if is small in magnitude in some least squares sense.
As time evolves, it is desired to avoid completely redoing the least squares algorithm to find the new estimate for , in terms of .
The benefit of the RLS algorithm is that there is no need to invert matrices, thereby saving computational cost. Another advantage is that it provides intuition behind such results as the Kalman filter.