Smallest-circle problem

Last updated December 19, 2023

The smallest-circle problem (also known as minimum covering circle problem, bounding circle problem, least bounding circle problem, smallest enclosing circle problem) is a computational geometry problem of computing the smallest circle that contains all of a given set of points in the Euclidean plane. The corresponding problem in n-dimensional space, the smallest bounding sphere problem, is to compute the smallest n-sphere that contains all of a given set of points.^[1] The smallest-circle problem was initially proposed by the English mathematician James Joseph Sylvester in 1857.^[2]

The smallest-circle problem in the plane is an example of a facility location problem (the 1-center problem) in which the location of a new facility must be chosen to provide service to a number of customers, minimizing the farthest distance that any customer must travel to reach the new facility.^[3] Both the smallest circle problem in the plane, and the smallest bounding sphere problem in any higher-dimensional space of bounded dimension are solvable in worst-case linear time.

Characterization

Most of the geometric approaches for the problem look for points that lie on the boundary of the minimum circle and are based on the following simple facts:

The minimum covering circle is unique.
The minimum covering circle of a set S can be determined by at most three points in S which lie on the boundary of the circle. If it is determined by only two points, then the line segment joining those two points must be a diameter of the minimum circle. If it is determined by three points, then the triangle consisting of those three points is not obtuse.

Proof that the minimum covering disk is unique

Let P be any set of points in the plane, and suppose that there are two smallest enclosing disks of P, with centers at ${\vec {z}}_{1}$ and ${\vec {z}}_{2}$ . Let $r$ be their shared radius, and let $2a$ be the distance between their centers. Since P is a subset of both disks it is a subset of their intersection. However, their intersection is contained within the disk with center ${\frac {1}{2}}({\vec {z}}_{1}+{\vec {z}}_{2})$ and radius ${\sqrt {r^{2}-a^{2}}}$ , as shown in the following image:

Since r is minimal, we must have ${\sqrt {r^{2}-a^{2}}}=r$ , meaning $a=0$ , so the disks are identical.^[4]

Linear-time solutions

As Nimrod Megiddo showed,^[5] the minimum enclosing circle can be found in linear time, and the same linear time bound also applies to the smallest enclosing sphere in Euclidean spaces of any constant dimension. His article also gives a brief overview of earlier $O(n^{3})$ and $O(n\log n)$ algorithms;^[6] in doing so, Megiddo demonstrated that Shamos and Hoey's conjecture – that a solution to the smallest-circle problem was computable in $\Omega (n\log n)$ at best – was false.^[7]

Emo Welzl ^[8] proposed a simple randomized algorithm for the minimum covering circle problem that runs in expected time $O(n)$ , based on a linear programming algorithm of Raimund Seidel.

Subsequently, the smallest-circle problem was included in a general class of LP-type problems that can be solved by algorithms like Welzl's based on linear programming. As a consequence of membership in this class, it was shown that the dependence on the dimension of the constant factor in the $O(n)$ time bound, which was factorial for Seidel's method, could be reduced to subexponential.^[6]

Megiddo's algorithm

Megiddo's algorithm^[9] is based on the technique called prune and search, reducing the size of the problem by removing ${\textstyle {\frac {n}{16}}}$ unnecessary points. That leads to the recurrence $t(n)\leq t\left({\frac {15n}{16}}\right)+cn$ giving $t(n)=16cn$ .

The algorithm is rather complicated and it is reflected by its big multiplicative constant. The reduction needs to solve twice the similar problem where the center of the sought-after enclosing circle is constrained to lie on a given line. The solution of the subproblem is either the solution of the unconstrained problem or it is used to determine the half-plane where the unconstrained solution center is located.

The ${\textstyle {\frac {n}{16}}}$ points to be discarded are found as follows: The points P_i are arranged into pairs which defines ${\textstyle {\frac {n}{2}}}$ lines p_j as their bisectors. The median average p_m of bisectors in order by their directions (oriented to the same half-plane determined by bisector $p 1$ ) is found and pairs of bisectors are made, such that in each pair one bisector has direction at most p_m and the other at least p_m (direction $p 1$ could be considered as − $\infty$ or + $\infty$ according our needs.) Let Q_k be the intersection of the bisectors in the k-th pair.

The line q in the $p 1$ direction is placed to go through an intersection Q_x such that there are ${\textstyle {\frac {n}{8}}}$ intersections in each half-plane defined by the line (median position). The constrained version of the enclosing problem is run on the line q' which determines half-plane where the center is located. The line q′ in the p_m direction is placed to go through an intersection Q_x' such that there are ${\textstyle {\frac {n}{16}}}$ intersections in each half of the half-plane not containing the solution. The constrained version of the enclosing problem is run on line q′ which together with q determines the quadrant where the center is located. We consider the points Q_k in the quadrant not contained in a half-plane containing the solution. One of the bisectors of the pair defining Q_k has the direction ensuring which of points P_i defining the bisector is closer to each point in the quadrant containing the center of the enclosing circle. This point could be discarded.

The constrained version of the algorithm is also solved by the prune and search technique, but reducing the problem size by removal of ${\textstyle {\frac {n}{4}}}$ points leading to recurrence

t(n)\leq t\left({\frac {3n}{4}}\right)+cn

giving $t(n)=4cn$ .

The ${\textstyle {\frac {n}{4}}}$ points to be discarded are found as follows: Points P_i are arranged into pairs. For each pair, the intersection Q_j of its bisector with the constraining line q is found (If this intersection does not exist we could remove one point from the pair immediately). The median M of points Q_j on the line q is found and in O(n) time is determined which halfline of q starting in M contains the solution of the constrained problem. We consider points Q_j from the other half. We know which of the points P_i defining Q_j is closer to the each point of the halfline containing center of the enclosing circle of the constrained problem solution. This point could be discarded.

The half-plane where the unconstrained solution lies could be determined by the points P_i on the boundary of the constrained circle solution. (The first and last point on the circle in each half-plane suffice. If the center belongs to their convex hull, it is unconstrained solution, otherwise the direction to the nearest edge determines the half-plane of the unconstrained solution.)

Welzl's algorithm

The algorithm is recursive.

The initial input is a set P of points. The algorithm selects one point p randomly and uniformly from P, and recursively finds the minimal circle containing P – {p}, i.e. all of the other points in P except p. If the returned circle also encloses p, it is the minimal circle for the whole of P and is returned.

Otherwise, point p must lie on the boundary of the result circle. It recurses, but with the set R of points known to be on the boundary as an additional parameter.

The recursion terminates when P is empty, and a solution can be found from the points in R: for 0 or 1 points the solution is trivial, for 2 points the minimal circle has its center at the midpoint between the two points, and for 3 points the circle is the circumcircle of the triangle described by the points. (In three dimensions, 4 points require the calculation of the circumsphere of a tetrahedron.)

Recursion can also terminate when R has size 3 (in 2D, or 4 in 3D) because the remaining points in P must lie within the circle described by R.

algorithm welzl is^[8]input: Finite sets P and R of points in the plane |R| ≤ 3.     output: Minimal disk enclosing P with R on the boundary.      ifP is empty or |R| = 3 thenreturn trivial(R)     choosep in P (randomly and uniformly)     D := welzl(P − {p}, R)     ifp is in DthenreturnDreturn welzl(P − {p}, R ∪ {p})

Welzl's paper states that it is sufficient to randomly permute the input at the start, rather than performing independently random choices of p on each recursion.

It also states that performance is improved by dynamically re-ordering the points so that those that are found to be outside a circle are subsequently considered earlier, but this requires a change in the structure of the algorithm to store P as a "global".

Other algorithms

Prior to Megiddo's result showing that the smallest-circle problem may be solved in linear time, several algorithms of higher complexity appeared in the literature. A naive algorithm solves the problem in time O(n⁴) by testing the circles determined by all pairs and triples of points.

An algorithm of Chrystal and Peirce applies a local optimization strategy that maintains two points on the boundary of an enclosing circle and repeatedly shrinks the circle, replacing the pair of boundary points, until an optimal circle is found. Chakraborty and Chaudhuri^[10] propose a linear-time method for selecting a suitable initial circle and a pair of boundary points on that circle. Each step of the algorithm includes as one of the two boundary points a new vertex of the convex hull, so if the hull has h vertices this method can be implemented to run in time O(nh).
Elzinga and Hearn^[11] described an algorithm which maintains a covering circle for a subset of the points. At each step, a point not covered by the current sphere is used to find a larger sphere that covers a new subset of points, including the point found. Although its worst case running time is O(h³n), the authors report that it ran in linear time in their experiments. The complexity of the method has been analyzed by Drezner and Shelah.^[12] Both Fortran and C codes are available from Hearn, Vijay & Nickel (1995).^[13]
The smallest sphere problem can be formulated as a quadratic program ^[1] defined by a system of linear constraints with a convex quadratic objective function. Therefore, any feasible direction algorithm can give the solution of the problem.^[14] Hearn and Vijay^[15] proved that the feasible direction approach chosen by Jacobsen is equivalent to the Chrystal–Peirce algorithm.
The dual to this quadratic program may also be formulated explicitly;^[16] an algorithm of Lawson^[17] can be described in this way as a primal dual algorithm.^[15]
Shamos and Hoey^[7] proposed an O(n log n) time algorithm for the problem based on the observation that the center of the smallest enclosing circle must be a vertex of the farthest-point Voronoi diagram of the input point set.

Weighted variants of the problem

The weighted version of the minimum covering circle problem takes as input a set of points in a Euclidean space, each with weights; the goal is to find a single point that minimizes the maximum weighted distance (i.e., distance multiplied by the corresponding weight) to any point. The original (unweighted) minimum covering circle problem corresponds to the case when all weights are equal to 1. As with the unweighted problem, the weighted problem may be solved in linear time in any space of bounded dimension, using approaches closely related to bounded dimension linear programming algorithms, although slower algorithms are again frequent in the literature.^[15]^[18]^[19]

Related Research Articles

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.

<span class="mw-page-title-main">Circle</span> Simple curve of Euclidean geometry

A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius.

<span class="mw-page-title-main">Packing problems</span> Problems which attempt to find the most efficient way to pack objects into containers

Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real-life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.

An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints are linear.

<span class="mw-page-title-main">Concyclic points</span> Points on a common circle

In geometry, a set of points are said to be concyclic if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its circumscribing circle or circumcircle. All concyclic points are equidistant from the center of the circle.

In mathematical measure theory, for every positive integer $n$ the ham sandwich theorem states that given $n$ measurable "objects" in $n$ -dimensional Euclidean space, it is possible to divide each one of them in half (with respect to their measure, e.g. volume) with a single $(n - 1)$ -dimensional hyperplane. This is even possible if the objects overlap.

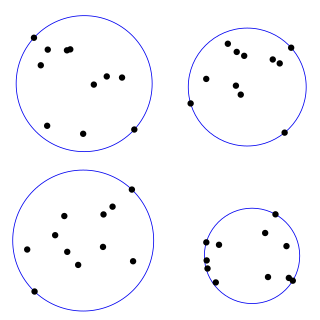
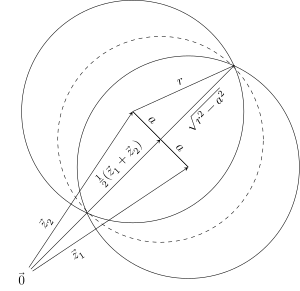
In mathematics, given a non-empty set of objects of finite extension in $-dimensional space, for example a set of points, a bounding sphere, enclosing sphere or enclosing ball for that set is a -dimensional solid sphere containing all of these objects.$

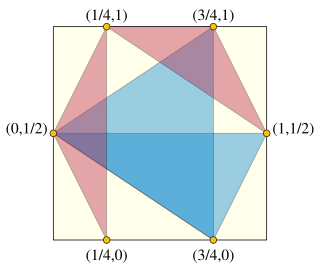
In discrete geometry and discrepancy theory, the Heilbronn triangle problem is a problem of placing points in the plane, avoiding triangles of small area. It is named after Hans Heilbronn, who conjectured that, no matter how points are placed in a given area, the smallest triangle area will be at most inversely proportional to the square of the number of points. His conjecture was proven false, but the asymptotic growth rate of the minimum triangle area remains unknown.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

<span class="mw-page-title-main">No-three-in-line problem</span> Geometry problem on grid points

The no-three-in-line problem in discrete geometry asks how many points can be placed in the $grid so that no three points lie on the same line. The problem concerns lines of all slopes, not only those aligned with the grid. It was introduced by Henry Dudeney in 1900. Brass, Moser, and Pach call it "one of the oldest and most extensively studied geometric questions concerning lattice points".$

In mathematics, the relaxation of a (mixed) integer linear program is the problem that arises by removing the integrality constraint of each variable.

<span class="mw-page-title-main">K-set (geometry)</span> Points separated from others by a line

In discrete geometry, a $-set of a finite point set in the Euclidean plane is a subset of elements of that can be strictly separated from the remaining points by a line. More generally, in Euclidean space of higher dimensions, a -set of a finite point set is a subset of elements that can be separated from the remaining points by a hyperplane. In particular, when, the line or hyperplane that separates a -set from the rest of is a halving line or halving plane .$

<span class="mw-page-title-main">Maximum cut</span> Problem of finding a maximum cut in a graph

For a graph, a maximum cut is a cut whose size is at least the size of any other cut. That is, it is a partition of the graph's vertices into two complementary sets $S$ and $T$ , such that the number of edges between $S$ and $T$ is as large as possible. Finding such a cut is known as the max-cut problem.

In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows:

Prune and search is a method of solving optimization problems suggested by Nimrod Megiddo in 1983.

In the study of algorithms, an LP-type problem is an optimization problem that shares certain properties with low-dimensional linear programs and that may be solved by similar algorithms. LP-type problems include many important optimization problems that are not themselves linear programs, such as the problem of finding the smallest circle containing a given set of planar points. They may be solved by a combination of randomized algorithms in an amount of time that is linear in the number of elements defining the problem, and subexponential in the dimension of the problem.

In discrete geometry, an opaque set is a system of curves or other set in the plane that blocks all lines of sight across a polygon, circle, or other shape. Opaque sets have also been called barriers, beam detectors, opaque covers, or opaque forests. Opaque sets were introduced by Stefan Mazurkiewicz in 1916, and the problem of minimizing their total length was posed by Frederick Bagemihl in 1959.

In computer science, an optimal binary search tree (Optimal BST), sometimes called a weight-balanced binary tree, is a binary search tree which provides the smallest possible search time (or expected search time) for a given sequence of accesses (or access probabilities). Optimal BSTs are generally divided into two types: static and dynamic.

In the design and analysis of algorithms for combinatorial optimization, parametric search is a technique invented by Nimrod Megiddo (1983) for transforming a decision algorithm into an optimization algorithm. It is frequently used for solving optimization problems in computational geometry.

In graph theory, the cutwidth of an undirected graph is the smallest integer $with the following property: there is an ordering of the vertices of the graph, such that every cut obtained by partitioning the vertices into earlier and later subsets of the ordering is crossed by at most edges. That is, if the vertices are numbered, then for every, the number of edges with and is at most .$

References

1 2 Elzinga, J.; Hearn, D. W. (1972), "The minimum covering sphere problem", Management Science , 19: 96–104, doi:10.1287/mnsc.19.1.96
↑ Sylvester, J. J. (1857), "A question in the geometry of situation", Quarterly Journal of Mathematics , 1: 79.
↑ Francis, R. L.; McGinnis, L. F.; White, J. A. (1992), Facility Layout and Location: An Analytical Approach (2nd ed.), Englewood Cliffs, N.J.: Prentice–Hall, Inc..
↑ Welzl 1991, p. 2.
↑ Megiddo, Nimrod (1983), "Linear-time algorithms for linear programming in $R 3$ and related problems", SIAM Journal on Computing , 12 (4): 759–776, doi:10.1137/0212052, MR 0721011, S2CID 14467740 .
1 2 Matoušek, Jiří; Sharir, Micha; Welzl, Emo (1996), "A subexponential bound for linear programming" (PDF), Algorithmica , 16 (4–5): 498–516, CiteSeerX 10.1.1.46.5644 , doi:10.1007/BF01940877, S2CID 877032 .
1 2 Shamos, M. I.; Hoey, D. (1975), "Closest point problems", Proceedings of 16th Annual IEEE Symposium on Foundations of Computer Science, pp. 151–162, doi:10.1109/SFCS.1975.8, S2CID 40615455
1 2 Welzl, Emo (1991), "Smallest enclosing disks (balls and ellipsoids)", in Maurer, H. (ed.), New Results and New Trends in Computer Science, Lecture Notes in Computer Science, vol. 555, Springer-Verlag, pp. 359–370, CiteSeerX 10.1.1.46.1450 , doi:10.1007/BFb0038202, ISBN 978-3-540-54869-0 .
↑ Megiddo, Nimrod (1983), "Linear-time algorithms for linear programming in $R 3$ and related problems", SIAM Journal on Computing , 12 (4): 759–776, doi:10.1137/0212052, MR 0721011, S2CID 14467740 .
↑ Chakraborty, R. K.; Chaudhuri, P. K. (1981), "Note on geometrical solutions for some minimax location problems", Transportation Science , 15 (2): 164–166, doi: 10.1287/trsc.15.2.164 .
↑ Elzinga, J.; Hearn, D. W. (1972), "Geometrical solutions for some minimax location problems", Transportation Science , 6 (4): 379–394, doi:10.1287/trsc.6.4.379 .
↑ Drezner, Zvi; Shelah, Saharon (1987), "On the complexity of the Elzinga–Hearn algorithm for the 1-center problem", Mathematics of Operations Research , 12 (2): 255–261, doi:10.1287/moor.12.2.255, JSTOR 3689688 .
↑ Hearn, D. W.; Vijay, J.; Nickel, S. (1995), "Codes of geometrical algorithms for the (weighted) minimum circle problem", European Journal of Operational Research, 80: 236–237, doi:10.1016/0377-2217(95)90075-6 .
↑ Jacobsen, S. K. (1981), "An algorithm for the minimax Weber problem", European Journal of Operational Research, 6 (2): 144–148, doi:10.1016/0377-2217(81)90200-9 .
1 2 3 Hearn, D. W.; Vijay, J. (1982), "Efficient algorithms for the (weighted) minimum circle problem", Operations Research , 30 (4): 777–795, doi:10.1287/opre.30.4.777 .
↑ Elzinga, J.; Hearn, D. W.; Randolph, W. D. (1976), "Minimax multifacility location with Euclidean distances", Transportation Science , 10 (4): 321–336, doi:10.1287/trsc.10.4.321 .
↑ Lawson, C. L. (1965), "The smallest covering cone or sphere", SIAM Review , 7 (3): 415–417, doi:10.1137/1007084 .
↑ Megiddo, N. (1983), "The weighted Euclidean 1-center problem", Mathematics of Operations Research , 8 (4): 498–504, doi:10.1287/moor.8.4.498 .
↑ Megiddo, N.; Zemel, E. (1986), "An O(n log n) randomizing algorithm for the weighted Euclidean 1-center problem", Journal of Algorithms, 7 (3): 358–368, doi:10.1016/0196-6774(86)90027-1 .

External links

Bernd Gärtner's smallest enclosing ball code
CGAL the Min_sphere_of_spheres package of the Computational Geometry Algorithms Library (CGAL)
Miniball an open-source implementation of an algorithm for the smallest enclosing ball problem for low and moderately high dimensions

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[eh-mcsp-72-1] 1 2 Elzinga, J.; Hearn, D. W. (1972), "The minimum covering sphere problem", Management Science , 19: 96–104, doi:10.1287/mnsc.19.1.96

[2] Sylvester, J. J. (1857), "A question in the geometry of situation", Quarterly Journal of Mathematics , 1: 79.

[3] Francis, R. L.; McGinnis, L. F.; White, J. A. (1992), Facility Layout and Location: An Analytical Approach (2nd ed.), Englewood Cliffs, N.J.: Prentice–Hall, Inc..

[FOOTNOTEWelzl19912-4] Welzl 1991, p. 2.

[5] Megiddo, Nimrod (1983), "Linear-time algorithms for linear programming in $R 3$ and related problems", SIAM Journal on Computing , 12 (4): 759–776, doi:10.1137/0212052, MR 0721011, S2CID 14467740 .

[msw-6] 1 2 Matoušek, Jiří; Sharir, Micha; Welzl, Emo (1996), "A subexponential bound for linear programming" (PDF), Algorithmica , 16 (4–5): 498–516, CiteSeerX 10.1.1.46.5644 , doi:10.1007/BF01940877, S2CID 877032 .

[shamoshoey-7] 1 2 Shamos, M. I.; Hoey, D. (1975), "Closest point problems", Proceedings of 16th Annual IEEE Symposium on Foundations of Computer Science, pp. 151–162, doi:10.1109/SFCS.1975.8, S2CID 40615455

[Welzl_1991_359–370-8] 1 2 Welzl, Emo (1991), "Smallest enclosing disks (balls and ellipsoids)", in Maurer, H. (ed.), New Results and New Trends in Computer Science, Lecture Notes in Computer Science, vol. 555, Springer-Verlag, pp. 359–370, CiteSeerX 10.1.1.46.1450 , doi:10.1007/BFb0038202, ISBN 978-3-540-54869-0 .

[9] Megiddo, Nimrod (1983), "Linear-time algorithms for linear programming in $R 3$ and related problems", SIAM Journal on Computing , 12 (4): 759–776, doi:10.1137/0212052, MR 0721011, S2CID 14467740 .

[10] Chakraborty, R. K.; Chaudhuri, P. K. (1981), "Note on geometrical solutions for some minimax location problems", Transportation Science , 15 (2): 164–166, doi: 10.1287/trsc.15.2.164 .

[11] Elzinga, J.; Hearn, D. W. (1972), "Geometrical solutions for some minimax location problems", Transportation Science , 6 (4): 379–394, doi:10.1287/trsc.6.4.379 .

[12] Drezner, Zvi; Shelah, Saharon (1987), "On the complexity of the Elzinga–Hearn algorithm for the 1-center problem", Mathematics of Operations Research , 12 (2): 255–261, doi:10.1287/moor.12.2.255, JSTOR 3689688 .

[13] Hearn, D. W.; Vijay, J.; Nickel, S. (1995), "Codes of geometrical algorithms for the (weighted) minimum circle problem", European Journal of Operational Research, 80: 236–237, doi:10.1016/0377-2217(95)90075-6 .

[14] Jacobsen, S. K. (1981), "An algorithm for the minimax Weber problem", European Journal of Operational Research, 6 (2): 144–148, doi:10.1016/0377-2217(81)90200-9 .

[hv-eawmcp-82-15] 1 2 3 Hearn, D. W.; Vijay, J. (1982), "Efficient algorithms for the (weighted) minimum circle problem", Operations Research , 30 (4): 777–795, doi:10.1287/opre.30.4.777 .

[16] Elzinga, J.; Hearn, D. W.; Randolph, W. D. (1976), "Minimax multifacility location with Euclidean distances", Transportation Science , 10 (4): 321–336, doi:10.1287/trsc.10.4.321 .

[17] Lawson, C. L. (1965), "The smallest covering cone or sphere", SIAM Review , 7 (3): 415–417, doi:10.1137/1007084 .

[18] Megiddo, N. (1983), "The weighted Euclidean 1-center problem", Mathematics of Operations Research , 8 (4): 498–504, doi:10.1287/moor.8.4.498 .

[19] Megiddo, N.; Zemel, E. (1986), "An O(n log n) randomizing algorithm for the weighted Euclidean 1-center problem", Journal of Algorithms, 7 (3): 358–368, doi:10.1016/0196-6774(86)90027-1 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]