Related Research Articles

In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a general position is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.

In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.

In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. In the simplest case, these objects are just finitely many points in the plane. For each seed there is a corresponding region, called a Voronoi cell, consisting of all points of the plane closer to that seed than to any other. The Voronoi diagram of a set of points is dual to that set's Delaunay triangulation.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.
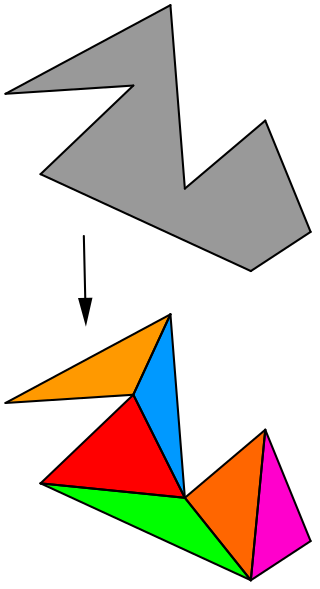
In computational geometry, polygon triangulation is the partition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

A triangulation of a set of points in the Euclidean space is a simplicial complex that covers the convex hull of , and whose vertices belong to . In the plane, triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of are vertices of its triangulations. In this case, a triangulation of a set of points in the plane can alternatively be defined as a maximal set of non-crossing edges between points of . In the plane, triangulations are special cases of planar straight-line graphs.
In geometry, a triangulation is a subdivision of a planar object into triangles, and by extension the subdivision of a higher-dimension geometric object into simplices. Triangulations of a three-dimensional volume would involve subdividing it into tetrahedra packed together.

In computational geometry, a sweep line algorithm or plane sweep algorithm is an algorithmic paradigm that uses a conceptual sweep line or sweep surface to solve various problems in Euclidean space. It is one of the critical techniques in computational geometry.
Proximity problems is a class of problems in computational geometry which involve estimation of distances between geometric objects.
In computational geometry, the Bowyer–Watson algorithm is a method for computing the Delaunay triangulation of a finite set of points in any number of dimensions. The algorithm can be also used to obtain a Voronoi diagram of the points, which is the dual graph of the Delaunay triangulation.
The dynamic convex hull problem is a class of dynamic problems in computational geometry. The problem consists in the maintenance, i.e., keeping track, of the convex hull for input data undergoing a sequence of discrete changes, i.e., when input data elements may be inserted, deleted, or modified. It should be distinguished from the kinetic convex hull, which studies similar problems for continuously moving points. Dynamic convex hull problems may be distinguished by the types of the input data and the allowed types of modification of the input data.
Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science.
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.
In computational geometry, a constrained Delaunay triangulation is a generalization of the Delaunay triangulation that forces certain required segments into the triangulation as edges, unlike the Delaunay triangulation itself which is based purely on the position of a given set of vertices without regard to how they should be connected by edges. It can be computed efficiently and has applications in geographic information systems and in mesh generation.
Reverse-search algorithms are a class of algorithms for generating all objects of a given size, from certain classes of combinatorial objects. In many cases, these methods allow the objects to be generated in polynomial time per object, using only enough memory to store a constant number of objects. They work by organizing the objects to be generated into a spanning tree of their state space, and then performing a depth-first search of this tree.
References
- ↑ Franco P. Preparata and Michael Ian Shamos (1985). Computational Geometry - An Introduction. Springer-Verlag. ISBN 0-387-96131-3. 1st edition; 2nd printing, corrected and expanded, 1988.
- ↑ A.R. Forrest, "Computational geometry", Proc. Royal Society London, 321, series 4, 187-195 (1971)
- ↑ Yevgeny B. Karasik (2019). Optical Computational Geometry. ISBN 979-8511243344.
- ↑ S. Khuller and Y. Matias. A simple randomized sieve algorithm for the closest-pair problem. Inf. Comput., 118(1):34—37,1995 (PDF)
- ↑ S. Fortune and J.E. Hopcroft. "A note on Rabin's nearest-neighbor algorithm." Information Processing Letters, 8(1), pp. 20—23, 1979
