Point in polygon

Last updated December 11, 2023

In computational geometry, the point-in-polygon (PIP) problem asks whether a given point in the plane lies inside, outside, or on the boundary of a polygon. It is a special case of point location problems and finds applications in areas that deal with processing geometrical data, such as computer graphics, computer vision, geographic information systems (GIS), motion planning, and computer-aided design (CAD).

Ray casting algorithm

The number of intersections for a ray passing from the exterior of the polygon to any point: If odd, it shows that the point lies inside the polygon; if even, the point lies outside the polygon. This test also works in three dimensions. RecursiveEvenPolygon.svg — The number of intersections for a ray passing from the exterior of the polygon to any point: If odd, it shows that the point lies inside the polygon; if even, the point lies outside the polygon. This test also works in three dimensions.

One simple way of finding whether the point is inside or outside a simple polygon is to test how many times a ray, starting from the point and going in any fixed direction, intersects the edges of the polygon. If the point is on the outside of the polygon the ray will intersect its edge an even number of times. If the point is on the inside of the polygon then it will intersect the edge an odd number of times. The status of a point on the edge of the polygon depends on the details of the ray intersection algorithm.

This algorithm is sometimes also known as the crossing number algorithm or the even–odd rule algorithm, and was known as early as 1962.^[3] The algorithm is based on a simple observation that if a point moves along a ray from infinity to the probe point and if it crosses the boundary of a polygon, possibly several times, then it alternately goes from the outside to inside, then from the inside to the outside, etc. As a result, after every two "border crossings" the moving point goes outside. This observation may be mathematically proved using the Jordan curve theorem.

Limited precision

If implemented on a computer with finite precision arithmetics, the results may be incorrect if the point lies very close to that boundary, because of rounding errors. For some applications, like video games or other entertainment products, this is not a large concern since they often favor speed over precision. However, for a formally correct computer program, one would have to introduce a numerical tolerance ε and test in line whether P (the point) lies within ε of L (the Line), in which case the algorithm should stop and report "P lies very close to the boundary."

Most implementations of the ray casting algorithm consecutively check intersections of a ray with all sides of the polygon in turn. In this case the following problem must be addressed. If the ray passes exactly through a vertex of a polygon, then it will intersect 2 segments at their endpoints. While it is OK for the case of the topmost vertex in the example or the vertex between crossing 4 and 5, the case of the rightmost vertex (in the example) requires that we count one intersection for the algorithm to work correctly. A similar problem arises with horizontal segments that happen to fall on the ray. The issue is solved as follows: If the intersection point is a vertex of a tested polygon side, then the intersection counts only if the other vertex of the side lies below the ray. This is effectively equivalent to considering vertices on the ray as lying slightly above the ray.

Once again, the case of the ray passing through a vertex may pose numerical problems in finite precision arithmetics: for two sides adjacent to the same vertex the straightforward computation of the intersection with a ray may not give the vertex in both cases. If the polygon is specified by its vertices, then this problem is eliminated by checking the y-coordinates of the ray and the ends of the tested polygon side before actual computation of the intersection. In other cases, when polygon sides are computed from other types of data, other tricks must be applied for the numerical robustness of the algorithm.

Winding number algorithm

Another technique used to check if a point is inside a polygon is to compute the given point's winding number with respect to the polygon. If the winding number is non-zero, the point lies inside the polygon. This algorithm is sometimes also known as the nonzero-rule algorithm.

One way to compute the winding number is to sum up the angles subtended by each side of the polygon.^[4] However, this involves costly inverse trigonometric functions, which generally makes this algorithm performance-inefficient (slower) compared to the ray casting algorithm. Luckily, these inverse trigonometric functions do not need to be computed. Since the result, the sum of all angles, can add up to 0 or $2\pi$ (or multiples of $2\pi$ ) only, it is sufficient to track through which quadrants the polygon winds,^[5] as it turns around the test point, which makes the winding number algorithm comparable in speed to counting the boundary crossings.

An improved algorithm to calculate the winding number was developed by Dan Sunday in 2001.^[6] It does not use angles in calculations, nor any trigonometry, and functions exactly the same as the ray casting algorithms described above. Sunday's algorithm works by considering an infinite horizontal ray cast from the point being checked. Whenever that ray crosses an edge of the polygon, Juan Pineda's edge crossing algorithm (1988)^[7] is used to determine how the crossing will affect the winding number. As Sunday describes it, if the edge crosses the ray going "upwards", the winding number is incremented; if it crosses the ray "downwards", the number is decremented. Sunday's algorithm gives the correct answer for nonsimple polygons, whereas the boundary crossing algorithm fails in this case.^[6]

Implementations

SVG

Similar methods are used in SVG for defining a way of filling with color various shapes (such as path, polyline, polygon, text etc.).^[8] The algorithm of filling is influenced by 'fill-rule' attribute. The value may be either nonzero or evenodd. For example, in a pentagram, there is a central "hole" (visible background) with evenodd, and none with nonzero attribute.^[9]

For simple polygons, the algorithms will give the same result. However, for complex polygons, the algorithms may give different results for points in the regions where the polygon intersects itself, where the polygon does not have a clearly defined inside and outside. One solution using the even-odd rule is to transform (complex) polygons into simpler ones that are even-odd-equivalent before the intersection check.^[10] This, however, is computationally expensive. It is less expensive to use the fast non-zero winding number algorithm, which gives the correct result even when the polygon overlaps itself.

Point in polygon queries

The point in polygon problem may be considered in the general repeated geometric query setting: given a single polygon and a sequence of query points, quickly find the answers for each query point. Clearly, any of the general approaches for planar point location may be used. Simpler solutions are available for some special polygons.

Special cases

Simpler algorithms are possible for monotone polygons, star-shaped polygons, convex polygons and triangles.

The triangle case can be solved easily by use of a barycentric coordinate system, parametric equation or dot product.^[11] The dot product method extends naturally to any convex polygon.

Related Research Articles

In geometry, a polygon is a plane figure made up of line segments connected to form a closed polygonal chain.

Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.

Ray casting is the methodological basis for 3D CAD/CAM solid modeling and image rendering. It is essentially the same as ray tracing for computer graphics where virtual light rays are "cast" or "traced" on their path from the focal point of a camera through each pixel in the camera sensor to determine what is visible along the ray in the 3D scene. The term "Ray Casting" was introduced by Scott Roth while at the General Motors Research Labs from 1978–1980. His paper, "Ray Casting for Modeling Solids", describes modeled solid objects by combining primitive solids, such as blocks and cylinders, using the set operators union (+), intersection (&), and difference (-). The general idea of using these binary operators for solid modeling is largely due to Voelcker and Requicha's geometric modelling group at the University of Rochester. See solid modeling for a broad overview of solid modeling methods. This figure on the right shows a U-Joint modeled from cylinders and blocks in a binary tree using Roth's ray casting system in 1979.

The point location problem is a fundamental topic of computational geometry. It finds applications in areas that deal with processing geometrical data: computer graphics, geographic information systems (GIS), motion planning, and computer aided design (CAD).

<span class="mw-page-title-main">Bounding volume</span> Closed volume that completely contains the union of a set of objects

In computer graphics and computational geometry, a bounding volume for a set of objects is a closed region that completely contains the union of the objects in the set. Bounding volumes are used to improve the efficiency of geometrical operations, such as by using simple regions, having simpler ways to test for overlap.

<span class="mw-page-title-main">Convex polygon</span> Polygon that is the boundary of a convex set

In geometry, a convex polygon is a polygon that is the boundary of a convex set. This means that the line segment between two points of the polygon is contained in the union of the interior and the boundary of the polygon. In particular, it is a simple polygon. Equivalently, a polygon is convex if every line that does not contain any edge intersects the polygon in at most two points.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.

<span class="mw-page-title-main">Convex polytope</span> Convex hull of a finite set of points in a Euclidean space

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the $-dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.$

In computer graphics, line clipping is the process of removing (clipping) lines or portions of lines outside an area of interest. Typically, any part of a line which is outside of the viewing area is removed.

<span class="mw-page-title-main">Geometry processing</span>

Geometry processing, or mesh processing, is an area of research that uses concepts from applied mathematics, computer science and engineering to design efficient algorithms for the acquisition, reconstruction, analysis, manipulation, simulation and transmission of complex 3D models. As the name implies, many of the concepts, data structures, and algorithms are directly analogous to signal processing and image processing. For example, where image smoothing might convolve an intensity signal with a blur kernel formed using the Laplace operator, geometric smoothing might be achieved by convolving a surface geometry with a blur kernel formed using the Laplace-Beltrami operator.

<span class="mw-page-title-main">Straight skeleton</span> Method in geometry for representing a polygon by a topological skeleton

In geometry, a straight skeleton is a method of representing a polygon by a topological skeleton. It is similar in some ways to the medial axis but differs in that the skeleton is composed of straight line segments, while the medial axis of a polygon may involve parabolic curves. However, both are homotopy-equivalent to the underlying polygon.

The even–odd rule is an algorithm implemented in vector-based graphic software, like the PostScript language and Scalable Vector Graphics (SVG), which determines how a graphical shape with more than one closed outline will be filled. Unlike the nonzero-rule algorithm, this algorithm will alternatively color and leave uncolored shapes defined by nested closed paths irrespective of their winding.

<span class="mw-page-title-main">Pseudotriangle</span>

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.

The Sutherland–Hodgman algorithm is an algorithm used for clipping polygons. It works by extending each line of the convex clip polygon in turn and selecting only vertices from the subject polygon that are on the visible side.

In geometry, a vertex is a point where two or more curves, lines, or edges meet or intersect. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.

Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science.

In computational geometry, the visibility polygon or visibility region for a point $p$ in the plane among obstacles is the possibly unbounded polygonal region of all points of the plane visible from $p$ . The visibility polygon can also be defined for visibility from a segment, or a polygon. Visibility polygons are useful in robotics, video games, and in various optimization problems such as the facility location problem and the art gallery problem.

<span class="mw-page-title-main">Polygonal chain</span> Connected series of line segments

In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain $is a curve specified by a sequence of points called its vertices. The curve itself consists of the line segments connecting the consecutive vertices.$

The Greiner-Hormann algorithm is used in computer graphics for polygon clipping. It performs better than the Vatti clipping algorithm, but cannot handle degeneracies. It can process both self-intersecting and non-convex polygons. It can be trivially generalized to compute other Boolean operations on polygons, such as union and difference.

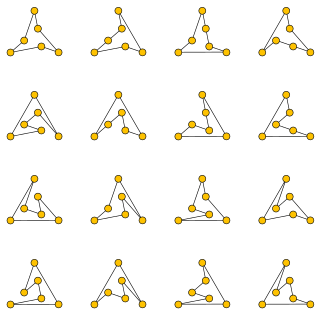
In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.

References

↑ Ivan Sutherland et al.,"A Characterization of Ten Hidden-Surface Algorithms" 1974, ACM Computing Surveys vol. 6 no. 1.
↑ "Point in Polygon, One More Time..." Archived 2018-05-24 at the Wayback Machine , Ray Tracing News , vol. 3 no. 4, October 1, 1990.
↑ Shimrat, M., "Algorithm 112: Position of point relative to polygon" 1962, Communications of the ACM Volume 5 Issue 8, Aug. 1962. https://dl.acm.org/doi/10.1145/368637.368653
↑ Hormann, K.; Agathos, A. (2001). "The point in polygon problem for arbitrary polygons". Computational Geometry. 20 (3): 131. doi: 10.1016/S0925-7721(01)00012-8 .
↑ Weiler, Kevin (1994), "An Incremental Angle Point in Polygon Test", in Heckbert, Paul S. (ed.), Graphics Gems IV, San Diego, CA, USA: Academic Press Professional, Inc., pp. 16–23, ISBN 0-12-336155-9
1 2 Sunday, Dan (2001). "Inclusion of a Point in a Polygon". Archived from the original on 26 January 2013.
↑ Pineda, Juan (August 1988). A Parallel Algorithm for Polygon Rasterization (PDF). SIGGRAPH'88. Computer Graphics. Vol. 22, no. 4. Atlanta . Retrieved 8 August 2021.
↑ "Painting: Filling, Stroking, Colors and Paint Servers – SVG Tiny 1.2". www.w3.org. Retrieved 2021-07-24.
↑ "Painting: Filling, Stroking, Colors and Paint Servers – SVG Tiny 1.2". www.w3.org. Retrieved 2021-07-24.
↑ Michael Galetzka, Patrick Glauner (2017). A Simple and Correct Even-Odd Algorithm for the Point-in-Polygon Problem for Complex Polygons. Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), Volume 1: GRAPP.
↑ Accurate point in triangle test "...the most famous methods to solve it"