Discrete-event simulation
In order to determine the next event in a stochastic simulation, the rates of all possible changes to the state of the model are computed, and then ordered in an array. Next, the cumulative sum of the array is taken, and the final cell contains the number R, where R is the total event rate. This cumulative array is now a discrete cumulative distribution, and can be used to choose the next event by picking a random number z~U(0,R) and choosing the first event, such that z is less than the rate associated with that event.
Probability distributions
A probability distribution is used to describe the potential outcome of a random variable.
Limits the outcomes where the variable can only take on discrete values. [4]
Bernoulli distribution
A random variable X is Bernoulli-distributed with parameter p if it has two possible outcomes usually encoded 1 (success or default) or 0 (failure or survival) [5] where the probabilities of success and failure are and where .
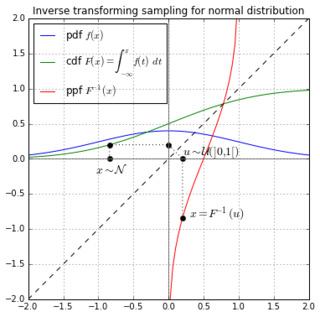
To produce a random variable X with a Bernoulli distribution from a U(0,1) uniform distribution made by a random number generator, we define
such that the probability for and . [2]
Example: Toss of coin
Define
For a fair coin, both realizations are equally likely. We can generate realizations of this random variable X from a uniform distribution provided by a random number generator (RNG) by having if the RNG outputs a value between 0 and 0.5 and if the RNG outputs a value between 0.5 and 1.
Of course, the two outcomes may not be equally likely (e.g. success of medical treatment). [6]
Binomial distribution
A binomial distributed random variable Y with parameters n and p is obtained as the sum of n independent and identically Bernoulli-distributed random variables X1, X2, ..., Xn [4]
Example: A coin is tossed three times. Find the probability of getting exactly two heads. This problem can be solved by looking at the sample space. There are three ways to get two heads.
The answer is 3/8 (= 0.375). [7]
Poisson distribution
A poisson process is a process where events occur randomly in an interval of time or space. [2] [8] The probability distribution for Poisson processes with constant rate λ per time interval is given by the following equation. [4]
Defining as the number of events that occur in the time interval
It can be shown that inter-arrival times for events is exponentially distributed with a cumulative distribution function (CDF) of . The inverse of the exponential CDF is given by
where is an uniformly distributed random variable. [2]
Simulating a Poisson process with a constant rate for the number of events that occur in interval can be carried out with the following algorithm. [9]
- Begin with and
- Generate random variable from uniform distribution
- Update the time with
- If , then stop. Else continue to step 5.
- Continue to step 2
Methods
Direct and first reaction methods
Published by Dan Gillespie in 1977, and is a linear search on the cumulative array. See Gillespie algorithm.
Gillespie’s Stochastic Simulation Algorithm (SSA) is essentially an exact procedure for numerically simulating the time evolution of a well-stirred chemically reacting system by taking proper account of the randomness inherent in such a system. [10]
It is rigorously based on the same microphysical premise that underlies the chemical master equation and gives a more realistic representation of a system’s evolution than the deterministic reaction rate equation (RRE) represented mathematically by ODEs. [10]
As with the chemical master equation, the SSA converges, in the limit of large numbers of reactants, to the same solution as the law of mass action.
Next reaction method
Published 2000 by Gibson and Bruck. [11] This is an improvement over the first reaction method where the unused reaction times are reused. To make the sampling of reactions more efficient, an indexed priority queue is used to store the reaction times. On the other hand, to make the recomputation of propensities more efficient, a dependency graph is used. This dependency graph tells which reaction propensities to update after a particular reaction has fired.
Optimised and sorting direct methods
Published 2004 [12] and 2005. These methods sort the cumulative array to reduce the average search depth of the algorithm. The former runs a presimulation to estimate the firing frequency of reactions, whereas the latter sorts the cumulative array on-the-fly.
Logarithmic direct method
Published in 2006. This is a binary search on the cumulative array, thus reducing the worst-case time complexity of reaction sampling to O (log M).
Partial-propensity methods
Published in 2009, 2010, and 2011 (Ramaswamy 2009, 2010, 2011). Use factored-out, partial reaction propensities to reduce the computational cost to scale with the number of species in the network, rather than the (larger) number of reactions. Four variants exist:
- PDM, the partial-propensity direct method. Has a computational cost that scales linearly with the number of different species in the reaction network, independent of the coupling class of the network (Ramaswamy 2009).
- SPDM, the sorting partial-propensity direct method. Uses dynamic bubble sort to reduce the pre-factor of the computational cost in multi-scale reaction networks where the reaction rates span several orders of magnitude (Ramaswamy 2009).
- PSSA-CR, the partial-propensity SSA with composition-rejection sampling. Reduces the computational cost to constant time (i.e., independent of network size) for weakly coupled networks (Ramaswamy 2010) using composition-rejection sampling (Slepoy 2008).
- dPDM, the delay partial-propensity direct method. Extends PDM to reaction networks that incur time delays (Ramaswamy 2011) by providing a partial-propensity variant of the delay-SSA method (Bratsun 2005, Cai 2007).
The use of partial-propensity methods is limited to elementary chemical reactions, i.e., reactions with at most two different reactants. Every non-elementary chemical reaction can be equivalently decomposed into a set of elementary ones, at the expense of a linear (in the order of the reaction) increase in network size.
Approximate Methods
A general drawback of stochastic simulations is that for big systems, too many events happen which cannot all be taken into account in a simulation. The following methods can dramatically improve simulation speed by some approximations.
τ leaping method
Since the SSA method keeps track of each transition, it would be impractical to implement for certain applications due to high time complexity. Gillespie proposed an approximation procedure, the tau-leaping method which decreases computational time with minimal loss of accuracy. [13] Instead of taking incremental steps in time, keeping track of X(t) at each time step as in the SSA method, the tau-leaping method leaps from one subinterval to the next, approximating how many transitions take place during a given subinterval. It is assumed that the value of the leap, τ, is small enough that there is no significant change in the value of the transition rates along the subinterval [t, t + τ]. This condition is known as the leap condition. The tau-leaping method thus has the advantage of simulating many transitions in one leap while not losing significant accuracy, resulting in a speed up in computational time. [14]
Conditional Difference Method
This method approximates reversible processes (which includes random walk/diffusion processes) by taking only net rates of the opposing events of a reversible process into account. The main advantage of this method is that it can be implemented with a simple if-statement replacing the previous transition rates of the model with new, effective rates. The model with the replaced transition rates can thus be solved, for instance, with the conventional SSA. [15]