
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.
A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic or procedure. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random determined by the random bits; thus either the running time, or the output are random variables.

In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set of vertices such that for every two vertices in , there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in . A set is independent if and only if it is a clique in the graph's complement. The size of an independent set is the number of vertices it contains. Independent sets have also been called "internally stable sets", of which "stable set" is a shortening.
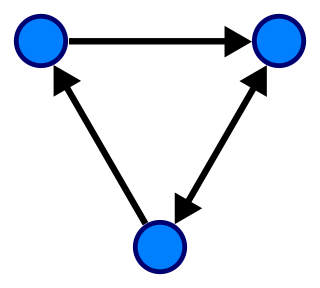
In computer science, a graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from the field of graph theory within mathematics.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.
A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.

In graph theory, a random geometric graph (RGG) is the mathematically simplest spatial network, namely an undirected graph constructed by randomly placing N nodes in some metric space and connecting two nodes by a link if and only if their distance is in a given range, e.g. smaller than a certain neighborhood radius, r.
In theoretical computer science, the Aanderaa–Karp–Rosenberg conjecture is a group of related conjectures about the number of questions of the form "Is there an edge between vertex and vertex ?" that have to be answered to determine whether or not an undirected graph has a particular property such as planarity or bipartiteness. They are named after Stål Aanderaa, Richard M. Karp, and Arnold L. Rosenberg. According to the conjecture, for a wide class of properties, no algorithm can guarantee that it will be able to skip any questions: any algorithm for determining whether the graph has the property, no matter how clever, might need to examine every pair of vertices before it can give its answer. A property satisfying this conjecture is called evasive.
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.
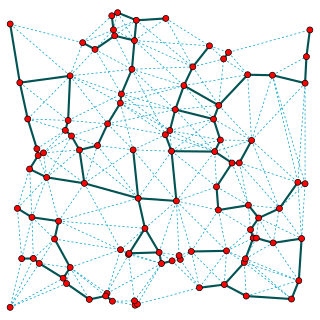
In computational geometry and geometric graph theory, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.
In the mathematical field of graph theory, the intersection number of a graph is the smallest number of elements in a representation of as an intersection graph of finite sets. In such a representation, each vertex is represented as a set, and two vertices are connected by an edge whenever their sets have a common element. Equivalently, the intersection number is the smallest number of cliques needed to cover all of the edges of .

In computational geometry, the Yao graph, named after Andrew Yao, is a kind of geometric spanner, a weighted undirected graph connecting a set of geometric points with the property that, for every pair of points in the graph, their shortest path has a length that is within a constant factor of their Euclidean distance.

A hyperbolic geometric graph (HGG) or hyperbolic geometric network (HGN) is a special type of spatial network where (1) latent coordinates of nodes are sprinkled according to a probability density function into a hyperbolic space of constant negative curvature and (2) an edge between two nodes is present if they are close according to a function of the metric (typically either a Heaviside step function resulting in deterministic connections between vertices closer than a certain threshold distance, or a decaying function of hyperbolic distance yielding the connection probability). A HGG generalizes a random geometric graph (RGG) whose embedding space is Euclidean.
The k-semi-Yao graph (k-SYG) of a set of n objects P is a geometric proximity graph, which was first described to present a kinetic data structure for maintenance of all the nearest neighbors on moving objects. It is named for its relation to the Yao graph, which is named after Andrew Yao.
In geometry, a partition of a polygon is a set of primitive units, which do not overlap and whose union equals the polygon. A polygon partition problem is a problem of finding a partition which is minimal in some sense, for example a partition with a smallest number of units or with units of smallest total side-length.

In computational geometry, a greedy geometric spanner is an undirected graph whose distances approximate the Euclidean distances among a finite set of points in a Euclidean space. The vertices of the graph represent these points. The edges of the spanner are selected by a greedy algorithm that includes an edge whenever its two endpoints are not connected by a short path of shorter edges. The greedy spanner was first described in the PhD thesis of Gautam Das and conference paper and subsequent journal paper by Ingo Althöfer et al. These sources also credited Marshall Bern (unpublished) with the independent discovery of the same construction.

Guillotine partition is the process of partitioning a rectilinear polygon, possibly containing some holes, into rectangles, using only guillotine-cuts. A guillotine-cut is a straight bisecting line going from one edge of an existing polygon to the opposite edge, similarly to a paper guillotine.








































